Phương trình bậc 3 có 1 nghiệm : Phương pháp và bước đầu tiên để giải quyết

Để phương trình bậc 3 có 1 nghiệm duy nhất, chúng ta cần kiểm tra hai điều kiện sau:
1. Điều kiện cần: Phương trình bậc 3 phải có dạng ax^3 + bx^2 + cx + d = 0, trong đó hệ số a khác 0.
2. Điều kiện đủ: Đạo hàm của hàm số đa thức T(x) = ax^3 + bx^2 + cx + d (tức f \'(x)) phải luôn dương trên một khoảng xác định.
Để tính đạo hàm của T(x), chúng ta thực hiện các bước sau:
- Tính đạo hàm của từng thành phần của đa thức theo quy tắc phái đạo:
+ Đạo hàm của ax^3 là 3ax^2.
+ Đạo hàm của bx^2 là 2bx.
+ Đạo hàm của cx là c.
- Viết phương trình đạo hàm: T\'(x) = 3ax^2 + 2bx + c.
Sau đó, kiểm tra giá trị của T\'(x) để xác định xem nó có dương trên một khoảng xác định hay không. Nếu T\'(x) luôn dương trên một khoảng xác định, thì phương trình bậc 3 sẽ có 1 nghiệm duy nhất.
Nếu điều kiện cần và điều kiện đủ đều được thỏa mãn, ta có thể kết luận rằng phương trình bậc 3 có duy nhất một nghiệm.

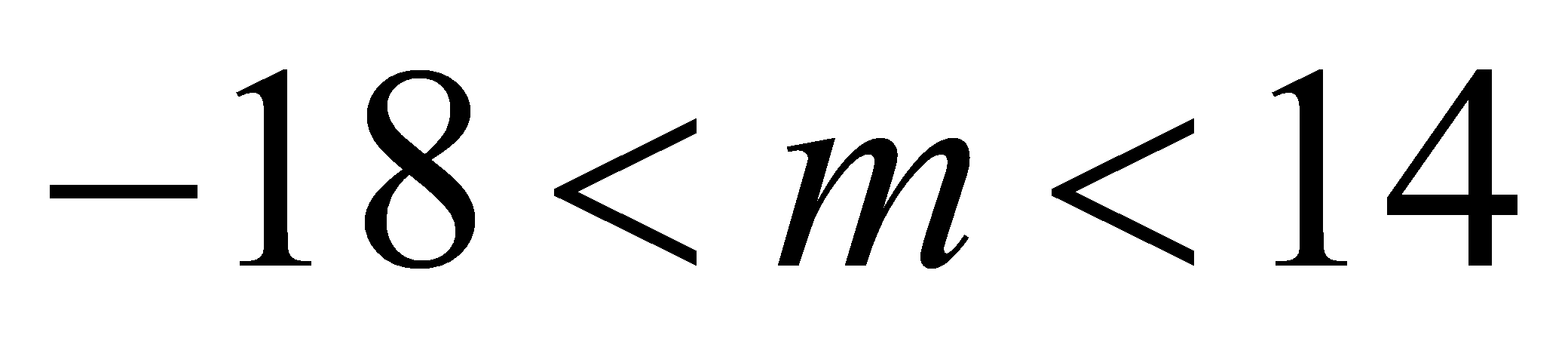
Phương trình bậc 3 có 1 nghiệm khi nào? Để giải phương trình bậc 3 có 1 nghiệm, ta cần thực hiện các bước sau:
Bước 1: Viết phương trình bậc 3 dưới dạng f(x) = ax^3 + bx^2 + cx + d = 0, với a, b, c, d là các hệ số xác định.
Bước 2: Tính đạo hàm của hàm số f(x) theo x và viết phương trình f\'(x) = 0.
Bước 3: Giải phương trình f\'(x) = 0 để tìm các giá trị của x.
Bước 4: Kiểm tra các giá trị của x thu được trong bước 3 bằng cách thay vào phương trình ban đầu f(x) = 0.
Nếu có 1 giá trị của x thỏa mãn phương trình ban đầu và đạo hàm bằng 0, tức là f\'(x) = 0, thì phương trình bậc 3 có duy nhất 1 nghiệm.
Tuy nhiên, giải phương trình bậc 3 có 1 nghiệm là một vấn đề phức tạp trong giải tích đại số và đôi khi không có giải pháp.

Để viết một phương trình bậc 3 dưới dạng f(x) = x^3 + ax^2 + bx + c, ta cần làm như sau:
Bước 1: Viết các hệ số của đa thức theo thứ tự giảm dần của mũ.
Bước 2: Xác định giá trị của a, b, c tùy thuộc vào những thông tin đã cho. Điều này có thể được mô tả thông qua ví dụ hoặc các điều kiện cụ thể.
Ví dụ: Nếu đã biết rằng phương trình bậc 3 có một nghiệm duy nhất là x = 2, ta có thể sử dụng thông tin này để xác định giá trị của a, b, c.
- Đầu tiên, ta sử dụng giá trị x = 2 vào phương trình f(x) để tạo thành một phương trình có cả hai phía bằng nhau: f(2) = 2^3 + a(2)^2 + b(2) + c = 0.
- Tiếp theo, ta giải phương trình này theo a, b, c. Kết quả cuối cùng sẽ cho ta phương trình bậc 3 dưới dạng f(x) = x^3 + ax^2 + bx + c.
Lưu ý rằng các bước trong việc viết một phương trình bậc 3 có thể khác nhau tùy thuộc vào thông tin đã cho và yêu cầu cụ thể của bài toán. Tuy nhiên, ý tưởng chính là xác định các hệ số theo thứ tự giảm dần của mũ và sử dụng thông tin có sẵn để tìm ra giá trị của chúng.

Điều kiện để một phương trình bậc 3 có nghiệm duy nhất là đạo hàm của đa thức đại diện cho phương trình đó phải lớn hơn 0 trên một khoảng xác định. Cụ thể, giả sử phương trình bậc 3 có dạng ax^3 + bx^2 + cx + d = 0, đạo hàm của đa thức này là T\'(x) = 3ax^2 + 2bx + c.
Điều kiện để phương trình bậc 3 có nghiệm duy nhất là đạo hàm của đa thức này phải lớn hơn 0 trên một khoảng xác định. Nghĩa là, đối với mọi giá trị x trong khoảng, đạo hàm của đa thức phải lớn hơn 0.
Để tìm khoảng này, ta cần giải phương trình T\'(x) = 0. Từ đó, ta có một số nghiệm x1, x2, x3 (có thể là thực hoặc phức) và chia khoảng giữa các nghiệm này thành các khoảng con. Sau đó, ta cần xác định dấu của đạo hàm trong từng khoảng con này. Nếu đạo hàm luôn lớn hơn 0 trên mỗi khoảng con, thì phương trình bậc 3 sẽ có nghiệm duy nhất.
Nếu có ít hơn hoặc nhiều hơn một khoảng con mà đạo hàm lớn hơn 0, thì phương trình bậc 3 sẽ có nhiều hơn một nghiệm. Nếu không có khoảng nào mà đạo hàm lớn hơn 0, thì phương trình bậc 3 sẽ không có nghiệm.
Tóm lại, để phương trình bậc 3 có nghiệm duy nhất, ta cần kiểm tra điều kiện đạo hàm của đa thức đại diện cho phương trình đó có lớn hơn 0 trên một khoảng xác định hay không.

Đạo hàm của một hàm số là khái niệm trong giải tích, được tính bằng cách lấy đạo hàm của hàm số đó theo biến số. Đạo hàm cho ta biết về tốc độ thay đổi của hàm số tại mỗi điểm và hướng của đường tiếp tuyến tại điểm đó. Đạo hàm còn được hiểu là độ dốc của đường cong biểu diễn hàm số tại một điểm.
Công thức tổng quát để tính đạo hàm của một hàm số là lấy đạo hàm theo biến số đó (thông thường là x) của từng thành phần của hàm số và cố định lại các hằng số. Đạo hàm của hàm số f(x) thường được ký hiệu là f\'(x) hoặc dy/dx.
Ví dụ, để tính đạo hàm của hàm số f(x) = x^2 + 3x, ta lấy đạo hàm của từng thành phần:
- Đạo hàm của x^2 là 2x.
- Đạo hàm của 3x là 3.
Vậy, đạo hàm của hàm số f(x) = x^2 + 3x là f\'(x) = 2x + 3.
Tuy nhiên, khi tính đạo hàm của một hàm số phức tạp hơn, chúng ta cần áp dụng các quy tắc của đạo hàm như quy tắc của đạo hàm tổng, đạo hàm tích, đạo hàm hàm hợp, và quy tắc xấp xỉ cao hơn (như đạo hàm số hữu tỉ, đạo hàm chuỗi,...).
Đạo hàm là một khái niệm quan trọng trong toán học và có ứng dụng rộng rãi trong nhiều lĩnh vực như vật lý, kỹ thuật, kinh tế, và xác suất thống kê.

Để tính đạo hàm của một hàm số bậc 3, ta cần làm theo các bước sau:
Bước 1: Viết hàm số bậc 3 dưới dạng f(x) = x^3 + ax^2 + bx + c
Bước 2: Tính đạo hàm của hàm số f(x) theo x
f\'(x) = 3x^2 + 2ax + b
Bước 3: Kiểm tra kết quả và thực hiện bước tiếp theo nếu cần
Đây là phương trình đạo hàm của hàm số bậc 3. Bạn có thể áp dụng nguyên tắc tính đạo hàm thông qua các công thức có sẵn.

3 có 1 nghiệm duy nhất.
Ý nghĩa của phương trình f\'(x) = 0 trong việc tìm nghiệm của phương trình bậc 3 là đó là điều kiện cần để xác định nghiệm duy nhất của phương trình bậc 3.
Đầu tiên, chúng ta biết rằng nghiệm của phương trình bậc 3 là giá trị của x mà khi thay vào phương trình sẽ làm cho cả phương trình trở thành một câu lời giống nhau.
Để tìm nghiệm của phương trình bậc 3, chúng ta thường sử dụng phương pháp dùng đạo hàm. Bước đầu tiên là viết hàm số bậc 3 dưới dạng f(x) = x^3 + ax^2 + bx + c. Tiếp theo, chúng ta tính đạo hàm của hàm số f(x) theo x, ký hiệu là f\'(x).
Phương trình f\'(x) = 0 là phương trình đạo hàm của hàm số f(x). Lời giải của phương trình này sẽ cho ta giá trị của x mà khi thay vào hàm số f(x), đạo hàm f\'(x) sẽ bằng 0. Điều này chính là điểm cực đại và cực tiểu của hàm số f(x) và là điểm mà giá trị của f(x) đạt cực đại hoặc cực tiểu.
Trong trường hợp phương trình bậc 3 có 1 nghiệm duy nhất, điểm cực đại hoặc cực tiểu của hàm số f(x) sẽ xác định giá trị của nghiệm của phương trình đó.
Vậy, ta có thể sử dụng phương trình f\'(x) = 0 để tìm nghiệm duy nhất của phương trình bậc 3.

Để giải phương trình bậc 3 có 1 nghiệm, chúng ta cần áp dụng các kiến thức của giải tích đại số. Dưới đây là các bước chi tiết để giải phương trình này:
Bước 1: Viết phương trình bậc 3 dưới dạng ax^3 + bx^2 + cx + d = 0. Đảm bảo rằng hệ số a khác không.
Bước 2: Tính đạo hàm của phương trình f(x) theo x. Đạo hàm f\'(x) = 3ax^2 + 2bx + c.
Bước 3: Đặt f\'(x) = 0 và giải phương trình này để tìm các nghiệm của f\'(x). Điều này giúp xác định các điểm uốn (điểm đổi dấu của đạo hàm) trong đồ thị của hàm số.
Bước 4: Kiểm tra các điểm uốn để xác định số lượng và vị trí của nghiệm của phương trình ban đầu.
- Nếu có một điểm uốn và f\'(x) không bằng không tại điểm đó (f\'(x) > 0 hoặc f\'(x) 0), thì phương trình bậc 3 có duy nhất một nghiệm.
- Nếu không có điểm uốn hoặc f\'(x) = 0 tại tất cả các điểm uốn, thì phương trình bậc 3 không có nghiệm hoặc có nhiều hơn một nghiệm.
Bước 5: Nếu phương trình có một nghiệm, ta có thể sử dụng các phương pháp như phân tích theo thừa số, đồ thị hàm số hoặc phương pháp Newton–Raphson để tìm giá trị cụ thể của nghiệm.
Để giải phương trình bậc 3 có 1 nghiệm, việc nắm vững các kiến thức về giải tích đại số là rất quan trọng. Bạn có thể tham khảo thêm tài liệu và bài giảng về chủ đề này để nắm vững và áp dụng hiệu quả vào việc giải các phương trình tương tự.

Phương trình bậc 3 có 1 nghiệm duy nhất là một vấn đề khá phức tạp trong giải tích đại số. Để giải phương trình bậc 3 này, chúng ta có thể sử dụng phương pháp công thức không gian làm việc, cũng như sử dụng đa thức đặt biệt (ví dụ: đa thức Chebyshev hoặc đa thức Legendre) để áp dụng các thuật toán giải phương trình.
Cụ thể, để giải phương trình bậc 3 có 1 nghiệm, ta có thể thực hiện các bước sau:
Bước 1: Viết phương trình bậc 3 dưới dạng f(x) = 0. Ví dụ: ax^3 + bx^2 + cx + d = 0
Bước 2: Tính đạo hàm của hàm số f(x) theo x. Phương trình f\'(x) = 0 được gọi là phương trình đạo hàm.
Bước 3: Xác định nghiệm của phương trình đạo hàm. Nếu phương trình đạo hàm có một nghiệm duy nhất, chúng ta có thể áp dụng các phương pháp giải phương trình bậc 2 để tìm nghiệm của phương trình bậc 3.
Bước 4: Kiểm tra điều kiện dT/dx > 0 để đảm bảo rằng phương trình bậc 3 có một nghiệm duy nhất. Điều kiện này đảm bảo rằng đồ thị của hàm số có đặc tính tăng hoặc giảm đối với giá trị của x trong vùng xác định.
Việc giải phương trình bậc 3 có 1 nghiệm có thể trở nên rất phức tạp và đòi hỏi sự chính xác và cẩn thận. Việc sử dụng công thức không gian làm việc hoặc các đa thức đặt biệt có thể giúp giảm thiểu sự phức tạp và tăng độ chính xác trong việc giải phương trình này.

Phương trình bậc 3 có 1 nghiệm được xem như một vấn đề quan trọng trong giải tích đại số vì nó đòi hỏi phương pháp giải cụ thể và khá phức tạp. Để hiểu tại sao vấn đề này quan trọng, ta cần xem xét các bước giải phương trình bậc 3.
Bước đầu tiên trong việc giải phương trình bậc 3 là đưa phương trình về dạng chuẩn ax^3 + bx^2 + cx + d = 0. Sau đó, ta phải tìm cách tìm nghiệm của phương trình này.
Để giải phương trình bậc 3, ta có thể áp dụng nhiều phương pháp như phương pháp Viết trì hoãn, phương pháp Trạng thái đoán, phương pháp Phân rã thành phương trình nhỏ hơn. Mỗi phương pháp đều có ưu điểm và hạn chế riêng, và đòi hỏi kiến thức sâu về giải tích và đại số để áp dụng.
Sau khi áp dụng phương pháp phù hợp, ta có thể tìm được 1 nghiệm duy nhất cho phương trình bậc 3. Việc tìm ra nghiệm duy nhất này có thể giúp ta hiểu rõ hơn về đặc điểm của hàm số và các hệ phương trình liên quan.
Tuy nhiên, quan trọng nhất là việc giải phương trình bậc 3 đóng vai trò quan trọng trong các lĩnh vực như vật lý, kỹ thuật, kinh tế và nhiều lĩnh vực khác, nơi tính toán và đánh giá các điều kiện phụ thuộc vào giá trị của x. Việc tìm ra nghiệm duy nhất của phương trình bậc 3 có thể giúp ta hiểu rõ hơn về quan hệ giữa các biến số và giải quyết các vấn đề trong thực tế.
Tóm lại, việc giải phương trình bậc 3 có 1 nghiệm được coi là vấn đề quan trọng trong giải tích đại số vì nó đòi hỏi sự thông thạo về các phương pháp giải và cung cấp cơ sở để hiểu và ứng dụng các quy luật toán học vào thực tế.