Chủ đề Công thức tính chu vi diện tích hình tam giác: Công thức tính chu vi và diện tích của hình tam giác là rất quan trọng và hữu ích để giúp chúng ta giải quyết một số bài toán liên quan đến hình tam giác. Với công thức p = a + b + c, ta có thể tính chu vi của hình tam giác dễ dàng. Còn với công thức S = 0.5 * h * a (với h là chiều cao và a là độ dài cạnh đối diện), chúng ta có thể tính diện tích của hình tam giác một cách nhanh chóng.
Cách tính chu vi và diện tích của hình tam giác?
Cách tính chu vi của hình tam giác là cộng độ dài của 3 cạnh lại với nhau.
Ví dụ, cho hình tam giác có độ dài các cạnh lần lượt là a, b và c, ta có công thức để tính chu vi là P = a + b + c.
Cách tính diện tích của hình tam giác là nhân chiều cao của tam giác với nửa chu vi rồi chia cho 2.
Ví dụ, cho hình tam giác có chiều cao h, ta có công thức để tính diện tích là S = (1/2) * h * P, trong đó P là chu vi của tam giác.
Nếu không có chiều cao h của tam giác, ta có thể sử dụng công thức Heron để tính diện tích. Công thức Heron là S = √(p * (p - a) * (p - b) * (p - c)), với p = (a + b + c) / 2 là nửa chu vi của tam giác.
Tuy nhiên, nếu có thông tin về độ dài chiều cao hoặc độ dài các cạnh của tam giác, ta có thể áp dụng các công thức tương ứng để tính chu vi và diện tích.
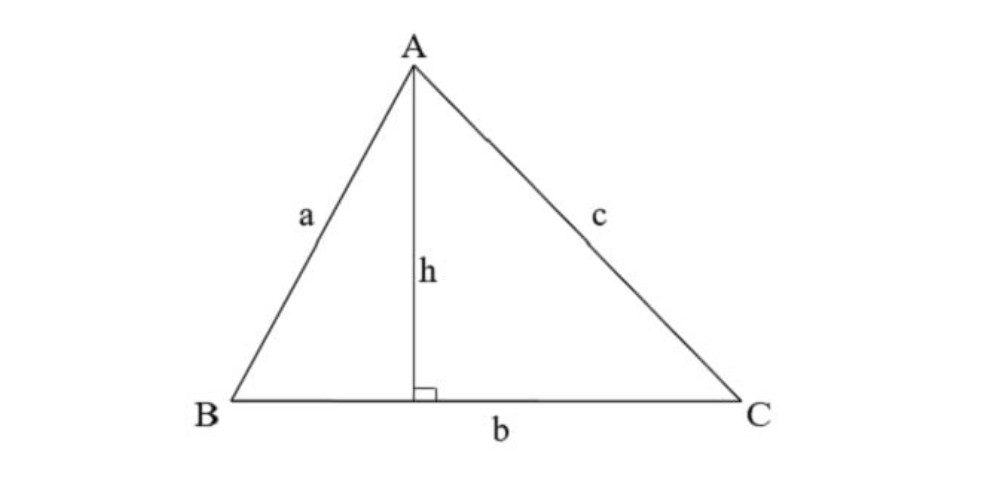
Công thức nào được sử dụng để tính chu vi của một hình tam giác?
Công thức được sử dụng để tính chu vi của một hình tam giác là tổng độ dài của ba cạnh. Khi biết độ dài của ba cạnh là a, b, và c, ta tính tổng ba cạnh này bằng cách thực hiện phép cộng a + b + c. Vậy công thức để tính chu vi của một hình tam giác là P = a + b + c.
Làm thế nào để tính diện tích của một hình tam giác?
Để tính diện tích của một hình tam giác, chúng ta có thể sử dụng công thức sau:
S = ½ × b × h
Trong đó S là diện tích của tam giác, b là độ dài một cạnh của tam giác và h là độ dài đường cao kẻ từ đỉnh của tam giác xuống đối diện với cạnh tương ứng.
Cách tính diện tích cho từng loại tam giác:
1. Tam giác vuông: Trong tam giác vuông, chúng ta thường biết độ dài hai cạnh góc vuông (a, b). Để tính diện tích, ta chỉ cần nhân độ dài của hai cạnh góc vuông và chia cho 2:
S = ½ × a × b
2. Tam giác tổng quát: Trong tam giác tổng quát, chúng ta có thể sử dụng độ dài hai cạnh bất kỳ và độ dài góc giữa chúng, hoặc cạnh và đường cao kẻ từ cạnh đó.
a) Sử dụng độ dài hai cạnh: Chúng ta có thể áp dụng công thức Heron để tính diện tích:
p = ½ × (a + b + c)
Trong đó p là nửa chu vi của tam giác. Sau đó, áp dụng công thức sau để tính diện tích:
S = √(p × (p - a) × (p - b) × (p - c))
Trong đó a, b, c lần lượt là các cạnh của tam giác.
b) Sử dụng cạnh và đường cao: Nếu chúng ta biết độ dài cạnh và độ dài đường cao kẻ từ cạnh đó, ta có thể tính diện tích bằng công thức:
S = ½ × b × h
Trong đó b là độ dài cạnh và h là đường cao tương ứng.
Ví dụ: Giả sử chúng ta có một tam giác có cạnh a = 5 cm và đường cao h = 3 cm. Chúng ta có thể tính diện tích như sau:
S = ½ × 5 cm × 3 cm = 7.5 cm²
Vậy diện tích của tam giác đó là 7.5 cm².

Cách tính chu vi và diện tích hình tam giác
Muốn tìm hiểu cách tính chu vi và diện tích tam giác? Video này sẽ giúp bạn hiểu rõ về công thức và cách ứng dụng chúng vào bài toán thực tế. Đừng bỏ lỡ cơ hội nâng cao kiến thức toán học của bạn, hãy xem ngay!
Tam giác là gì? Hãy cho một định nghĩa đơn giản.
Tam giác là một hình học được tạo thành bởi ba đoạn thẳng nối ba điểm không thẳng hàng trên mặt phẳng. Tam giác có ba đỉnh, ba cạnh và ba góc. Cạnh tam giác là đoạn thẳng nối hai đỉnh của tam giác. Góc tam giác là không gian giữa hai đoạn thẳng nằm trên hai đỉnh của tam giác. Tam giác là một trong những hình học căn bản và có nhiều tính chất hấp dẫn. Đối với tam giác, có rất nhiều công thức và cách tính chu vi, diện tích mà ta có thể sử dụng để giải quyết các bài toán liên quan.
Có bao nhiêu công thức khác nhau để tính diện tích hình tam giác?
Có nhiều công thức khác nhau để tính diện tích của hình tam giác. Dưới đây là một số công thức phổ biến được sử dụng:
1. Công thức diện tích tam giác vuông: S = 1/2 * a * b
Trong đó, a và b là độ dài hai cạnh góc vuông của tam giác, và S là diện tích tam giác.
2. Công thức diện tích tam giác bằng nửa tích vô hướng của hai vector: S = 1/2 * |AB x AC|
Trong công thức này, AB và AC là hai vector tạo thành hai cạnh tam giác, và |AB x AC| là độ dài tích vô hướng của hai vector này.
3. Công thức diện tích tam giác bằng bán kính ngoại tiếp và ba cạnh tam giác: S = r * (a + b + c) / 2
Trong công thức này, r là bán kính đường tròn ngoại tiếp tam giác, a, b và c là độ dài ba cạnh của tam giác.
4. Công thức diện tích tam giác bằng phép chia: S = sqrt(p * (p - a) * (p - b) * (p - c))
Trong công thức này, p = (a + b + c) / 2 là nửa chu vi tam giác, và a, b, c là độ dài ba cạnh của tam giác.
Như vậy, có ít nhất 4 công thức khác nhau để tính diện tích của hình tam giác. Tuy nhiên, còn nhiều công thức khác nữa tùy thuộc vào thông tin cụ thể về tam giác và đối tượng cần tính.
_HOOK_
Tại sao cần phải đo chiều cao của tam giác để tính diện tích?
Chiều cao của tam giác là một trong những thành phần quan trọng để tính diện tích tam giác. Khi ta biết đường cao của tam giác, ta có thể sử dụng công thức tính diện tích tam giác bằng cách nhân chiều cao với độ dài cạnh đối diện rồi chia cho 2.
Công thức tính diện tích tam giác theo chiều cao là:
Diện tích tam giác = (Chiều cao tam giác x Độ dài cạnh đối diện)/2
Việc đo chiều cao tam giác giúp xác định độ dài đường thẳng từ đỉnh của tam giác đến cạnh đối diện và tạo thành đường vuông góc với cạnh đối diện. Chiều cao là một đường thẳng tạo ra hai tam giác vuông con nhỏ hơn, và việc tính diện tích của các tam giác con này dễ dàng hơn.
Do đó, việc đo chiều cao của tam giác rất quan trọng để tính diện tích tam giác theo công thức trên.
Công thức tính chu vi và diện tích hình tam giác vuông
Bạn muốn biết cách tính chu vi và diện tích của tam giác vuông? Đừng lo, video này sẽ hướng dẫn bạn từng bước một, dễ hiểu và chi tiết. Cùng lắng nghe giảng viên giải thích và xem ví dụ minh họa để trở thành chuyên gia tính toán tam giác vuông!
Có cách tính chu vi nào khác không nếu biết độ dài ba cạnh của tam giác?
Nếu biết độ dài ba cạnh của tam giác, ta cũng có thể tính chu vi bằng cách cộng tổng độ dài ba cạnh lại với nhau. Cách tính này khá đơn giản và không cần sử dụng công thức riêng biệt. Ta chỉ cần lấy độ dài cạnh thứ nhất cộng với độ dài cạnh thứ hai, rồi cộng thêm với độ dài cạnh thứ ba.
Ví dụ, giả sử ta có tam giác ABC với độ dài ba cạnh lần lượt là a, b và c. Ta có thể tính chu vi P bằng cách sử dụng công thức P = a + b + c.
Vậy, ngoài cách sử dụng công thức P = a + b + c, ta cũng có thể tính chu vi tam giác khi biết độ dài ba cạnh bằng cách cộng tổng độ dài ba cạnh lại với nhau.
.jpg)
Làm thế nào để tính độ dài cạnh của tam giác nếu biết chu vi và các thông số khác?
Để tính độ dài cạnh của tam giác khi biết chu vi và các thông số khác, ta có thể sử dụng công thức sau:
1. Đầu tiên, ta cần biết công thức tính chu vi tam giác. Chu vi tam giác bằng tổng độ dài của ba cạnh của tam giác. Ta có công thức:
P = a + b + c
Trong đó P là chu vi tam giác, a, b, c là độ dài của ba cạnh của tam giác.
2. Tiếp theo, ta cần xem xét các thông số khác như đường cao, bán kính đường tròn ngoại tiếp, diện tích tam giác để áp dụng các công thức liên quan.
3. Nếu biết đường cao h, ta có thể sử dụng công thức tính diện tích tam giác:
S = (1/2) * a * h
Trong đó S là diện tích tam giác, a là độ dài cạnh của tam giác, h là độ dài đường cao của tam giác kẻ từ cạnh tương ứng với đường cao.
4. Nếu biết diện tích tam giác S, ta có thể sử dụng công thức tính diện tích tam giác:
S = (a * b * c) / 4R
Trong đó S là diện tích tam giác, a, b, c là độ dài của ba cạnh của tam giác, R là bán kính đường tròn ngoại tiếp tam giác.
Tóm lại, để tính độ dài cạnh của tam giác khi biết chu vi và các thông số khác, ta cần sử dụng các công thức liên quan như công thức tính chu vi tam giác, công thức tính diện tích tam giác, công thức tính đường cao và công thức tính bán kính đường tròn ngoại tiếp tam giác. Sử dụng những thông số đã biết và áp dụng các công thức tương ứng, ta có thể tính được độ dài cạnh của tam giác.
Trong việc tính diện tích tam giác, giá trị nào được sử dụng để đại diện cho chu vi?
Trong việc tính diện tích tam giác, giá trị chu vi được sử dụng để đại diện cho tam giác đó là \"P\" (P là biểu diễn cho chu vi tam giác).
Có tồn tại một công thức tổng quát nào để tính chu vi và diện tích của mọi tam giác không?
Có, tồn tại một công thức tổng quát để tính chu vi và diện tích của mọi tam giác. Dưới đây là cách tính chu vi và diện tích của một tam giác:
1. Chu vi tam giác:
- Gọi a, b và c là độ dài của 3 cạnh tam giác.
- Tính tổng a + b + c để được chu vi tam giác.
2. Diện tích tam giác:
- Gọi a, b và c là độ dài của 3 cạnh tam giác.
- Tính nửa chu vi tam giác bằng công thức p = (a + b + c) / 2.
- Sử dụng công thức diện tích tam giác Heron để tính diện tích tam giác: S = sqrt(p * (p - a) * (p - b) * (p - c)), trong đó sqrt là dấu căn bậc hai.
Lưu ý rằng công thức này chỉ áp dụng cho tam giác có bất kỳ hình dạng nào, bao gồm cả tam giác vuông, tam giác đều và tam giác không đều.
_HOOK_











