Bí quyết tính thể tích hình trụ sẽ được Mytour cập nhật trong bài viết này, giúp bạn nhanh chóng nắm bắt kiến thức, làm cho công việc và học tập trở nên dễ dàng hơn.
Chắc hẳn bạn đã biết đến hình trụ tròn, một hình có hai mặt đáy là hai hình tròn song song và bằng nhau. Có nhiều đồ vật hình trụ như lon sữa, cái cốc, lọ hoa, thùng, xô,... Cách tính thể tích hình trụ không chỉ đơn giản mà còn có nhiều ứng dụng thực tế. Hãy cùng tìm hiểu công thức tính thể tích hình trụ nhé.
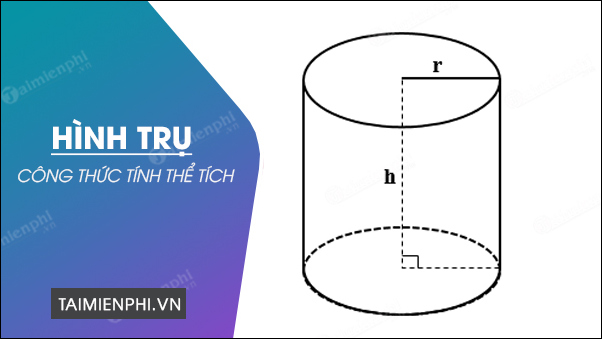
Cách tính thể tích hình trụ tròn và một số bài tập thú vị để ôn tập
I. Bí quyết tính thể tích hình trụ
- Để tính thể tích của hình trụ tròn, sử dụng công thức:V = π. r2. h
Cụ thể:
- V là ký hiệu thể tích
- r là bán kính đáy hình trụ
- h là chiều cao của hình trụ
- π là hằng số ( π = 3,14)
- Đơn vị thể tích: mét khối (m3)
- Phát biểu: Để tính thể tích của hình trụ, nhân chiều cao với bình phương bán kính hình tròn mặt đáy và số pi.
Ví dụ minh họa: Tính thể tích của hình trụ khi bán kính đáy bằng 7,1 cm và chiều cao bằng 5 cm.
Hướng dẫn giải bài tập: Áp dụng công thức tính thể tích khối trụ, thay vào số và tính toán. Kết quả: 3.14 x (7,1)2 x 5 = 791,437 (cm3)
Áp dụng công thức tính thể tích khối trụ để giải bài tập về thể tích hình trụ tròn, thể tích hình trụ ngoại tiếp hình lập phương cạnh a, thể tích hình trụ có bán kính đáy bằng a nội tiếp mặt cầu bán kính 2a,...
II. Bí quyết xác định các giá trị trong bài toán tính thể tích hình trụ
1. Xác định bán kính đáy
- Cách đo bán kính đáy: Chọn bất kỳ mặt đáy nào vì cả hai đều giống nhau. Trong trường hợp chưa biết bán kính, sử dụng thước để đo đường kính và chia cho 2 (r = 1/2.d). Ví dụ: Nếu đo được 5 cm, thì bán kính là 2,5 cm.
* Chú ý: Đường kính là dây cung lớn nhất của hình tròn. Khi đo đường kính, chọn một mép nằm ở điểm số 0 của thước, đo độ dài lớn nhất mà không làm mốc số 0 di chuyển để tìm độ dài đường kính.
2. Tính diện tích đáy tròn
- Để tính diện tích đáy tròn, sử dụng công thức: A = π.r2 với A là diện tích đáy tròn, r là bán kính mặt đáy hình trụ. Ví dụ: Diện tích đáy tròn khi r = 6,5 cm là: 3,14 x (6,5)2 = 132, 665 (cm2)
3. Xác định chiều cao của hình trụ
- Chiều cao hình trụ là khoảng cách giữa hai đáy trên mặt bên.
- Nếu chưa biết chiều cao, sử dụng thước để đo chính xác độ dài đường cao và thay vào công thức để tính thể tích hình trụ.
Cách tính thể tích hình trụ và áp dụng vào giải bài tập là một quá trình dễ hiểu và nhớ. Hãy nắm vững để giải các bài toán đơn giản. Tham khảo thêm bài tập thể tích hình trụ nâng cao và công thức diện tích trên Mytour. Nếu có cách giải hay, chia sẻ để giải bài toán nhanh chóng hơn. Mong rằng bạn sẽ luôn yêu thích Toán học và Hình học.
III. Ví dụ Giải Bài tập về diện tích, thể tích hình trụ trong SGK
1. Giải bài 6 Toán 9 tập 2 SGK trang 111
Chiều cao hình trụ bằng bán kính đường tròn đáy. Diện tích xung quanh hình trụ 314 cm2. Tính bán kính và thể tích hình trụ (làm tròn đến chữ số thập phân thứ hai).
Bước hướng dẫn giải
Diện tích xung quanh hình trụ là 314cm2
⇔ 2.π.r.h = 314
Với r = h
Vì vậy, 2πr2 = 314
⇒ r2 ≈ 50
⇒ r ≈ 7,07 (cm)
Thể tích hình trụ là: V = π.r2.h = π.r3 ≈ 1109,65 (cm3).
2. Giải Bài 10 Toán 9 Tập 2 SGK trang 112
Tính:
a) Diện tích xung quanh của hình trụ có chu vi đáy là 13cm và chiều cao là 3cm.
b) Thể tích của hình trụ có bán kính đáy là 5mm và chiều cao là 8mm.
Bước hướng dẫn giải
a) Cho: C = 13cm, h = 3cm
Diện tích xung quanh của hình trụ:
Sxq = 2πr.h = C.h = 13.3 = 39 (cm2)
b) Cho: r = 5mm, h = 8mm
Thể tích hình trụ là:
V = πr2.h = π. 52.8 = 200π ≈ 628 (mm3)
3. Bài 11 trang 112 SGK Toán 9 Tập 2
Người ta nhấn chìm hoàn toàn một tượng đá nhỏ vào lọ thủy tinh hình trụ (h.84).
Diện tích đáy lọ thủy tinh là 12,8cm2. Nước trong lọ dâng lên thêm 8,5mm. Hỏi thể tích của tượng đá là bao nhiêu?
Bước hướng dẫn giải
Thể tích tượng đá bằng thể tích hình trụ, diện tích đáy 12,8cm2, chiều cao 0,85cm:
V = S.h = 12,8 . 0,85 = 10,88 (cm3)
=> Xem thêm hướng dẫn Giải bài tập trang 110, 111 SGK Toán 9 Tập 2 để hiểu cách làm, vận dụng công thức thể tích trong giải bài.
""""--HẾT""""--
Các em cũng cần ôn lại và nắm vững cách tính diện tích hình tròn trong hình học phẳng, là kiến thức cơ bản để giải bài toán liên quan đến hình tròn.
Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc và tăng trải nghiệm khách hàng. Mọi ý kiến đóng góp xin vui lòng liên hệ tổng đài chăm sóc: 1900 2083 hoặc email: [email protected]











