Nhiều học sinh gặp khó khăn với phần kiến thức Toán học trung học phổ thông công thức cấp số nhân . Vậy cấp số nhân là gì và tính chất như thế nào? Công thức cấp số nhân đầy đủ và các bài tập tương quan đã được The Dewey Schools tổng hợp ngay lập tức nhập nội dung dưới phía trên. Các em học sinh hãy tham ô khảo ngay lập tức để kịp thời bổ sung những kiến thức cần thiết mang lại mình nhé.
Cập nhật kỹ năng và kiến thức công thức cấp số nhân khá đầy đủ nhất 1. Định nghĩa cấp số nhân Định nghĩa: Cấp số nhân là dãy số vô hạn hoặc hữu hạn thỏa mãn điều kiện: kể từ số hạng thứ 2 , mỗi số là tích của số hạng đứng ngay lập tức trước đó và 1 số cố định gọi là hằng số. Hằng số này được gọi là công bội của cấp số nhân ký hiệu là q.
Bạn đang xem: Cấp số nhân là gì? Cập nhật kiến thức công thức cấp số nhân đầy đủ nhất
Công thức tính cấp số nhân: Un+1 = Un . q (n ∈ N*)
Trong đó:
Un: cấp số nhân q: công bội n ∈ N*
Ví dụ: Cho dãy số 1, 3, 9, 27, 81, 243, 729… phía trên là cấp số nhân phần tử đầu tiên là U1 = 1, công bội q = 3
Xem thêm: Tuyển tập kiến thức công thức lượng giác lớp 10 đầy đủ nhất
2. Tính chất của cấp số nhân Cấp số nhân có một số tính chất sau:
Tính chất 1 : Nếu Un là 1 cấp số nhân thì từ số hạng thứ 2, bình phương của mỗi số hạng (trừ số hạng cuối cùng với cấp số nhân hữu hạn) bằng tích của số đứng sau và đứng trước liền kề.
Công thức: (Uk) 2 = Uk-1 . Uk+1
Ví dụ:
Cho cấp số nhân (Un) nhập đó U3 = 4, U5 = 16. Tìm U4 của cấp số nhân?
Đáp án:
Áp dụng công thức: (Uk) 2 = Uk-1 . Uk+1
=> U4 2 = U3 . U5
=> U4 2 = 4 . 16
=> U4 = 8
Vậy U4 của cấp số nhân là 8
Xem thêm: Cập nhật kiến thức tổng hợp về số hữu tỉ mới nhất 2023
Tính chất 2: Công bội đặc biệt
Nếu q = 0: cấp số nhân có dạng U1, 0, 0, 0, 0, 0… Nếu q = 1: cấp số nhân có dạng U1, U1, U1, U1, U1… Nếu q < 0: cấp số nhân là dãy số ko giảm, ko tăng Nếu q < 1 và q > 0: cấp số nhân (Un) là dãy số giảm Nếu q > 1: cấp số nhân (Un) là dãy số tăng Nếu U1 = 0: cấp số nhân có dạng 0, 0 ,0 ,0 ,0, 0…
Cập nhật kiến thức các công thức cấp số nhân lớp 11 Cập nhật kiến thức các công thức cấp số nhân lớp 11 Cập nhật kiến thức các công thức cấp số nhân lớp 11 đầy đủ nhất giúp học sinh tổng hợp kiến thức. Từ đó suôn sẻ học thuộc cũng như áp dụng kiến thức vào giải các bài tập có tương quan. Ngay dưới phía trên hãy cùng The Dewey Schools tìm hiểu biết vấn đề chi tiết và ví dụ về 5 công thức cấp số nhân các em học sinh nhé.
Xem thêm: [2023 Update] Tổng hợp ý công thức lượng giác lớp 10, 11
Xem thêm: Chi tiết các công thức Logarit lớp 12 chuẩn nhất 2023
1. Công thức truy hồi Cho Un là cấp số nhân thì công thức truy hồi là: Un = Un-1 . q (n ∈ N*)
Ví dụ:
Cho cấp số nhân (Un), nhập đó U2 = 9, q = 3. Tìm công thức truy hồi U4 của cấp số nhân?
Đáp án:
Theo đề bài tao có U2 = 9, q = 3
=> U3 = U2 . 3
=> U3 = 9 . 3
=> U3 = 27
Công thức truy hồi cấp số nhân (Un) là: Un = Un-1 . q
=> U4 = U3 . 3
=> U4 = 27 . 3
=> U4 = 81
2. Công thức tổng quát tháo cung cấp số nhân Nếu Un là cấp số nhân có số hạng đầu U1 và công bội q thì số hạng tổng quát Un được tính bằng công thức dưới đây:
Công thức tổng quát cấp số nhân (Un) = U1 . q n-1
Ví dụ:
Cho cấp số nhân (Un), nhập đó có U1 = 6, q = 3. Tính số hạng tổng quát U4?
Đáp án:
Áp dụng công thức: Un = U1 . q n-1
Số hạng tổng quát U4 của cấp số nhân là: U4 = 6 . 3 4-1
=> U4 = 162
Số hạng tổng quát U4 của cấp số nhân (Un) là 162
3. Công thức tính công bội q của cấp số nhân Công bội q của cấp số nhân (Un) được tính bằng công thức: q = (Un+1)/Un
Ví dụ 1:
Cho cấp số nhân có U1 = 5, U2 = đôi mươi. Tính công bội q?
Đáp án:
Áp dụng công thức q = (Un+1)/Un
=> q = U2/U1
=> q = 20/5
=> q = 4
Công bội của cấp số nhân có U1 = 5, U2 = đôi mươi là q = 4
Ví dụ 2:
Cho cấp số nhân có U5 = 7, U6 = 49. Tính công bội q?
Đáp án:
Áp dụng công thức q = (Un+1)/Un
=> q = U6/U5
=> q = 49/7
=> q = 7
Công bội của cấp số nhân có U5 = 7, U6 = 49 là q = 7
4. Công thức tính tổng n số hạng đầu tiên Cho cấp số nhân (Un) có công bội q ≠ 1, tao có công thức tổng n số hạng đầu tiên là:
Sn = U1 + U2 + U3 + U4 + U5 + … + Un
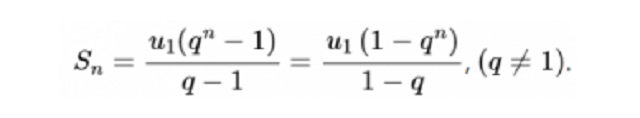
Ví dụ:
Cho cấp số nhân (Un) có U1 = 4, q = 3. Tính S5?
Đáp án:
Áp dụng công thức tính n số hạng đầu tiên tao có:
S5 = U1( 1- q 5 )/ (1 – q)
=> S5 = 4 (1 – 3 5 )/ (1 – 3)
=> S5 = 4 . (-242)/ (-2)
=> S5 = 484
Tổng của 5 số hạng đầu tiên S5 = 484
5. Công thức tính tổng của cấp số nhân lùi vô hạn Cấp số nhân lùi vô hạn Un có công bội q (1 < q < 1) là cấp số nhân lùi vô hạn
Công thức tính tổng của cấp số nhân lùi vô hạn S là:
Sn = U1 + U2 + U3 + U4 + … + Un + …
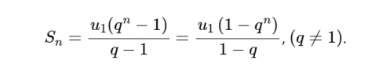
=> Sn = limSn
=> Sn = lim (U1 . (1 – q n )/ (1 – q)
=> Sn = U1/ (1-q)
Ví dụ:
Tính tổng của cấp số nhân lùi vô hạn Un có Un = 1/ 3 n
Đáp án:
Theo đề bài tao có Un = 1/ 3 n
=> U1 = ⅓
=> U2 = 1/9
=> Công bội q = U2/ U1 = 1/3
Áp dụng công thức: S = U1/ (1-q)
=> S = 1/3 : (1-⅓)
=> S = ½
Tổng của cấp số nhân lùi vô hạn có Un = 1/ 3 n là S = 1/2
Các dạng bài tập luyện tập kiến thức cấp số nhân Luyện tập kiến thức công thức cấp số nhân qua loa các dạng bài tập Rèn luyện liên tiếp các dạng bài tập về công thức tổng quát cấp số nhân là cách hiệu quả để ghi nhớ và hiểu biết rõ về nội dung kiến thức này. Vậy công thức tính cấp số nhân có các dạng bài tập cơ bản nào? The Dewey Schools đã tổng hợp một số dạng bài tập điển hình để các em học sinh thuận tiện tìm tài liệu và luyện tập.
Dạng 1: Nhân biết công thức CSN Phương pháp giải bài tập dạng 1:
Bước 1: Áp dụng công thức tính q = Un+1 / Un (n = 1, n>1) Bước 2: Kiểm tra và kết luận
Nếu q thay cho đổi thì Un ko phải là cấp số nhân
Nếu q ko đổi thì Un là cấp số nhân
Ví dụ 1:
Xem thêm: Tổng quan về ảnh hình trắng
Cho cấp số nhân (Un) có số hạng thứ 2 là 6, công bội q = 3. Viết 6 số hạng đầu tiên của cấp số nhân (Un)?
Đáp án:
Viết 6 số hạng đầu tiên của cấp số nhân (Un) có công bội q = 3, U2 = 6:
2, 6, 18, 54, 162, 486
Ví dụ 2:
Cho dãy số Un thỏa mãn điều kiện Un = 3 n+1 . Đây có phải là cấp số nhân không?
Đáp án:
Áp dụng công thức: q = (Un+1)/Un
=> q = 3 n+1+1 /3 n+1
=> q = 3
Vậy Un là cấp số nhân với U1 = 9, q = 3
Dạng 2: Tính công bội của cấp số nhân Phương pháp giải bài tập dạng 2:
Bước 1: Sử dụng các tính chất, công thức tính cấp số nhân Bước 2: Biến đổi tính chất, công thức tính cấp số nhân để tính công bội của cấp số nhân
Ví dụ 1:
Cho cấp số nhân (Un) có U2 = 3, U4 = 27. Tính công bội q của cấp số nhân?
Đáp án:
Áp dụng tính chất của cấp số nhân (Uk) 2 = Uk-1 . Uk+1
=> U3 2 = U2 . U4
=> U3 2 = 27 . 3
=> U3 = 9
Áp dụng công thức tính công bội q = U3/U2
=> q = 9/3
=> q = 3
Công bội của cấp số nhân (Un) là q = 3
Ví dụ 2: Cho 3 số a, b , c lập thành cấp số nhân và 3 số a, 2b, 3c là cấp số cộng. Tìm công bội q?
Đáp án:
Theo đề bài tao có 3 số a, 2b, 3c lập thành cấp số cộng => a + 3c = 4b
=> 3q 2 – 4q + 1 = 0 (a ≠ 0)
=> q = 1 hoặc q = 1/3
Công bội của cấp số nhân q = 1 hoặc q = ⅓
Dạng 3: Tính tổng cấp số nhân của các số hạng nhập dãy Phương pháp giải bài tập dạng 4:
Bước 1: Áp dụng công thức tính tổng cấp số nhân
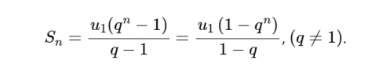
Bước 2: Tính tổng cấp số nhân của số hạng nhập dãy
Ví dụ 1:
Cho cấp số nhân (Un) nhập đó U3 = 2/9, U4 = 2/27
Tìm 5 số hạng đầu tiên của cấp số nhân (Un)? Tính tổng 10 số hạng đầu tiên của cấp số nhân (Un)?
Đáp án:
Tính công bội q = U4/u3
=> q = ⅓
Liệt kê 5 số hạng đầu tiên của cấp số nhân (Un) là: 2, 2/ 3, 2/9, 2/27, 2/81
Tính tổng 10 số hạng đầu tiên của cấp số nhân Un áp dụng công thức
S10 = U1 (q 2 – 1)/ (q – 1) => S10 = 2 ((⅓) 2 – 1)/ (1/3 – 1) => S10 = 59048/19683
Vậy tổng 10 số hạng đầu tiên của cấp số nhân (Un) là S10 = 59048/19683
Ví dụ 2:
Cho cấp số nhân (Un) nhập đó:
Tính S = U2 + U4 + U6 + U8 + … + U20
Đáp án:
Áp dụng công thức tính công bội q = Un+1 / Un
=>
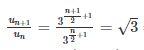
Dáy số U2, U4, U6, U8, …U20 lập thành cấp số nhân có số hạng đầu là U2 = 9, công bội q = 3
=> S = U2 + U4 + U6 + U8 + … + U20
=> S = U2 (1 – 3 10 ) / (1 – 3)
=> S = 9/2 . (3 10 – 1)
Vậy S = U2 + U4 + U6 + U8 + … + U20 = 9/2 . (3 10 – 1)
Dạng 4: Tìm số hạng bất kỳ của cấp số nhân Phương pháp giải bài tập dạng 4:
Bước 1: Áp dụng công thức tính số hạng tổng quát Un = U1 . q n-1
Bước 2: Tính số hạng bất kỳ của cấp số nhân
Ví dụ 1:
Cho cấp số nhân (Un) có U3 = 8, U4 = 16. Tìm U10 của cấp số nhân?
Đáp án:
Tính công bội q của cấp số nhân: q = U4/U3
=> q = 16/8
=> q = 2
Áp dụng công thức tính số hạng tổng quát: Un = U1 . q n-1
=> U10 = U3 . q 10-3
=> U10 = 8 . 2 7
=> U10 = 1024
Số hạng thứ 10 của cấp số nhân (Un) là 1024
Ví dụ 2:
Tính U1 và công bội q của cấp số nhân (Un) biết: U4 – U2 = 72 và U5 – U3 = 144
Đáp án:
Từ dữ liệu đề bài tao có:
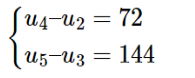
Ta biến đổi:
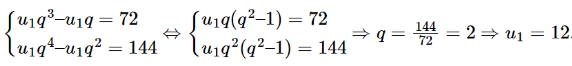
Vậy cấp số nhân (Un) có U1 = 12, cấp số nhân q = 2
Dạng 5: Tìm cấp số nhân Phương pháp giải bài tập dạng 5:
Bước 1: Xác định thành phần cấp số nhân như công bội q, số hạng nhập dãy Bước 2: Tìm công thức tổng quát cấp số nhân
Ví dụ 1:
Dãy số sau có phải là cấp số nhân không: 1; 0,2; 0,04; 0,008; 0,00016…
Đáp án:
Theo đề bài tao có U1 = 1, U2 = 0,2 => Công bội q = 0,2/1 = 0,2
Từ đó tao có U3 = 0,2 . 0,2 = 0,04
U4 = 0,04 . 0,2 = 0,008
U5 = 0,008 . 0,2 = 0,00016
Vậy dãy số 1; 0,2; 0,04; 0,008; 0,00016… là cấp số nhân có U1 = 1, công bội q = 0,2
Ví dụ 2:
Tìm cấp số nhân (Un) có 7 số hạng biết tổng của 5 số hạng đầu là 31, công bội q = 2
Đáp án:
Áp dụng công thức tính tổng các số hạng của cấp số nhân (Un) tao có:
S5 = U1 + U2 + U3 + U4 + U5
= U1 + U1.q + U2.q + U3.q + U4.q
= U1 + U1.q + U1.q.q + U1. q.q.q + U1.q.q.q.q.
= U1 + 2U1 + 4U1 + 8 U1 + 16U1
= 31U1
=> 31 = 31U1
=> U1 = 1
Vậy cấp spps nhân (U1) có 7 số hạng là: 1, 2, 4, 8, 16, 32, 64
Xem thêm: Hình avatar buồn, phụ nữ khóc đầy cảm xúc
Câu hỏi thường gặp 1. Ví dụ về sơ đồ suy nghĩ cấp số nhân? Lập sơ đồ suy nghĩ giúp người học phân tích, xâu chuỗi các kiến thức của 1 chủ đề một cách logic và khoa học. Từ đó giúp việc ghi nhớ và áp dụng kiến thức suôn sẻ rộng lớn. Có nhiều cách vẽ sơ đồ suy nghĩ công thức cấp số nhân. Dưới phía trên là 1 ví dụ mời các em học sinh cùng tham ô khảo.
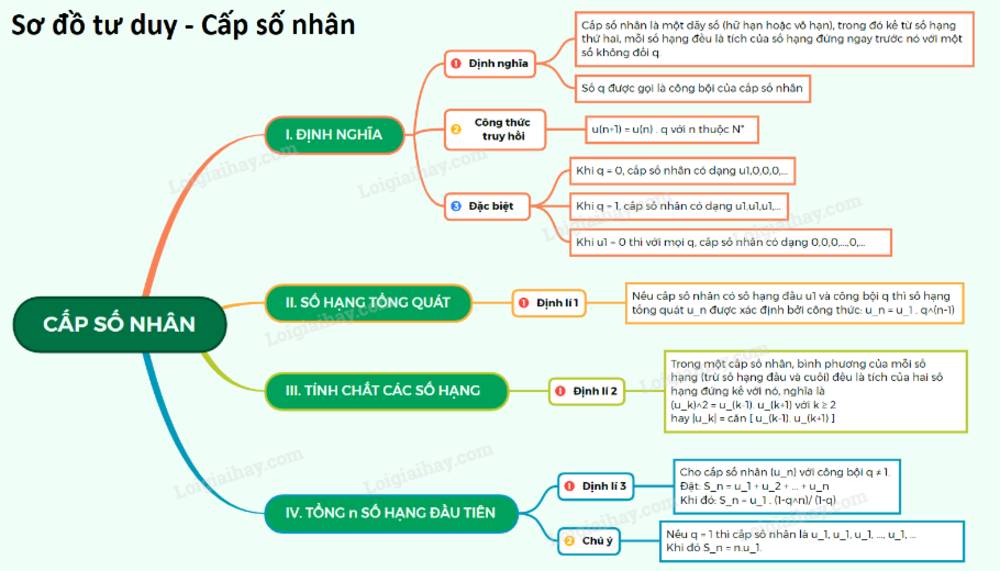
Sơ đồ suy nghĩ kiến thức cấp số nhân (sưu tầm Internet) 2. Cách ghi nhớ các công thức cấp số nhân thời gian nhanh chóng? Để ghi nhớ các công thức cấp số nhân thời gian nhanh chóng, hiệu quả học sinh cần chú ý:
Nắm vững các kiến thức về cấp số nhân như định nghĩa, tính chất, công thức… Tích cực luyện tập các dạng bài tập có tương quan để hiểu biết rõ và nhớ các công thức cấp số nhân. Mở rộng kiến thức, tăng cường sự sáng tạo bằng cách giải các bài tập nhập sách tham ô khảo và sách nâng lên. Tham khảo ý kiến thầy cô giáo với những nội dung còn thắc mắc hoặc ko hiểu biết, thảo luận với người mua hàng bè để mở rộng kiến thức, cách giải bài tập. Tham khảo vấn đề bên trên mạng internet từ các nguồn uy tín: các lớp dạy học toán online từ các giáo viên, các hội nhóm, diễn đàn về toán học.
Trên phía trên là toàn bộ kiến thức và một số dạng bài tập cơ bản về công thức cấp số nhân . The Dewey Schools trông mong với nội dung bài viết này các em học sinh có thể ghi nhớ và áp dụng vào giải bài tập công thức CSN một cách thành thạo. Mọi thắc mắc có tương quan vui vẻ lòng liên hệ với chúng tôi để được hỗ trợ nhập thời gian tham sớm nhất nhé.
