5 công thức tính diện tích hình tam giác vuông bạn cần biết

Công thức tính diện tích tam giác vuông là S = 1/2 x (a x b), trong đó a và b là độ dài hai cạnh góc vuông của tam giác vuông. Để tính diện tích, bạn nhân hai cạnh góc vuông lại với nhau, sau đó nhân kết quả với một nửa để lấy diện tích tam giác vuông. Ví dụ: Nếu độ dài hai cạnh góc vuông là 4cm và 5cm, ta tính S = 1/2 x (4 x 5) = 10cm².

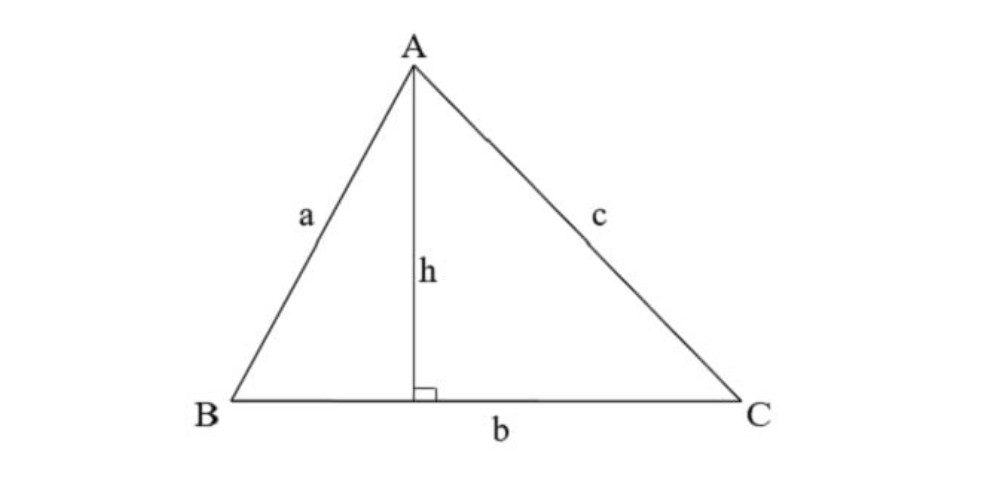
Công thức tính diện tích của tam giác vuông là: S = 1/2 x (cạnh góc vuông x cạnh góc vuông).
Để tính diện tích tam giác vuông, ta cần biết chiều dài của cạnh góc vuông.
Bước 1: Xác định chiều dài của cạnh góc vuông (a) trong tam giác vuông.
Bước 2: Áp dụng công thức tính diện tích tam giác vuông: S = 1/2 x (a x a).
Bước 3: Thực hiện phép tính để tính diện tích tam giác vuông.
Ví dụ: Nếu chiều dài cạnh góc vuông là 5 cm, thì diện tích tam giác vuông là: S = 1/2 x (5 x 5) = 1/2 x 25 = 12.5 cm^2.
Vậy, diện tích của tam giác vuông là 12.5 cm^2.

Công thức tính diện tích tam giác vuông dựa trên chiều dài và chiều rộng là: Diện tích tam giác vuông bằng một nửa tích của chiều dài và chiều rộng.
- Đầu tiên, xác định chiều dài và chiều rộng của tam giác vuông.
- Sau đó, áp dụng công thức tính diện tích tam giác vuông: S = 1/2 x (chiều dài x chiều rộng).
- Nhân tích của chiều dài và chiều rộng sau đó chia cho 2 để tìm diện tích tam giác vuông.
Ví dụ: Nếu chiều dài của tam giác vuông là 4 và chiều rộng là 3, ta áp dụng công thức: S = 1/2 x (4 x 3) = 6. Do đó, diện tích tam giác vuông là 6 đơn vị diện tích (đơn vị diện tích tùy thuộc vào đơn vị đo được sử dụng).

Công thức tính diện tích của tam giác vuông là S = 1/2 x (a x b), trong đó a và b lần lượt là độ dài của các cạnh góc vuông của tam giác. Để tính diện tích tam giác vuông, ta nhân tích của hai cạnh góc vuông sau đó chia cho 2. Ví dụ, nếu chiều dài cạnh góc vuông là 4 cm và chiều rộng cạnh góc vuông là 6 cm, ta có thể tính diện tích bằng cách thay vào công thức: S = 1/2 x (4 cm x 6 cm) = 12 cm².

Để tính diện tích của một tam giác vuông, bạn có thể sử dụng công thức sau: S = 1/2 x (đỉnh x cạnh đối diện).
- Đầu tiên, xác định đỉnh của tam giác vuông. Đỉnh này là góc vuông trong tam giác.
- Tiếp theo, xác định cạnh đối diện của đỉnh đó. Đây là cạnh nằm đối diện với góc vuông của tam giác.
- Áp dụng công thức, nhân độ dài đỉnh với độ dài cạnh đối diện và chia cho 2.
- Kết quả là diện tích của tam giác vuông.

Để tính diện tích của một tam giác vuông dựa trên chiều cao và cạnh đáy của nó, chúng ta có thể sử dụng công thức sau:
Diện tích (S) = 1/2 x cạnh đáy (a) x chiều cao (h)
Bước 1: Xác định cạnh đáy của tam giác vuông (a) và chiều cao của tam giác (h).
Bước 2: Áp dụng công thức diện tích tam giác vuông: S = 1/2 x a x h.
Bước 3: Thực hiện tính toán và tìm giá trị diện tích tam giác (S).

Để tính diện tích tam giác vuông, ta có thể áp dụng công thức sau đây:
S = 1/2 x (a x b)
Trong đó a và b lần lượt là hai cạnh góc vuông của tam giác vuông. Để áp dụng công thức này, làm theo các bước sau:
Bước 1: Xác định độ dài hai cạnh góc vuông của tam giác vuông. Đặt giá trị của a và b.
Bước 2: Sử dụng công thức tính diện tích tam giác vuông:
S = 1/2 x (a x b)
Bước 3: Thay vào giá trị của a và b từ bước 1 vào công thức ở bước 2.
Bước 4: Tính toán giá trị của S. Đây sẽ là diện tích của tam giác vuông.
Ví dụ: Giả sử ta có một tam giác vuông với hai cạnh góc vuông có độ dài lần lượt là a = 3 và b = 4. Ta áp dụng công thức trên:
S = 1/2 x (3 x 4) = 1/2 x 12 = 6
Vậy diện tích của tam giác vuông trong trường hợp này sẽ là 6.

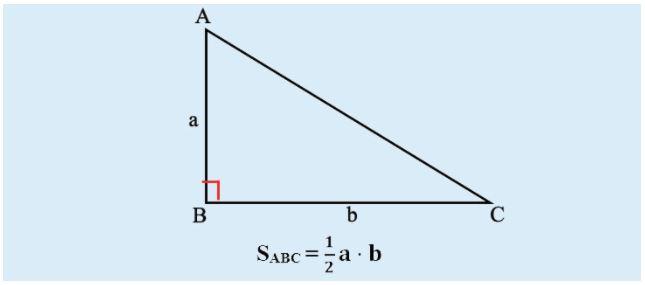
Công thức tính diện tích của tam giác vuông liên quan đến chiều cao từ đỉnh và cạnh đối diện. Để tính diện tích của tam giác vuông, ta có công thức S = 1/2 x (a x b). Trong đó, a và b là độ dài hai cạnh góc vuông của tam giác vuông. Tuy nhiên, công thức này cũng có thể được suy ra từ công thức tính diện tích tam giác chung của tam giác bất kỳ: S = (a x h)/2. Trong công thức này, h là chiều cao của tam giác tính từ đỉnh đến cạnh đối diện. Điều này có nghĩa là, để tính diện tích của tam giác vuông, ta có thể tính chiều cao từ đỉnh và cạnh đối diện rồi sử dụng công thức S = (a x h)/2.

Có cách tính diện tích tam giác vuông dựa trên diện tích và cạnh mà không cần biết chiều cao.
Công thức tính diện tích tam giác vuông là: S = 1/2 x (a x b), trong đó a và b lần lượt là độ dài hai cạnh góc vuông của tam giác vuông.
Bước 1: Xác định độ dài hai cạnh góc vuông của tam giác vuông.
Bước 2: Áp dụng công thức S = 1/2 x (a x b) để tính diện tích tam giác vuông.
Ví dụ: Nếu ta biết rằng cạnh góc vuông a có độ dài 4 và cạnh góc vuông b có độ dài 3, ta có thể tính diện tích tam giác vuông bằng cách áp dụng công thức S = 1/2 x (4 x 3) = 6.
Vậy, ta có thể tính diện tích tam giác vuông dựa trên diện tích và cạnh mà không cần biết chiều cao.

Chiều cao của tam giác vuông là đường thẳng vuông góc với đáy và đi qua đỉnh của tam giác. Để tìm chiều cao trong công thức tính diện tích tam giác vuông, chúng ta có thể sử dụng một trong hai cạnh góc vuông như là độ dài đáy.
1. Sử dụng cạnh góc vuông là đáy:
a) Lấy một đoạn thẳng (đáy) bằng một trong hai cạnh góc vuông của tam giác vuông.
b) Vẽ một đường vuông góc từ đỉnh đến đáy để tạo nên chiều cao, tạo thành một tam giác vuông.
c) Đo độ dài của chiều cao (h).
d) Sử dụng công thức tính diện tích tam giác vuông: S = 1/2 x (a x h) trong đó a là đáy, h là chiều cao.
2. Sử dụng cạnh góc vuông không phải là đáy:
a) Lấy một đoạn thẳng (không phải đáy) bằng một trong hai cạnh góc vuông của tam giác vuông.
b) Tạo một đoạn thẳng song song với đáy bằng cách vẽ đường vuông góc từ đỉnh đến đáy.
c) Đo độ dài của đoạn thẳng và gọi là chiều cao (h).
d) Sử dụng công thức tính diện tích tam giác vuông: S = 1/2 x (a x h) trong đó a là cạnh góc vuông không phải là đáy, h là chiều cao.
Chú ý rằng trong cả hai trường hợp, công thức tính diện tích tam giác vuông là S = 1/2 x (a x h), trong đó a là một cạnh góc vuông và h là chiều cao của tam giác.