Hình vỏ hộp chữ nhật là 1 trong hình không khí đem 6 mặt mày đều là hình chữ nhật với 8 đỉnh và 12 cạnh. Hai mặt mày của hình vỏ hộp tuy nhiên song cùng nhau được gọi là những mặt mày đối lập. Như vậy 6 mặt mày của hình vỏ hộp được chia thành 3 cặp mặt mày đối lập (trong cơ có một cặp mặt mày lòng và 2 cặp mặt mày bên).
Hai mặt mày đối lập nhau của hình vỏ hộp chữ nhật sẽ là nhị mặt mày lòng của hình vỏ hộp chữ nhật, những mặt mày sót lại đều là mặt mày mặt của hình vỏ hộp chữ nhật.
Bạn đang xem: Công thức tính diện tích hình hộp chữ nhật
Bài viết lách sau đây tiếp tục ra mắt cho tới chúng ta công thức tính diện tích S xung xung quanh, diện tích S toàn phần và độ cao của hình vỏ hộp chữ nhật nhằm hoàn toàn có thể vận dụng nhập cuộc sống thường ngày tương đương học hành.
Những công thức này đều được suy rời khỏi kể từ công thức tính diện tích S hình chữ nhật và chu vi hình chữ nhật nên khá dễ dàng ghi nhớ, chào chúng ta xem thêm.
Chúng tao đem hình vỏ hộp chữ nhật như sau:
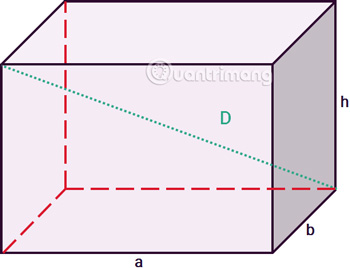
Công thức tính diện tích S hình vỏ hộp chữ nhật
Tính diện tích S xung xung quanh hình vỏ hộp chữ nhật
Diện tích xung xung quanh hình vỏ hộp chữ nhật vị chu vi lòng nhân với độ cao.
Diện tích toàn phần hình vỏ hộp chữ nhật
Diện tích toàn phần hình vỏ hộp chữ nhật vị tổng diện tích S của 6 mặt mày của hình vỏ hộp nằm trong lại.
Công thức tính diện tích S toàn phần hình vỏ hộp chữ nhật: vị tổng diện tích S xung xung quanh hình vỏ hộp chữ nhật và 2 đáy:
Trong đó:
Slà diện tích S hình vỏ hộp chữ nhật (xung xung quanh, toàn phần).alà chiều lâu năm hình vỏ hộp chữ nhật.blà chiều rộng lớn hình vỏ hộp chữ nhật.hlà độ cao hình vỏ hộp chữ nhật.
Công thức tính độ cao hình vỏ hộp chữ nhật
Từ công thức tính diện tích S xung xung quanh, diện tích S toàn phần của hình vỏ hộp chữ nhật tao hoàn toàn có thể suy ra sức thức tính độ cao của chính nó.
Chiều cao của hình vỏ hộp chữ nhật vị h = Sxq : P
- h là chiều cao
- p là chu vi mặt mày lòng. P.. = (a + b) x 2
Như vậy nhằm tính được độ cao hình vỏ hộp chữ nhật, những bạn phải ghi nhớ được công thức tính chu vi mặt mày lòng của chính nó.
Ví dụ:
Một hình vỏ hộp chữ nhật đem chiều lâu năm vị 40cm, chiều rộng lớn vị 25cm và diện tích S xung xung quanh là 5000cm2. Tính độ cao của hình vỏ hộp chữ nhật cơ vị bao nhiêu?
Giải:
Chu vi mặt mày lòng hình vỏ hộp chữ nhật là:
P = (a + b) x 2 = (40 + 25) x 2 = 90cm
Chiều cao của hình vỏ hộp chữ nhật là:
h = Sxq : P.. = 5000 : 90 = 55,5cm
Đáp số: 55,5cm
Ví dụ về tính chất diện tích S hình vỏ hộp chữ nhật
Bài 1: Cho hình vỏ hộp chữ nhật đem chiều lâu năm 20m, chiều rộng lớn 7m, độ cao 10m. Tính diện tích S xung xung quanh của hình vỏ hộp chữ nhật.
Xem thêm: Ảnh gái xinh che mặt
Giải:
Diện tích xung xung quanh của hình vỏ hộp chữ nhật là:
Sxq = 2h(a+b) = 2 x 10 x (20+7) = 540 m2.
Bài 2: Tính diện tích S toàn phần của một chiếc thùng hình chữ nhật đem độ cao là 3cm, chiều lâu năm là 5,4cm, chiều rộng lớn là 2cm.
Giải:
Diện tích xung xung quanh của thùng hình chữ nhật là:
Sxq = 2h(a + b) = 2 x 3 x (5,4 +2) = 44,4 cm2
Diện tích toàn phần của thùng hình chữ nhật là:
Stp = Sxq + 2.a.b = 44,4 + 2 x 5,4 x 2 = 66 cm2.
Bài 3: Diện tích xung xung quanh của một hình vỏ hộp chữ nhật là 420cm2 và đem độ cao là 7cm. Hãy tính chu vi lòng của hình vỏ hộp chữ nhật cơ.
Giải:
Vì diện tích S xung xung quanh của hình vỏ hộp chữ nhật vị chu vi lòng nhân với độ cao tao có:
Chu vi lòng của hình hình chữ nhật vị = Sxq : h = 420 : 7 = 60 (cm)
Bài 4: Một chống học tập hình vỏ hộp chữ nhật đem độ cao thấp như sau: lâu năm 7,8m, rộng lớn 6,2m, cao 4,3 m. Người tao cần thiết tô tường và trần nhà đất của căn chống này biết tổng diện tích S những cửa ngõ vị 8,1 mét vuông. Hãy tính diện tích S cần thiết quét tước tô của căn chống.
Giải: Diện tích xung xung quanh chống học tập (bao bao gồm cả diện tích S cửa) đó là diện tích S xung xung quanh của hình vỏ hộp chữ nhật.
Diện tích cần thiết quét tước tô của chống học tập tiếp tục vị diện tích S xung xung quanh trừ tổng diện tích S cửa ngõ cùng theo với diện tích S một lòng (trần nhà).
Diện tích xung xung quanh chống học tập là:
2 x 4,3 x (7,8 + 6,2) = 120,4 (m2)
Diện tích trần nhà đất của chống là:
7,8 x 6,2 = 48,36 (m2)
Diện tích cần thiết quét tước tô của chống học tập cơ là:
Xem thêm: Top hình nền Naruto 4k đẹp cho máy tính, laptop, điện thoại
(120,4 + 48,36) - 8,1 = 160,66 (m2)
Đáp số: 160,66 (m2)
Trên đó là tổ hợp những công thức về diện tích S xung xung quanh, diện tích S toàn phần của hình vỏ hộp chữ nhật và một trong những ví dụ rõ ràng. Còn vướng mắc gì thì các bạn hãy comment bên dưới nhằm nằm trong Quantrimang.com trao thay đổi nhé.