Công thức tính thể tích hình lập phương & hướng dẫn giải chi tiết

Hình lập phương là gì? Thể tích hình lập phương là gì?

Hình lập phương hoặc thường hay gọi là khối lập phương, là 1 trong khối nhiều diện đều với 3 chiều bao hàm 6 mặt mày là hình vuông vắn, 8 đỉnh, 12 cạnh đều nhau. Trong số đó, cứ 3 cạnh bắt gặp nhau sẽ tạo nên trở nên 1 đỉnh và bao gồm 4 đàng chéo cánh rời nhau bên trên 1 điều. Đồng thời, hình lập phương là tụ họp những điểm nằm cạnh vô và những điểm phía trên những đỉnh, cạnh và mặt mày này.

Bạn đang xem:

Ngoài đi ra, khối lập phương được xem là khối 6 mặt mày đều độc nhất, là 1 trong vô 5 khối nhiều diện đều với 9 mặt mày đối xứng. Hình lập phương cũng chính là hình khối lục diện vuông, rất có thể là hình vỏ hộp chữ nhật với những cạnh đều nhau hoặc hình khối mặt mày thoi vuông.

Còn thể tích khối lập phương chủ yếu là việc xác lập số đơn vị chức năng khối bị lắc trọn vẹn vày hình lập phương ê.

Tính hóa học của hình lập phương:

• Có 8 mặt mày phẳng lì đối xứng

• Có 12 cạnh đều nhau, 8 đỉnh, cứ 3 cạnh bắt gặp nhau bên trên một đỉnh

• Có 4 đàng chéo cánh cắt theo đường ngang bên trên 1 điều, là tâm đối xứng của hình lập phương.

• Đường chéo cánh những mặt mày mặt của khối lập phương đều lâu năm vày nhau

• Đường chéo cánh của hình lập phương cũng lâu năm đều nhau.

Công thức tính thể tích hình lập phương

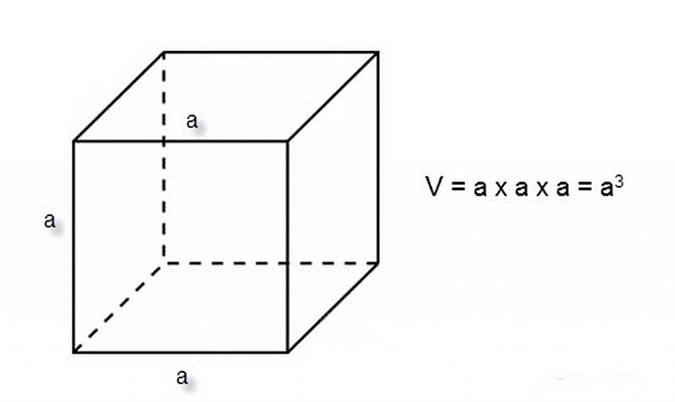
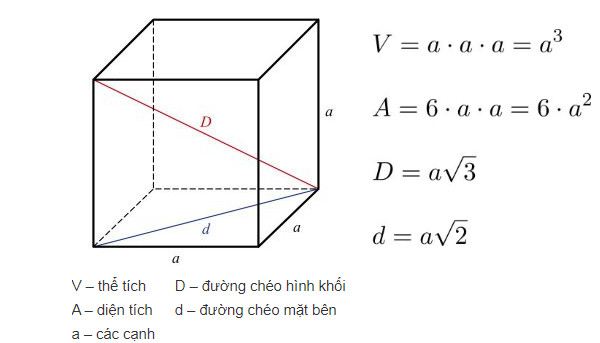
Thể tích hình lập phương được xem vày cạnh nhân với cạnh rồi nhân với cạnh.

Trong đó:

• V: thể tích của hình lập phương

• a: độ lâu năm cạnh của hình lập phương

• Đơn vị đo thể tích: m3 (mét khối)

Ví dụ:

Ví dụ 1: Ta với hình lập phương ABCDEFGH với cạnh a = 3 centimet. Tính thể tích hình lập phương ABCDEFGH.

Hướng dẫn giải:

Thể tích hình lập phương ABCDE là:

V(ABCDEFGH) = 3 x 3 x 3 = 27 cm3

Đáp số: 27cm3

Ví dụ 2: Cho một hình lập phương OPQRST với những cạnh đều đều nhau và vày 7cm . Hỏi thể tích hình lập phương OPQRST vày bao nhiêu?

Cách giải:

Theo đặc thù hình lập phương thì những cạnh đều đều nhau, nên ở hình OPQRST tớ với những cạnh đều nhau và vày độ quý hiếm a = 7cm.

Suy đi ra, V = a × a × a = 7 × 7 × 7 = 343 cm³

Đáp số: 343 cm3

Các dạng bài bác thói quen thể tích hình lập phương và cách thức giải

Với những nhỏ bé mới mẻ chính thức học tập kỹ năng và kiến thức thể tích hình lập phương tiếp tục bắt gặp một số trong những dạng bài bác tập dượt cơ phiên bản sau đây:

Dạng 1: Tính thể tích hình lập phương lúc biết chừng dài

Phương pháp giải: Dựa vô đề bài bác cho thấy thêm chừng lâu năm của những cạnh, ham muốn tính thể tích hình lập phương thì tớ lấy cạnh nhân với cạnh rồi nhân với cạnh.

Dạng 2: Tính thể tích khối lập phương lúc biết diện tích S xung xung quanh hoặc diện tích S toàn phần

Phương pháp giải: Thứ nhất, tất cả chúng ta rất cần phải tính diện tích S một mặt rồi mới mẻ tìm ra chừng lâu năm cạnh ứng. Sau Khi vẫn với được chừng lâu năm cạnh, tớ vận dụng phương pháp tính thể tích như dạng 1.

Dạng 3: Tính chừng lâu năm cạnh lúc biết thể tích

Phương pháp giải: Để dò la một số trong những a chưa chắc chắn tuy nhiên a x a x a = V thì thời điểm này chừng lâu năm cạnh của hình đó là a.

Dạng 4: So sánh thể tích của một hình lập phương với thể tích của một hình chữ nhật hoặc một hình lập phương khác

Phương pháp giải: kề dụng công thức nhằm tính thể tích từng hình rồi so sánh sánh

Dạng 5: Toán với điều văn

Phương pháp giải: Đọc kỹ đề bài bác, xác lập dạng Toán và đòi hỏi của đề bài bác rồi giải việc ê.

Bài thói quen thể tích hình lập phương vận dụng

Với kỹ năng và kiến thức tính thể tích hình lập phương những em sẽ tiến hành học tập vô công tác toán lớp 5. Dưới đó là một số trong những bài bác tập dượt ứng nhằm nhỏ bé rất có thể vận dụng kỹ năng và kiến thức vẫn học tập nhằm chinh phục:

Câu căn vặn trắc nghiệm

Câu 1. Hình nào là tại đây ko cần là hình nhiều diện?

A. hình lăng trụ

B. hình chóp

C. hình lập phương

D. hình vuông

Câu 2. Có thể phân tách một khối lập phương trở nên từng nào khối tứ diện rất có thể tích đều nhau tuy nhiên cá đỉnh của tứ diện cũng chính là đỉnh của hình lập phương?

Câu 3. Thể tích của khối lập phương cạnh 2a bằng

A. 8a^3

B. 2a^^3

C.a^3

D. 6a^3

Câu 4. Cho hình vỏ hộp đứng với một phía là hình vuông vắn cạnh a và với một phía với diện tích S là 3a^2. Thể tích khối vỏ hộp là?

A. a^3

B. 3a^3

C.2a^3

D. 4a^3

Câu 5. Hình lập phương có tính lâu năm hai tuyến phố chéo cánh vày 6 thì rất có thể tích là?

A. 2 √2

B.54 √2

C.24 √ 3

Xem thêm: Công thức làm sữa hạt bằng máy cực nhanh

D. 8

Câu 6. Số mặt mày của một khối lập phương là?

A. bốn

B. sáu

C. tám

D. mười

Câu 7. Số mặt mày phẳng lì đối xứng của hình lập phương la bao nhiêu?

A. sáu

B. bảy

C. tám

D. chín

Câu 8. Tính thể tích của khối lập phương hiểu được Khi rời chừng lâu năm cạnh xuống gấp đôi thì thể tích của chính nó rời 189 m3?

A. 216 m3

B. 8 m3

C. 27 m3

D. 64 m3

Câu 9. Khối lập phương là khối nhiều diện đều loại nào?

A. {5;3}

B. {3;4}

C. {4;3}

D.{3;5}

Câu 10. Khối lập phương rất có thể tích là 125 m3. Tính tổng diện tích S những mặt mày của hình lập phương đó?

A. 25 m2

B. 125 m2

C. 150 m2

D. 151 m2

Câu 11. Nếu tía độ dài rộng của một khối vỏ hộp chữ nhật tăng thêm k đợt thì thể tích khối vỏ hộp ứng là?

A. tăng k lần

B. tăng k^2 lần

C. tăng k^3 lần

D. tăng 3k^3 lần

Câu 12. Nếu tăng cường độ lâu năm cạnh của khối lập phương lên 4 đợt thì thể tích của chính nó tăng thêm từng nào lần?

A. 4

B. 16

C. 64

D. 8

Câu căn vặn tự động luận

Bài 1. Tổng diện tích S những mặt mày của một hình lập phương vày 150. Thể tích khối lập phương vày bao nhiêu?

Bài 2. Tổng diện tích S những mặt mày của một hình lập phương vày 96 cm2. Thể tích khối lập phương vày bao nhiêu?

Bài 3. Thể tích khối lập phương vày 27 thì tổng diện tích S những mặt mày của hình lập phương vày bao nhiêu?

Bài 4. Thể tích của khối lập phương ABCD.A'B'C'D' với đàng chéo cánh AC'  = a vày bao nhiêu?

Bài 5. Thể tích của khối lập phương ABCD.A'B'C'D' với đàng chéo cánh B'D = a √3 vày bao nhiêu?

Bài 6. Tính thể tích của khối lập phương ABCD.A'B'C'D' với đàng chéo cánh A'C = 6 cm?

Bài 7. Cho hình vỏ hộp đứng ABCD.A'B'C'D' với lòng là hình vuông vắn, cạnh mặt mày AA' = 3a và đàng chéo cánh AC' = 5a. Tính thể tích của khối vỏ hộp đứng trên?

Bài 8. Cho hình lập phương ABCD.A'B'C'D' với diện tích S tam giác ACD' vày √3a^2. Tính thể tích của hình lập phương vẫn mang lại.

Bài 9. Cho hình lập phương ABCD.A'B'C'D' với diện tích S tam giác B'AC vày 2 √3a^2. Tính thể tích của hình lập phương vẫn mang lại.

Bài 10. Khi chừng lâu năm cạnh hình lập phương gia tăng 2 centimet thì thể tích của chính nó gia tăng 98 cm3. Tính chừng lâu năm của cạnh lập phương thuở đầu.

Xem thêm: Tất cả những hình vô toán học tập cơ phiên bản cụ thể vừa đủ nhất

Kinh nghiệm đoạt được toán lớp tính V hình lập phương

Để canh ty nâng lên hiệu suất cao học tập toán hình phát biểu cộng đồng, kỹ năng và kiến thức tính thể tích của khối lập phương phát biểu riêng rẽ thì những em rất có thể xem thêm thêm thắt một số trong những tay nghề sau:

Tạo sự hào hứng khi tham gia học toán hình mang lại nhỏ bé với Monkey Math

Toán học tập là cỗ môn khá ráo mát, nhất là toán hình. Vậy nên, nhằm tạo ra sự hào hứng mang lại nhỏ bé vô quy trình học tập, ba mẹ rất có thể xem thêm thêm thắt khí cụ dạy dỗ toán tận nhà Monkey Math. Đây là ứng dụng học tập toán kể từ duy online dành riêng cho trẻ nhỏ thiếu nhi và tè học, với nội dung được thiết kế bám sát công tác GDPT tiên tiến nhất của Sở, nhằm đáp ứng chuẩn bị vừa đủ nền tảng kỹ năng và kiến thức nhằm nhỏ bé phần mềm vô thực tiễn biệt hao hao tương hỗ việc học tập bên trên ngôi trường lớp chất lượng tốt rộng lớn.

Ở phía trên, Monkey Math tiếp tục áp dụng nhiều cách thức dạy dỗ học tập không giống nhau kể từ cách thức tiếp thu kiến thức tích vô cùng, học tập trải qua trò nghịch ngợm, học tập qua quýt sách bài bác tập dượt hỗ trợ. Cùng với nội dung bám sát nhiều chủ thể, bao hàm những kỹ năng và kiến thức về hình học tập được cá thể hoá mang lại từng đối tượng người dùng, phân tạo thành nhiều Lever nhằm phù phù hợp với năng lượng của trẻ con.

Ngoài đi ra, Monkey Math còn xây dựng nội dung với hình hình ảnh hoạt hoạ ngộ nghĩnh, tiếng động sinh sống động canh ty tăng kỹ năng thu nhận, ghi ghi nhớ của nhỏ bé chất lượng tốt rộng lớn. Cùng với khá nhiều sinh hoạt được chèn ghép chuyên nghiệp canh ty tạo ra niềm yêu thích khi tham gia học toán rộng lớn đối với học tập bên trên giấy tờ thường thì.

Vậy nên, nhằm làm rõ rộng lớn về phần mềm học tập toán này, ba mẹ rất có thể xem thêm qua quýt Clip sau hoặc ĐK sẽ được tư vấn tốt nhất có thể nhé.

Nắm vững vàng kỹ năng và kiến thức cơ phiên bản về hình lập phương

Để giải được bài bác thói quen thể tích của khối lập phương, yên cầu những em cần nắm vững vàng những kỹ năng và kiến thức nền tảng cơ phiên bản của mô hình học tập này kể từ đặc thù, định nghĩa và những công thức tương quan. Với phần này, yên cầu ba mẹ cần chỉ dẫn, phân tích và lý giải rõ ràng nhằm nhỏ bé hiểu hao hao ghi ghi nhớ. Đồng thời nên thông thường xuyên soát lại kỹ năng và kiến thức nhằm coi nhỏ bé với quên thường bị sai nghiêng vấn đề hay là không, nhằm thông qua đó được bố trí theo hướng xử lý và gia tăng đúng lúc.

Xem thêm: Ảnh gái xinh che mặt

Luyện tập dượt thông thường xuyên là nhân tố bắt buộc

Dù con cái vẫn nắm vững kỹ năng và kiến thức rồi tuy nhiên còn nếu như không được rèn luyện, thực hành thực tế thông thường xuyên chắc hẳn rằng tiếp tục vô cùng nhanh chóng quên. Vậy nên, ba mẹ nên đòi hỏi, khuyến khích trẻ con thực hiện bài bác tập dượt hao hao thực hành thực tế nhập cuộc những cuộc ganh đua, tổ chức triển khai những trò nghịch ngợm về toán học…. Chính việc được tập luyện thông thường xuyên tiếp tục kích ứng óc cỗ của nhỏ bé học tập, trí tuệ, ghi ghi nhớ và áp dụng một cơ hội chất lượng tốt rộng lớn.

Kết luận

Trên đó là những vấn đề về kỹ năng và kiến thức cơ phiên bản cách tính thể tích hình lập phương. Đây là kỹ năng và kiến thức không chỉ có vận dụng vô toán học tập tuy nhiên trong thực tiễn biệt phần mềm thật nhiều, nên ba mẹ hãy xem thêm để sở hữu thêm thắt vấn đề chỉ dẫn nhỏ bé học tập chất lượng tốt rộng lớn. Đồng thời, nếu như không tồn tại nhiều thời hạn và tay nghề trong các việc dạy dỗ nhỏ bé học tập toán thì rất có thể xem thêm phần mềm Monkey Math nhé.