beyeu
beyeu
Trang chủ Giáo Dục Cách tính bán kính đường tròn ngoại tiếp tam giác

Cách tính bán kính đường tròn ngoại tiếp tam giác

Cách tính nửa đường kính đàng tròn xoe nước ngoài tiếp tam giác dưới đấy là một trong mỗi công thức cần thiết những em lớp 12 cần thiết ghi ghi nhớ nhằm áp dụng đo lường và tính toán sớm nhất những việc tương quan cho tới đàng tròn xoe nước ngoài tiếp tam giác và tạo ra thành quả đúng chuẩn.

Trong kì thi đua trung học phổ thông Quốc gia môn Toán thì con số công thức cần thiết ghi hãy nhờ rằng không nhỏ. Đối với những bài bác thi đua trắc nghiệm, điều quan trọng là những em học viên cần thiết cầm kỹ năng và kiến thức rộng lớn và với cách thức giải nhanh chóng hiệu suất cao nhằm rất có thể ghi điểm tối đa. Vậy bên dưới đấy là toàn cỗ công thức nửa đường kính đàng tròn xoe nước ngoài tiếp tam giác mời mọc chúng ta nằm trong đón gọi. Hình như chúng ta coi tăng cỗ đề ôn thi đua trung học phổ thông Quốc gia môn Toán, phân dạng thắc mắc và bài bác luyện nhập đề thi đua trung học phổ thông Quốc gia môn Toán.

Bạn đang xem: Cách tính bán kính đường tròn ngoại tiếp tam giác

1. Công thức tính nửa đường kính đàng tròn xoe nước ngoài tiếp

Cho tam giác ABC với AB = c, AC = b, BC = a, R là nửa đường kính đàng tròn xoe nước ngoài tiếp tam giác ABC, S là diện tích S tam giác ABC

Cách 1: Sử dụng công thức diện tích S tam giác

S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}}

Cách 2: Sử dụng lăm le lí Sin nhập tam giác

Ta có:

\begin{matrix} \dfrac{a}{{\sin \widehat A}} = \dfrac{b}{{\sin \widehat B}} = \dfrac{c}{{\sin \widehat C}} = 2R \hfill \\ \Rightarrow R = \dfrac{a}{{2\sin \widehat A}} = \dfrac{b}{{2\sin \widehat B}} = \dfrac{c}{{2\sin \widehat C}} \hfill \\ \end{matrix}

Cách 3: Tính hóa học của tam giác vuông

- Tâm đàng tròn xoe nước ngoài tiếp tam giác vuông là trung điểm của cạnh huyền, bởi vậy nửa đường kính đàng tròn xoe nước ngoài tiếp tam giác vuông chủ yếu bởi vì nửa phỏng nhiều năm cạnh huyền.

Cách 4: Sử dụng hệ tọa độ

- Tìm tọa phỏng tâm O của đàng tròn xoe nước ngoài tiếp tam giác ABC

- Tìm tọa phỏng một trong những tía đỉnh A, B, C (nếu ko có)

- Tính khoảng cách kể từ tâm O cho tới một trong những tía đỉnh A, B, C, phía trên đó là nửa đường kính cần thiết tìm: R = OA = OB = OC

*Cách tính nửa đường kính đàng tròn xoe nước ngoài tiếp tam giác đều

Một tam giác đều là tam giác đối với tất cả tía cạnh và tía góc đều bằng nhau. Bán kính đàng tròn xoe nước ngoài tiếp của tam giác đều chủ yếu bởi vì phỏng nhiều năm một cạnh của tam giác bại.

Do tam giác đều sở hữu những cạnh đều bằng nhau, tao rất có thể dùng công thức sau nhằm tính nửa đường kính đàng tròn xoe nước ngoài tiếp của tam giác đều:

r=\frac{a}{2}

Trong đó:

  • r là nửa đường kính đàng tròn xoe nước ngoài tiếp của tam giác đều.
  • a là phỏng nhiều năm một cạnh của tam giác đều.

Chú ý rằng công thức này chỉ vận dụng được cho những tam giác đều. Nếu tam giác ko nên tam giác đều, bạn phải dùng công thức tính bán kính đường tròn ngoại tiếp của tam giác như đang được trình diễn nhập câu vấn đáp trước bại.

2. Ví dụ tính nửa đường kính đàng tròn xoe nước ngoài tiếp tam giác

Ví dụ 1: Cho hình thang vuông ABCD với \widehat A = \widehat B = {90^0} , BC = 2AD = 2a. Gọi H là hình chiếu vuông góc của B lên AC, M là trung điểm của HC. Tìm tâm và nửa đường kính của đàng tròn xoe nước ngoài tiếp tam giác BDM.

Gợi ý trả lời

Vẽ hình:

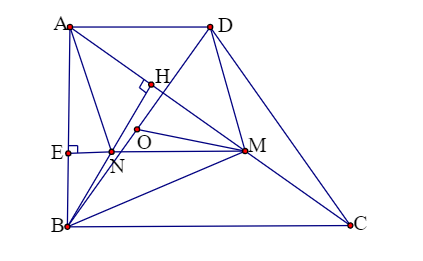
Gọi N là trung điểm của BH thì MN là đàng khoảng của tam giác HBC => MN ⊥ AB

Xem thêm: Công thức làm sữa hạt bằng máy cực nhanh

Mặt không giống BH ⊥ AM

=> N là trực tâm của tam giác ABM

=> AN ⊥ BM

Do MN// = \frac{1}{2}BC => MN //= AD

Nên ADMN là hình bình hành => AN // DM

Từ bại tao có: DM ⊥ MB hoặc tam giác DBM vuông bên trên M nên tâm đàng tròn xoe nước ngoài tiếp tam giác DBM là trung điểm O của BD

Ta có: R = MO = \frac{1}{2}BD = \frac{1}{2}\sqrt {A{B^2} + A{D^2}} = \frac{1}{2}\sqrt {4{a^2} + {a^2}} = \frac{{a\sqrt 5 }}{2}

Ví dụ 2:  Cho tam giác ABC với AB = 3, AC = 5 và BC = 6. Tính nửa đường kính đàng tròn xoe nước ngoài tiếp tam giác ABC.

Gợi ý đáp án

Theo công thức Hê - rông, diện tích S tam giác A B C là:

\begin{aligned} &S=\frac{\sqrt{(A B+A C+B C)(A B+B C-A C)(A B+A C-B C)(B C+A C-A B)}}{4} \\ &=\frac{\sqrt{(3+5+6)(3+6-5)(3+5-6)(6+5-3)}}{4} \\ &=\frac{\sqrt{14.4 .2 .8}}{4}=\frac{\sqrt{896}}{4}=\frac{8 \sqrt{14}}{4}=2 \sqrt{14} \end{aligned}

Bán kính đàng tròn xoe nước ngoài tiếp tam giác ABC là:

\mathrm{R}=\frac{\mathrm{AB} \cdot \mathrm{AC} \cdot \mathrm{BC}}{4 \mathrm{~S}}=\frac{3 \cdot 5 \cdot 6}{4 \cdot 2 \sqrt{14}}=\frac{90}{8 \sqrt{14}}=\frac{45}{4 \sqrt{14}} .

3. Bài thói quen nửa đường kính đàng tròn xoe nước ngoài tiếp tam giác

Bài 1: Cho tam giác ABC vuông bên trên A với AB = 1; AC = 4. Gọi M là trung điểm AC.

a) Tính diện tích S tam giác ABC.

b) Tính bán kính R1 của đàng tròn xoe nước ngoài tiếp tam giác ABC.

c) Tính bán kính R2 của đàng tròn xoe nước ngoài tiếp tam giác CBM.

Bài 2: Cho tam giác ABC với BC = 10. Gọi (I) là đàng tròn xoe với tâm I nằm trong cạnh BC và xúc tiếp với những cạnh AB, AC thứu tự bên trên M và N. thạo đàng tròn xoe (I) với nửa đường kính bởi vì 3 và 2IB = 3IC. Tính nửa đường kính R của đàng tròn xoe nước ngoài tiếp tam giác ABC.

Bài 3: Cho tam giác ABC vuông bên trên A, Ab = 5cm, AC = 12cm. Tính nửa đường kính đàng tròn xoe nước ngoài tiếp tam giác ABC.

Bài 4: Cho hình chữ nhật ABCD với AB = 12cm, BC = 5cm. Chứng minh rằng 4 điểm A, B, C, D nằm trong phía trên một đàng tròn xoe. Tính nửa đường kính đàng tròn xoe bại.

Bài 5: Cho hình vuông vắn ACBD. Gọi M, N thứu tự là trung điểm của AB và BC. Gọi E là phú điểm của AM và DN

a) Tính số đo góc CEN

Xem thêm: Chu vi xích đạo của trái đất

b) Chứng minh 4 điểm A, D, E, M nằm trong tuỳ thuộc 1 đàng tròn xoe.

c) Xác lăm le tâm đàng tròn xoe nước ngoài tiếp trải qua tía điểm B, D, E,.

Bài 6; Cho tam giác ABC với AB = 3, AC = 5 và BC = 6. Tính nửa đường kính đàng tròn xoe nước ngoài tiếp tam giác ABC.

BÀI VIẾT NỔI BẬT