Diện tích hình tam giác - Công thức tính diện tích hình tam giác

Hình tam giác là một trong những hình cực kỳ không xa lạ của cục môn toán học tập. Mỗi mô hình tam giác lại sở hữu công thức tính không giống nhau. Hãy nằm trong LabVIETCHEM đón hiểu nội dung bài viết sau nhằm dò xét hiểu cụ thể về phong thái tính diện tích hình tam giác và giải một trong những bài bác tập dượt vận dụng tiếp sau đây nhé.

Hình tam giác hoặc tam giác là một trong những trong mỗi mô hình cơ phiên bản của hình học: hình hai phía phẳng phiu sở hữu phụ vương đỉnh là phụ vương điểm ko trực tiếp mặt hàng với phụ vương cạnh là phụ vương đoạn trực tiếp nối những đỉnh cùng nhau. Hình tam giác là một trong những nhiều giác sở hữu số cạnh tối thiểu (chỉ sở hữu phụ vương cạnh).

Bạn đang xem: Diện tích hình tam giác - Công thức tính diện tích hình tam giác

Hình tam giác là gì?

Có từng nào loại tam giác

Tam giác rất có thể tạo thành 7 loại tam giác như:

1. Tam giác thường

Đây là loại tam giác cơ phiên bản nhất với phỏng lâu năm những cạnh không giống nhau và số đo góc nhập cũng rất khác nhau. Tam giác thông thường cũng rất có thể bao gồm những tình huống đặc biệt quan trọng của tam giác.

2. Tam giác cân

Là loại tam giác sở hữu nhì cạnh đều bằng nhau, nhì cạnh này được gọi là nhì cạnh mặt mũi. Đỉnh của tam giác cân nặng đó là kí thác điểm của nhì cạnh mặt mũi. Góc tạo ra bởi vì đỉnh được gọi là góc ở đỉnh, những góc sót lại gọi là gọi là góc ở lòng và nhì góc lòng thì đều bằng nhau.

3. Tam giác đều

Tam giác này là tình huống đặc biệt quan trọng của tam giác cân nặng với phụ vương cạnh đều bằng nhau. Nó sở hữu đặc điểm là sở hữu phụ vương góc đều bằng nhau và bởi vì 60^o

4. Tam giác vuông

Là loại tam giác sở hữu một góc bởi vì 90^o (hay hay còn gọi là góc vuông).

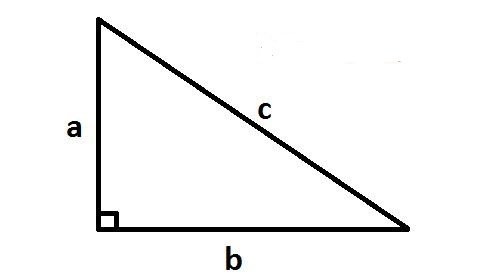
Tam giác vuông sở hữu một góc 90^o

5. Tam giác tù

Tam giác tù là tam giác sở hữu một góc nhập to hơn 90^o (gọi là góc tù) hay như là một góc ngoài bé nhiều hơn 90^o (gọi là nhọn).

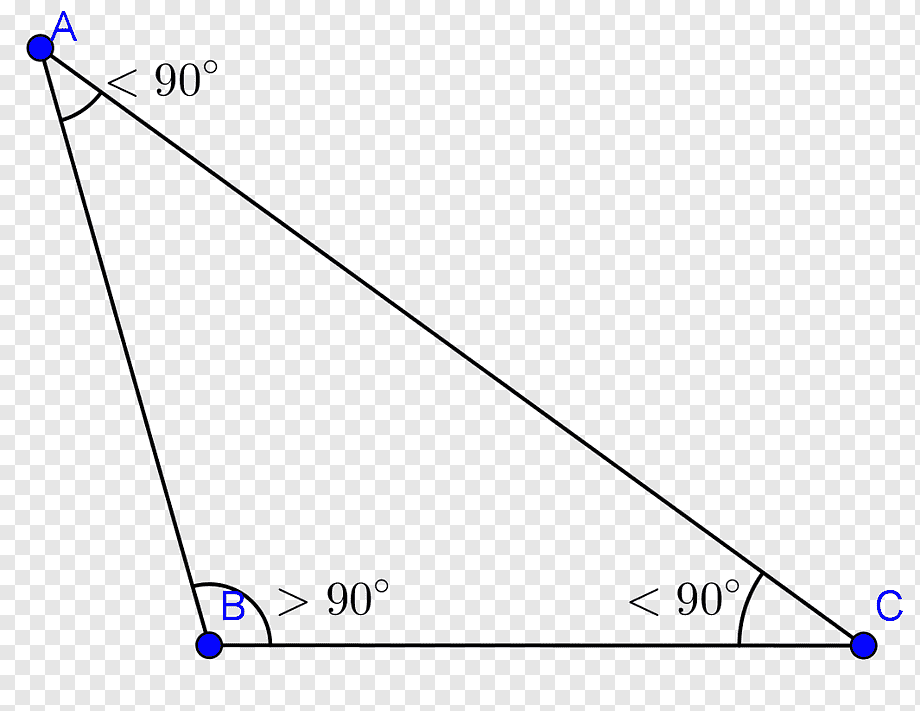
Tam giác tù

6. Tam giác nhọn

Là loại tam giác bao gồm phụ vương góc nhập đều nhỏ rộng lớn 90^o (ba góc nhọn) hoặc bao gồm toàn bộ những góc ngoài to hơn 90^o (sáu góc tù).

7. Tam giác vuông cân

Đây là loại tam giác vừa phải là tam giác vuông, vừa phải là tam giác cân nặng.

Công thức tính diện tích S hình tam giác

1. Cách tính diện tích S tam giác thường

Diện tích của tam giác thông thường được xem bằng phương pháp nhân độ cao với phỏng lâu năm của lòng, tiếp sau đó lấy thành quả phân tách mang đến nhì. cũng có thể hiểu một cơ hội khác: diện tích S tam giác thông thường tiếp tục bởi vì ½ tích của độ cao với chiều lâu năm cạnh lòng của tam giác.

Đơn vị tính: cm², dm², m²,…

Công thức tính diện tích S tam giác thường

S = (a x h)/2

Trong đó:

• a là chiều lâu năm lòng tam giác (đáy là một trong những nhập phụ vương cạnh của tam giác tùy nằm trong nhập cơ hội bịa của những người tính)
• h là độ cao của tam giác, ứng với phần lòng chiếu lên (chiều cao của một tam giác được xác lập là đoạn trực tiếp hạ kể từ đỉnh xuống lòng, mặt khác vuông góc với lòng của tam giác).

Công thức suy ra:

h = (S x 2) / a hoặc a = (S x 2) / h

2. Công thức tính diện tích tam giác vuông

Diện tích tam giác vuông được xem bằng: ½ tích độ cao với chiều lâu năm lòng hoặc bởi vì một nửa chiều lâu năm 2 cạnh góc vuông. 

Công thức tính diện tích S hình tam giác vuông

S = ½ (a x b)

Trong đó: a, b là phỏng lâu năm của nhì cạnh góc vuông

3. Công thức tính diện tích S tam giác cân

Diện tích của tam giác thăng bằng tích của độ cao nối kể từ đỉnh tam giác ê cho tới cạnh lòng tam giác và chiều lâu năm lòng tam giác cân nặng, tiếp sau đó lấy thành quả phân tách mang đến 2.

Công thức tính

S = ½ (a x h)

Trong đó:

• a là phỏng lâu năm của cạnh đáy
• b là phỏng lâu năm của nhì cạnh bên
• h là lối cao kể từ đỉnh xuống cạnh lòng (theo hình vẽ)

4. Tính diện tích S tam giác đều

Công thức tính diện tích S hình tam giác đều (áp dụng toan lý Heron)

S = a² x (√3/4)

Xem thêm: Hình Nền OPPO ❤️ Tuyển Tập Ảnh Nền Điện Thoại OPPO - Gấu Đây - Takimart

Trong đó: a là phỏng lâu năm những cạnh

5. Tính diện tích tam giác vuông cân

Công thức tính:

S_ABC = ½ x (a²)

Trong đó: tam giác ABC vuông cân nặng bên trên A và a là phỏng lâu năm nhì cạnh góc vuông.

Một số bài bác tập dượt vận dụng tính diện tích S hình tam giác

Bài tập dượt 1: Tính diện tích S của hình tam giác thông thường biết:

1. Độ lâu năm của lòng là 15 m, độ cao 12 m.

2. Độ lâu năm lòng 6 centimet và chều cao 4,5 centimet.

Lời giải:

1. gí dụng công thức tính diện tích S của tam giác thông thường tớ sở hữu diện tích S của hình tam giác là: 

(15 x 12) : 2 = 90 (m²)

2. Diện tích cua hình tam giác là:

(6 x 4,5) : 2 = 13,5 (cm²)

Bài tập dượt 2: Tính diện tích S của tam giác vuông với

1. Hai cạnh của góc vuông theo thứ tự là 3 centimet và 4 centimet.

2. Hai cạnh của góc vuông theo thứ tự là 6 centimet và 8 centimet.

Lời giải:

1. Diện tích của tam giác là:

(3 x 4) : 2 = 6 (cm²)

2. Diện tích của tam giác là:

(6 x 8) : 2 = 24 (cm²)

Bài tập dượt 3: Hãy tính diện tích S của tam giác cân nặng có

1. Độ lâu năm của cạnh lòng bởi vì 6 centimet và lối cao là 7 centimet.

2. Độ lâu năm của cạnh lòng bởi vì 5 m và lối cao là 3,2 m.

Lời giải:

1. Diện tích của tam giác bằng:

(6 x 7) : 2 = 21 (cm²)

2. Diện tích của tam giác là:

(5 x 3,2) : 2 = 8 (m²)

Bài tập dượt 4: Tính diện tích S của tam giác đều khi:

1. Độ lâu năm của một cạnh tam giác bởi vì 6 centimet và lối cao là 10 cm

2. Độ lâu năm của một cạnh tam giác là 4 centimet và lối cao bởi vì 5 cm

Lời giải:

1. Diện tích tam giác là: 

(6 x 10) : 2= 30 (cm²)

2. Diện tích tam giác là:

Xem thêm: Trần Đức Phú BDS - Chuyên Gia Bất Động Sản Tại Công Ty Địa Ốc Phú Long

(4 x 5) : 2 = 10 (cm²)

Trên đấy là một trong những công thức cơ phiên bản về tính chất diện tích hình tam giác nhưng mà LabVIETCHEM vẫn tổ hợp, kỳ vọng qua chuyện nội dung bài viết vẫn rất có thể giúp cho bạn hiểu rất có thể vận dụng nhằm dò xét rời khỏi được diện tích S của những mô hình tam giác một cơ hội đơn giản. Nếu còn gì vướng mắc hoặc bài bác tập dượt tương quan cần thiết trả lời, nài sướng lòng nhằm lại comment tức thì bên dưới nội dung bài viết hoặc gọi cho tới số đường dây nóng hoặc nhắn tin yêu mang đến trang web beyeu.edu.vn sẽ được trả lời sớm nhất có thể.

Xem thêm: 

• Phân biệt lối tròn xoe và hình tròn? Cách tính 2 lần bán kính hình tròn