Vectơ trong không gian
A. CÁC KIÊN THỨC CẦN NHỚ
I. CÁC ĐỊNH NGHĨA
1. Vectơ, giá và độ dài của vectơ
- Vectơ trong không gian là một đoạn thẳng có hướng.
Kí hiệu chỉ vectơ có điểm đầu A, điểm cuối B. Vectơ còn được kí hiệu là
….
2. Hai vectơ bằng nhau, vectơ – không
II. PHÉP CỘNG VÀ PHÉP TRỪ VECTƠ
1. Định nghĩa
2. Tính chất
3. Các quy tắc cần nhớ khi tính toán
a) Quy tắc ba điểm
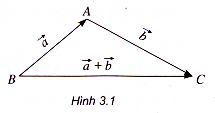
Với ba điểm A, B, C bất kì ta có :
+
=
=
–
=
+ (-
) =
+
=
+
(h.3.1).
b) Quy tắc hình bình hành
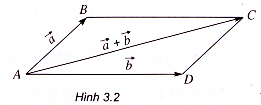
Với hình bình hành ABCD ta có :
=
+
(h.3.2).
c) Quy tắc hình hộp
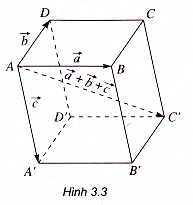
Cho hình hộp ABCD.A’B’C’D’ với AB, AD, AA’ là ba cạnh có chung đỉnh A và AC’ là đường chéo (h.3.3), ta có :
=
+
+
.
d) Mở rộng quy tắc ba điểm
Cho n điểm bất kì (h.3.4),
ta có: +
+ …
=
III. TÍCH CỦA VECTƠ VỚI MỘT SỐ
1. Định nghĩa. Cho số k ≠ 0 và vectơ ≠
. Tích của vectơ ã với số k là một vectơ, kí hiệu là k
, cùng hướng với
nếu k > 0, ngược hướng với
nếu k < 0 và có độ dài bằng |k|.|
|.
2. Tính chất. Với mọi vectơ ,
và mọi số m, n ta có :
IV. ĐIỂU KIỆN ĐỔNG PHẲNG CỦA BA VECTƠ
1. Khái niệm về sợ đồng phẳng của ba vecto trong không gian
Cho ba vectơ ,
,
đều khác
trong không gian. Từ một điểm o bất kì ta vẽ
=
,
=
,
=
. Khi đó xảy ra hai trường hợp :Khái niệm về sự đồng phẳng của ba vectơ trong không gian
2. Định nghĩa
Trong không gian, ba vectơ được gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.
3. Điều kiện để ba vectơ đồng phẳng
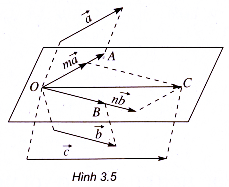
Định lí 1. Trong không gian cho hai vectơ không cùng phương và
và một vectơ
. Khi đó ba vectơ
,
,
đồng phẳng khi và chỉ khi có cặp số m, n sao cho
= m
+ n
. Ngoài ra cặp số m, n là duy nhất (h.3.5).
4. Phân tích (biểu thị) một vectơ theo ba vectơ không đồng phẳng
Định lí 2
Cho ,
,
là ba vectơ không đồng phẳng. Với mọi vectơ
trong không gian ta đều tìm được một bộ ba số m, n, p sao cho
= m
+ n
+ p
. Ngoài ra bộ ba số m, n, p là duy nhất.
Cụ thể =
,
=
,
=
,
=
(h.3.6)
và =
+
+
với
= m
,
= n
,
= p
.
Khi đó : = m
+ n
+ p
.
B. DẠNG TOÁN CƠ BẢN
Vấn đề 1
Xác định các yếu tố của vectơ
1. Phương pháp giải
a) Dựa vào định nghĩa các yếu tố của vectơ;
b) Dựa vào các tính chất hình học của hình đã cho.
2. Ví dụ
Ví dụ 1. Cho hình lăng trụ tam giác ABC.A’B’C’. Hãy nêu tên các vectơ bằng nhau có điểm đầu và điểm cuối là các đỉnh của lăng trụ.
Giải
Theo tính chất của hình lăng trụ ta suy ra :
=
,
=
,
=
= –
,
= –
,
= –
=
=
= –
= –
= –
= –
,
= –
,
= –
Ví dụ 2. Cho hình hộp ABCD.A’B’C’D’. Hãy kể tên các vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp lần lượt bằng các vectơ ,
và
.
Giải
Theo tính chất của hình hộp (h.3.8) ta có : =
=
=
=
=
=
=
Ta cũng có :
= –
= –
= -$latex \overrightarrow{C’D’} $
= –
= –
=
= –
, v.v…
Vấn đề 2
Chứng minh cốc đẳng thức về vectơ
1. Phương pháp giải
a) Sử dụng quy tắc ba điểm, quy tắc hình bình hành, quy tắc hình hộp để biến đổi vế này thành vế kia và ngược lại.
b) Sử dụng các tính chất của các phép toán về vectơ và các tính chất hình học của hình đã cho.
2. Ví dụ
Vi dụ 1. Cho hình hộp ABCD.EFGH. Chứng minh rằng +
+
=
.
Giải
Theo tính chất của hình hộp :
+
+
=
+
+
=
.
Dựa vào quy tắc hình hộp ta có thể viết ngay kết quả :
+
+
=
(h.3.9).
Ví dụ 2. Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Chứng minh rằng
+
=
+
Giải
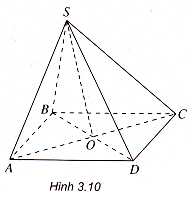
Gọi O là tâm của hình bình hành ABCD (h.3.10).
Ta có :
+
= 2
(1)
và +
= 2
(2)
So sánh (1) và (2) ta suy ra +
=
+
.
Ví dụ 3. Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD. Chứng minh rằng
+
=
+
.
Giải
Gọi O là tâm hình chữ nhật ABCD (h.3.11).
Ta có: || = |
| = |
| = |
| .
=
=
+
+2.
.
=
=
+
+ 2
.
⇒ +
= 2
+
+
+ 2
(
+
).
Mà +
=
nên
+
= 2
+
+
Tương tự ta có : +
= 2
+
+
.
Từ đó ta suy ra: +
=
+
.
Ví dụ 4. Cho đoạn thẳng AB. Trên đoạn thẳng AB ta lấy điểm C sao cho
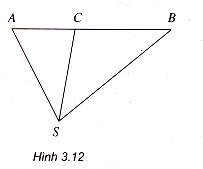

Giải
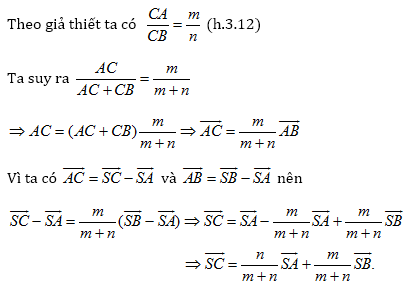
Vấn đề 3
Chứng minh ba vectơ ,
,
đồng phẳng
1. Phương pháp giải
a) Dựa vào định nghĩa : Chứng tỏ các vectơ ,
,
có giá song song với một mặt phẳng.
b) Ba vectơ ,
,
đồng phẳng ⇔ có cặp số m, n duy nhất sao cho
= m
+ n
, trong đó
và
là hai vectơ không cùng phương.
2. Ví dụ
Ví dụ 1. Cho tứ diện ABCD. Trên cạnh AD lấy điểm M sao cho = 3
và trên cạnh BC lấy điểm N sao cho
= – 3
. Chứng minh rằng ba vectơ
,
,
đồng phẳng.
Giải
Theo giả thiết = – 3
và = – 3
(h.3.13).
Mặt khác =
+
+
(1)
và =
+
+
⇒ 3 = 3
+ 3
+ 3
(2)
Cộng đẳng thức (1) và (2) với nhau vế theo vế, ta có
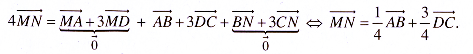
Hệ thức trên chứng tỏ rằng ba vectơ ,
,
đồng phẳng.
Ví dụ 2. Cho hình hộp ABCD.EFGH. Gọi I là giao điểm hai đường chéo của hình bình hành ABFE và K là giao điểm hai. đường chéo của hình bình hành BCGF. Chứng minh rằng ba vectơ ,
,
đồng phẳng.
Giải
Vectơ có giá thuộc mặt phẳng (ABCD). Vectơ
có giá song song với đường thẳng AC thuộc mặt phẳng (ABCD).
Vectơ có giá song song với đường thẳng BC thuộc mặt phẳng (ABCD). Vậy ba vectơ
,
,
đồng phẳng (h.3.14).
Cách khác.
Ta có =
+
= –
+ (
–
)
= – –
– 2
(vì
= 2
)
Vậy = – 2
– 2
. Hệ thức này chứng tỏ rằng ba vectơ
,
,
đồng phẳng.
C. CÂU HỎI VÀ BÀI TẬP
3.1. Cho hình lập phương A’B’C’D’ cạnh a. Gọi o và O’ theo thứ tự là tâm của hai hình vuông ABCD và A’B’C’D’.
a) Hãy biểu diễn các vectơ ,
theo các vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương đã cho.
b) Chứng minh rằng +
+
’ =
⇒ Xem đáp án tại đây.
3.2. Trong không gian cho điểm O và bốn điểm A, B, C, D phân biệt và không thẳng hàng. Chứng minh rằng điều kiện cần và đủ để bốn điểm A, B, C, D tạo thành một hình bình hành là :
+
=
+
.
⇒ Xem đáp án tại đây.
3.3. Cho tứ diện Gọi p và Q lần lượt là trung điểm của các cạnh AB và CD. Trên các cạnh AC và BD ta lần lượt lấy các điểm M, N sao cho
![]()
Chứng minh rằng ba vectơ ,
,
đồng phẳng.
⇒ Xem đáp án tại đây.
3.4. Cho hình lăng trụ tam giác ABC.A’B’C’ có độ dài cạnh bên bằng a. Trên các cạnh bên ẠA\’, BB’, CC’ ta lấy tương ứng các điểm M, N, p sao cho AM + BN + CP = a.
Chứng minh rằng mặt phẳng (MNP) luôn luôn đi qua một điểm cố định.
⇒ Xem đáp án tại đây.
3.5. Trong không gian cho hai hình bình hành ABCD và AB’C’D’ chỉ có chung nhau một điểm A. Chứng minh rằng các vectơ ,
,
đồng phẳng.
⇒ Xem đáp án tại đây.
3.6. Trên mặt phẳng (à) cho hình bình hành . về một phía đối với mặt phẳng (à) ta dựng hình’bình hành
. Trên các đoạn
ta lần lượt lấy các điểm A, B, C, D sao cho
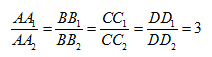
Chứng minh rằng tứ giác ABCD là hình bình hành.
⇒ Xem đáp án tại đây.
3.7. Cho hình hộp ABCD.A’B’C’D’ có P và R lần lượt là trung điểm các cạnh AB và A’D’. Gọi P’, Q, Q’, R’ lần lượt là tâm đối xứng của các hình bình hành ABCD, CDD’C’ , A’B’C’D’, ADD’A’
a) Chứng minh rằng +
+
=
b) Chứng minh hai tam giác PQR và P’Q’R’ có trọng tâm trùng nhau.
⇒ Xem đáp án tại đây.











