Trong bài viết dưới đây, Quantrimang.com sẽ giới thiệu và chia sẻ chi tiết tới bạn đọc một số nội dung liên quan đến chủ đề công thức tính thể tích hình nón, diện tích xung quanh và toàn phần hình nón. Mời các bạn cùng tham khảo.
Hình chóp được tạo thành khi xoay một tam giác vuông quanh trục của nó (một cạnh góc vuông) một vòng.
Tính diện tích hình nón
Diện tích hình nón thường được nhắc đến với 2 khái niệm: xung quanh và toàn phần.
- Diện tích xung quanh hình nón chỉ bao gồm diện tích mặt xung quanh, bao quanh hình nón, không gồm diện tích đáy.
- Diện tích toàn phần được tính là độ lớn của toàn bộ không gian hình chiếm giữ, bao gồm cả diện tích xung quanh và diện tích đáy tròn.
Cụ thể như sau:
Có tam giác ABO vuông tại O, quay một vòng quanh cạnh góc vuông OA cố định thì được một hình nón.
Công thức tính diện tích xung quanh: bằng một nửa tích của chu vi đường tròn đáy và độ dài đường sinh.
 | Áp dụng với ví dụ cụ thể ở trên thì là:
Trong đó:
|
Công thức tính diện tích toàn phần: bằng diện tích xung quanh cộng với diện tích của đáy.
Tính thể tích hình nón
Thể tích hình nón là lượng không gian mà hình nón chiếm.
Công thức tính thể tích hình nón: bằng 1/3 diện tích của mặt đáy nhân với chiều cao

Trong đó:
Vlà thể tích hình nón.rlà bán kính đáy ủa hình nón.hlà chiều cao, khoảng cách giữa đỉnh và đáy của hình nón.
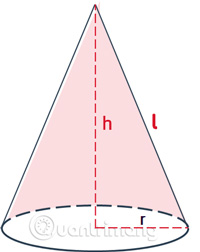
Xác định đường sinh, đường cao và bán kính đáy
Đường cao là khoảng cách từ tâm mặt đáy đến đỉnh của hình chóp.
Đường sinh là khoảng cách từ 1 điểm bất kỳ trên đường tròn đáy đến đỉnh của hình chóp.
Do hình nón được tạo thành khi quay một tam giác vuông quanh trục một cạnh góc vuông của nó một vòng, nên có thể coi đường cao và bán kính đáy là 2 cạnh góc vuông của tam giác, còn đường sinh là cạnh huyền.
Do đó, khi biết đường cao và bán kính đáy, ta có thể tính được đường sinh bằng công thức:
![]()
Biết đường cao và đường sinh, tính bán kính đáy theo công thức:
![]()
Trên đây là các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của hình nón. Cảm ơn các bạn đã theo dõi bài viết.











