Cách tính thể tích hình trụ, diện tích hình trụ
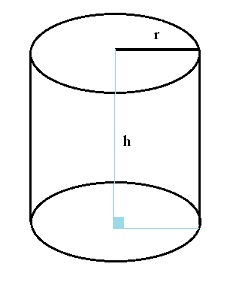
Công thức tính thể tích hình trụ: V = π x r2 x h
Trong đó:
- r: bán kính hình trụ
- h: chiều cao hình trụ
Công thức tính thể tích hình trụ, diện tích xung quanh và toàn phần hình trụ tròn cùng các ví dụ trực quan cho các bạn nắm được cách tính thể tích, diện tích xung quanh và toàn phần của hình trụ áp dụng vào các bài toán và ứng dụng thực tế. Mời các bạn cùng tham khảo.
- Công thức tính chu vi hình tròn và diện tích hình tròn
- Công thức tính thể tích hình lập phương, diện tích hình lập phương
Hình trụ là gì?
Khi quay hình chữ nhật ABCD một vòng quanh cạnh CD cố định ta thu được một hình trụ.
– Hai đáy là hình tròn bằng nhau và nằm trên hai mặt phẳng song song.
– DC là trục của hình trụ.
– Các đường sinh của hình trụ( chẳng hạn EF) vuông góc với hai mặt đáy.
Độ dài đường sinh cũng là độ dài đường cao của hình trụ.
Hình trụ được sử dụng khá phổ biến trong các bài toán hình học từ căn bản đến phức tạp, trong đó công thức tính diện tích, thể tích hình trụ thường được sử dụng khác phổ biến trong việc tính một không gian nhất định bị chiếm giữ bởi một hình trụ.
Bên cạnh đó, công thức tính diện tích, thể tích hình trụ cũng được áp dụng trong các dạng bài toán phức hợp thêm cách tính thể tích hình lập phương hay diện tích hình chữ nhật. Cùng tham khảo công thức tính thể tích hình trụ và các ví dụ trực quan nhất trong cách tính diện tích, thể tích hình trụ.
Công thức và cách tính diện tích hình trụ
Diện tích hình trụ là toàn bộ không gian chiếm giữ bằng cách tính tổng diện tích xung quanh và diện tích hai đáy. Trong khi đó, diện tích toàn phần hình trụ là diện tích của mặt xung quanh hình trụ, không gồm diện tích hai đáy.
1. Công Thức Tính Diện Tích Xung Quanh Hình Trụ
Sxung quanh = 2 x π x r x h
Trong đó:
+ r: bán kính hình trụ
+ h: chiều cao nối từ đáy tới đỉnh hình trụ
2. Công Thức Tính Diện Tích Toàn Phần Hình Trụ
S toàn phần = 2 x π x r2 + 2 x π x r x h = 2 π x r x (r + h)
Trong đó:
+ r: bán kính hình trụ
+ 2 x π x r x h: diện tích xung quanh hình trụ
+ 2 x π x r2: diện tích của hai đáy
3. Ví Dụ Cách Tính Diện Tích Hình Trụ
Ví dụ 1: Cho một hình trụ có bán kính đường tròn đáy là 6 cm, trong khi đó chiều cao nối từ đáy tới đỉnh hình trụ dày 8 cm. Hỏi diện tích xung quanh và diện tích toàn phần của hình trụ bằng bao nhiêu?
Hướng dẫn:
Diện tích xung quanh của hình trụ: Sxq = 2 x π x r x h
Diện tích toàn phần của hình trụ: Stp = 2 x π x r2 + 2 x π x r x h = 2 π x r x (r + h)
Lời giải:
Theo công thức ta có bán đường tròn đáy r = 6 cm và chiều cao của hình trụ h = 8 cm. Suy ra ta có công thức tính diện tích xung quanh hình trụ và diện tích toàn phần hình trụ bằng:
Diện tích xung quanh hình trụ = 2 x π x r x h = 2 x π x 6 x 8 = ~ 301 cm2
Diện tích toàn phần hình trụ = 2 π x r x (r + h) = 2 X π x 6 x (6 + 8) = ~ 527 cm2.
Ví dụ 2: Cho hình trụ có chiều cao 5cm bán kính đáy bằng 3cm. Tính diện tích xung quanh, diện tích toàn phần của hình trụ?
Lời giải:
Diện tích xung quanh của hình trụ: Sxq = 2 x π x r x h = 2 x π x 3 x 5 = 30 π ~ 94,25 cm2
Diện tích toàn phần của hình trụ: Stp = 2 x π x r x (r + h) = 2 x π x 3 x (3 + 5) = 48 π ~ 150,8 cm2
Công thức và cách tính thể tích hình trụ
Thể tích hình trụ là lượng không gian được chiếm giữ một hình trụ nhất định. Thể tích hình trụ sử dụng đơn vị đo là lập phương của khoảng cách (mũ 3 khoảng cách).
1. Công thức tính thể tích hình trụ
V = π x r2 x h
Trong đó:
- r: bán kính hình trụ
- h: chiều cao hình trụ
2. Ví dụ cách tính thể tích của hình trụ
Ví dụ 1: Cho một lăng trụ bất kỳ có bán kính mặt đáy r = 4 cm, trong khi đó, chiều cao nối từ đỉnh của hình trụ xuống đáy hình trụ có độ dài h = 8 cm. Hỏi thể tích của hình trụ này bằng bao nhiêu?
Hướng dẫn:
Công thức tính thể tích hình trụ: V = π x r2 x h
Lời giải:
Theo đó, ta áp dụng vào công thức tính thể tích hình trụ và có: bán kính mặt đáy hình trụ r = 4cm và chiều cao hình trụ h = 8cm. Suy ra, ta có công thức tính thể tích hình trụ như sau:
V = π x r2 x h = π x 42 x 8 = ~ 402 cm3
Ví dụ 2: Một hình trụ có chu vi đáy bằng 20 cm, diện tích xung quanh bằng 14 cm2. Tính chiều cao của hình trụ và thể tích của hình trụ.
Lời giải:
Diện tích xung quanh của hình trụ: Sxq = chu vi đáy x chiều cao = 2 x π x r x h = 20 x h = 14
→ h = 0,7 (cm)
Chu vi đáy bằng 20cm → 2 x π x r = 20 → r ~ 3,18 cm
Thể tích của hình trụ: V = π x r2 x h ~ 219,91 cm3
Ví dụ 3: Một hình trụ có diện tích toàn phần gấp 2 lần diện tích xung quanh biết bán kính đáy hình trụ là 6cm. Tính thể tích hình trụ.
Lời giải:
Diện tích toàn phần gấp 2 lần diện tích xung quanh: Stp = 2Sxq
→ 2 x 2 x π x r x h = 2 x π x r x (r + h) → 2h = 6 + h → h = 6 (cm)
Thể tích của hình trụ: V = π x r2 x h ~ 678,58 cm3











