Bài viết lách sau đây tiếp tục chỉ dẫn chúng ta, những em học viên công thức tính chu vi hình bình hành. Cách tính chu vi hình bình hành giản dị, dễ dàng học tập dễ dàng ghi nhớ vì như thế đấy là một hình đặc biệt quan trọng. Mời chúng ta, những em học viên theo gót dõi.
Hình bình hành là 1 trong những tình huống đặc biệt quan trọng của hình thang, hình bình hành được tạo thành vì như thế 2 cặp cạnh đối tuy vậy song cùng nhau hoặc 1 cặp cạnh đối tuy vậy song và đều bằng nhau. Hình bình hành đem tương đối đầy đủ những đặc thù của hình thang ngoại giả hình bình hành còn tồn tại những đặc thù đặc thù khác ví như nhị góc đối đều bằng nhau, 2 lối chéo cánh hạn chế nhau bên trên trung điểm của từng lối. Nếu chúng ta, những em học viên ko ghi nhớ công thức tính chu vi hình bình hành thì nên tìm hiểu thêm nội dung bài viết sau đây sẽ được chỉ dẫn nhé.
Bạn đang xem: [TaiMienPhi.Vn] Công thức tính chu vi hình bình hành, có ví dụ minh họa
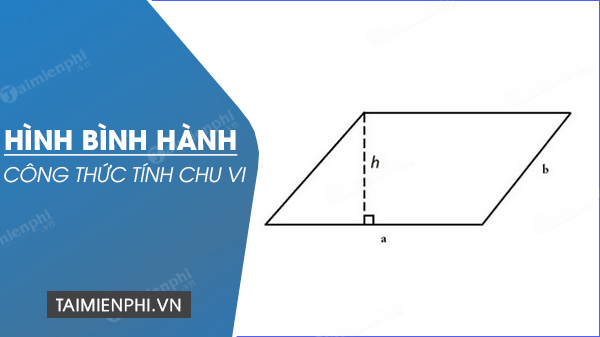
Cách tính chu vi hình bình hành
Nếu như chúng ta hiểu thiếu hiểu biết về hình bình hành thì hoàn toàn có thể tìm hiểu thêm bên trên Wikipedia bài viết lách về hình bình hành này.
Công thức tính chu vi hình bình hành
Chúng tao với 1 hình bình hành ABCD như hình vẽ.
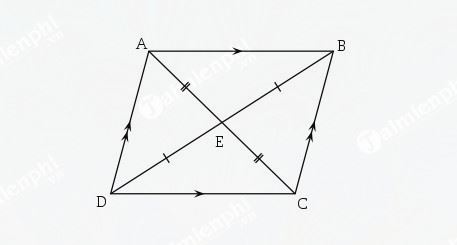
1. Công thức tính chu vi hình bình hành
Vì hình bình hành với 2 cặp cạnh đối tuy vậy song và đều bằng nhau nên chu vi hình bình hành tiếp tục vì như thế gấp đôi tổng 2 cạnh kề nhau, ví dụ tao với công thức
Cách tính chu vi hình bình hành là nhị thứ tự tổng 2 cạnh kề cùng nhau hoặc tổng 4 cạnh của hình thoi.
C = 2 x (a + b)
Trong đó:
- C: Chu vi.
- a, b: 2 cạnh kề nhau của hình bình hành.
2. Ví dụ minh họa tính chu vi hình bình hành
Bài 1: Tính chu vi hình bình hành ABCD phía trên biết AB = 7cm, BC = 5cm
Bài giải: Áp dụng công thức tính chu vi hình bình hành, tất cả chúng ta tiếp tục có
Xem thêm: Chu vi hình chữ nhật lớp 4: Tổng hợp kiến thức và bài tập tính chu vi hay nhất
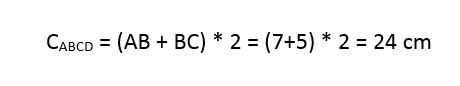
Bài 2: Cho hình bình hành ABCD với chu vi là 26cm, cạnh a của hình ABCD = 6cm. Tính cạnh b của hình bình hành.
Bài giải
Chu vi hình bình hành là C = 2 x (a + b)
=> b = C/2 - a = 26/2 - 6 = 7cm.
Đáp án: cạnh mặt mày của hình bình hành là 7cm.
3. Phương pháp ghi nhớ công thức tính chu vi hình bình hành
Để ghi nhớ được công thức và vận dụng thuần thục trong những bài xích tập dượt thì chúng ta ngoài thực hiện bài xích tập dượt thông thường xuyên, chúng ta cũng có thể ghi nhớ mẹo công thức sau:
Bình hành diện tích S tính sao
Chiều cao nhân lòng đi ra ngay tắp lự khó khăn chi
Chu vi thì có nhu cầu các gì
Cạnh kề nằm trong lại tao ngay tắp lự nhân nhị.
4. Lưu ý Lúc bắt gặp bài xích tập dượt tính chu vi hình bình hành
- quý khách cần thiết xem xét cho tới đơn vị chức năng đo nhập bài xích. Quy thay đổi trở nên một đơn vị chức năng nhằm thực hiện bài xích hiệu suất cao, đúng chuẩn.
- Sau Lúc thực hiện bài xích cần thiết ghi thành quả đáp án tìm kiếm ra.
Xem thêm: Hình avatar buồn, phụ nữ khóc đầy cảm xúc
Trên đấy là chỉ dẫn công thức tính chu vi hình bình hành, công thức dễ dàng ghi nhớ dễ dàng học tập vì như thế hình bình hành là 1 trong những hình đặc biệt quan trọng đúng không nhỉ này. Hy vọng với nội dung bài viết bên trên, những em học viên hoàn toàn có thể vận dụng công thức tính chu vi hình hành nhập vấn đề thực tiễn.
Hình chữ nhật là 1 trong những hình bình hành đặc biệt quan trọng Lúc nhưng mà những cạnh kề của chính nó vuông góc cùng nhau, chúng ta, những em học viên hoàn toàn có thể thấy công thức tính chu vi hình chữ nhật cũng tiếp tục giống như với công thức tính chu vi hình bình đấy nhé.
https://beyeu.edu.vn/cong-thuc-tinh-chu-vi-hinh-binh-hanh-34047n.aspx
Nếu đang được học tập về lối tròn trĩnh, chúng ta tìm hiểu thêm thêm thắt nội dung bài viết share Công thức tính diện tích S hình tròn bên trên phía trên.