Top 100+ hình nền đen đẹp, buồn, tâm trạng 3D chất lượng nhất
Tổng hợp 100+ hình nền đen đẹp, buồn, tâm trạng 3D chất lượng cao sắc nét 4K. Lựa ngay các ảnh hình nền màu đen phù hợp nhất cho bạn
Trong bất kì một câu hỏi này thì công thức toán học tập là cốt lõi khiến cho bạn tìm kiếm ra đáp án nhanh nhất có thể. Công thức tính diện tích S giác vuông, đều, tam giác cân nặng chắc chắn rất gần gũi gì so với từng người. Tuy nhiên so với từng hình lại sở hữu những cơ hội tích diện tích S (S) không giống nhau nhưng mà nhập nội dung bài viết tại đây Cửa Hàng chúng tôi tiếp tục khiến cho bạn thực hiện rõ rệt nhé!
1. Công thức tính diện tích S tam giác
1.1 Công thức tính diện tích S tam giác thường
Giống như thật nhiều câu hỏi không giống, thì câu hỏi tính diện tích tam giác cũng sẽ sở hữu những công thức nhưng mà bạn phải học tập. Và Khi đang được sở hữu công thức nhằm vận dụng thì bất kể câu hỏi tính diện tích S tam giác này các bạn cũng tiếp tục rất có thể hoàn thiện dễ dàng và đơn giản. Đối với những loại tam giác thông thường lúc này sở hữu thật nhiều công thức tính diện tích S tam giác.
Tuy nhiên, sẽ sở hữu những công thức tính diện tích S tính tam giác không giống nhau tùy nằm trong vào cụ thể từng fake thiết của đề bài bác. Xem đề bài bác cho tới những gì nhằm kể từ cơ tất cả chúng ta rất có thể vận dụng từng công thức cho tới thích hợp nhất. Cụ thể sở hữu những công thức tính diện tích tam giác vuông, đều, cân nặng như sau:
1.2 Công thức diện tích S tam giác đều
Tam giác đều là tam giác thông thường tuy nhiên điểm nhất là có tính nhiều năm 3 cạnh đều đều bằng nhau và toàn bộ những góc nhập tam giác đều vị 60 phỏng. Theo cơ, diện tích tam giác đều được xem vị công thức nhau sau: S = ½. A2. sin 60o = A2. (3 /4). Trong số đó A đó là cạnh của tam giác đều.
1.3 Công thức diện tích S tam giác vuông
Tam giác vuông là tam giác có một góc vuông, cách tính diện tích tam giác vuông cũng cực kỳ giản dị và đơn giản, nó là tình huống đặc biệt quan trọng của phương pháp tính diện tích S tam giác thông thường lúc biết 2 cạnh và góc xen thân thiết. Khi cơ sin 90O = 1 và diện tích tam giác vuông được xem như sau: S= ½ ab, nhập cơ a, b đó là phỏng nhiều năm ứng của 2 cạnh góc vuông
Cách tính S tam giác vuông cân nặng đơn giản
1.4 Công thức diện tích S tam giác cân
Tam giác cân nặng có tính nhiều năm 2 cạnh đều bằng nhau gọi là 2 cạnh mặt mũi, phỏng nhiều năm còn sót lại là cạnh lòng, ngoại giả còn tồn tại 2 cạnh lòng đều bằng nhau. Do cơ, diện tích tam giác cân sẽ tiến hành tính vị 1/2 độ cao nhân cạnh lòng ứng chiếu lên.
Ngoài rời khỏi, tam giác cân nặng lại sở hữu tình huống đặc biệt quan trọng của riêng rẽ nó được gọi là tam giác vuông cân nặng. Khi cơ 2 cạnh góc vuông tiếp tục đều bằng nhau và diện tích tam giác vuông cân sẽ tiến hành tính vị ½ a2, nhập cơ a đó là phỏng nhiều năm của cạnh góc vuông cân nặng.
2. Một số dạng toán tính diện tích S tam giác
2.1 Cách tính diện tích S tam giác nhập hệ tọa phỏng Oxyz
Trong quy trình học tập tất cả chúng ta gặp gỡ thật nhiều dạng bài bác luyện không giống nhau. Và nhập hệ trục tọa phỏng Oxyz cũng có thể có công thức tính riêng rẽ nhưng mà chúng ta nên biết. Cách tính diện tích S tam giác nhập hệ tọa phỏng Oxyz là: SABC= ½ [AB;AC]
Trong cơ [AB;AC] được xem như sau:
Gọi tọa phỏng điểm A là A (a1, b1, c1); tọa phỏng điểm B là B (a2, b2, c2); tọa phỏng điểm C là C (a3, b3, c2). Theo cơ, AB = (a2-a1; b2-b1; c2-c1); AC = (a3-a1; b3-b1; c3-c1). Từ cơ tớ sở hữu cơ hội tính: [AB;AC]= ( b2−b1 c2−c1) b3−b1 c3−c1 ; c2−c1 a2−a1 c3−c1 a3−a1; ; a2−a1 b2−b1 a3−a1 b3−b1 )
Sau cơ tất cả chúng ta trừ chéo cánh từng biểu thức lẫn nhau sẽ sở hữu được thành phẩm của [AB;AC] là tọa phỏng bao gồm 3 điểm nhé.
2.2 Tính diện tích S lúc biết cạnh lòng và chiều cao
Đối với fake thiết cho thấy độ cao và cạnh lòng thì diện tích tam giác sẽ tiến hành tính vị 1/2 độ cao cơ nhân với cạnh lòng ứng chiếu lên. Đây là công thức tính diện tích S tam giác thường thì nhưng mà tất cả chúng ta thông thường gặp gỡ nhất. Tuy nhiên, tất cả chúng ta cũng nên nên biết một vài ba công thức tính diện tích S thời gian nhanh tại đây nhằm thuận tiện cho tới việc đo lường và tính toán đạt thành phẩm nhanh nhất có thể.
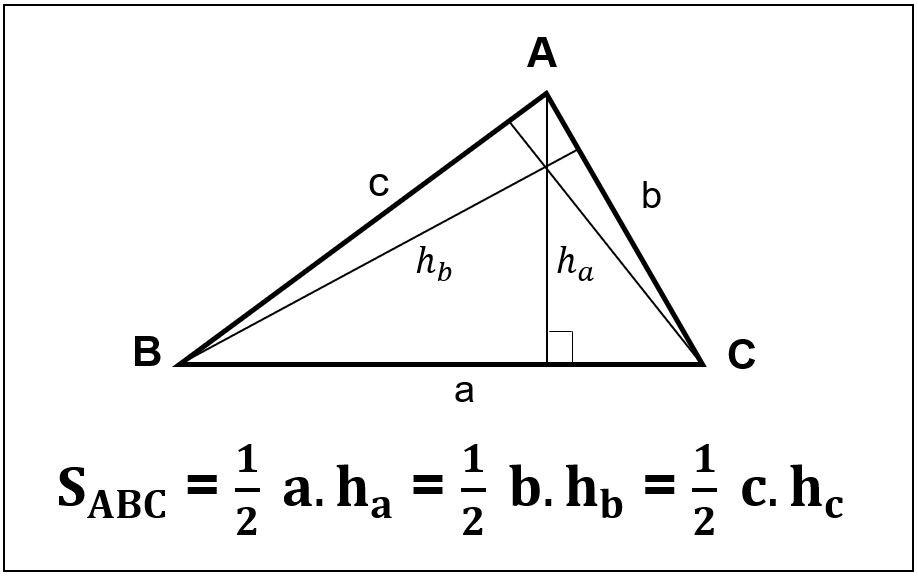
Tính diện tích S lúc biết cạnh lòng và chiều cao
2.3 Tính diện tích S tam giác tùy theo 2 cạnh và góc xen giữa
Nếu fake thiết cho tới 2 cạnh của một tam giác và góc xen thân thiết thì diện tích S của tam giác cũng rất có thể được xem vị công thức như sau. Diện tích tam giác vị 1/2 tích 2 cạnh nhân với lại sin của góc xen thân thiết nhì cạnh cơ.
2.4 Giả thiết đề bài bác cho tới chu vi và nửa đường kính lối tròn xoe nội tiếp
Đối với tình huống đề bài bác cho tới chu vi và nửa đường kính lối tròn xoe thì các bạn sở hữu thể tính diện tích S tam giác này bằng phương pháp tại đây. Ta được xem là lấy nửa chu vi tam giác (p) nhân với lại nửa đường kính lối tròn xoe nội tiếp (r) thì vị diện tích tam giác cần thiết tính.
Xem thêm: Công thức tính nửa chu vi hình chữ nhật và bài tập có lời giải từ A – Z
2.5 Diện tích tam giác theo dõi phỏng nhiều năm 3 cạnh và nửa đường kính lối tròn xoe nước ngoài tiếp
Chúng tớ cũng nên rất là chú ý công thức này Khi giải bài bác luyện. Diện tích hình tam giác sẽ tiến hành tính vị tích phỏng nhiều năm của 3 cạnh, toàn bộ lấy chi cho tới 4 thứ tự nửa đường kính của lối tròn xoe nước ngoài tiếp tam giác (4R).
Ngoài rời khỏi tất cả chúng ta còn tồn tại cách tính diện tích S hình tam giác vị công thức Hê – rông:
SABC= pp−ap−b(p−c)
Trong đó: a, b, c theo lần lượt là phỏng nhiều năm của 3 cạnh và p đó là nửa chu vi của tam giác nhé!
3. Một số dạng toán tính diện tích S tam giác
Sau phía trên Cửa Hàng chúng tôi tiếp tục cung ứng cho mình những ví dụ về một vài câu hỏi tính diện tích S tam giác. Đồng thời là giải pháp vận dụng và đo lường và tính toán dựa vào những công thức sở hữu bên trên thực tiễn nhằm rất có thể thể hiện cho mình một vài ví dụ nhằm rất có thể dễ dàng tưởng tượng đo lường và tính toán nhé!
3.1 Bài toán tính diện tích tam giác vuông
Giả thiết đề bài bác cho tới tam giác ABC vuông bên trên A, nhập cơ có tính nhiều năm nhì cạnh BA và CA theo lần lượt là 3 centimet và 4 centimet. Yêu cầu tính diện tích tam giác vuông ABC?
Theo công thức phía trên đang được ra mắt, diện tích S vuông ABC sẽ tiến hành tính vị ½. 3.4= 6 cm2
Các các bạn chú ý nếu như đề bài bác chỉ cho tới cạnh huyền và một cạnh góc vuông và cho thấy trước diện tích tam giác, đòi hỏi tính cạnh còn sót lại thì kể từ công thức thuở đầu tính diện tích S tất cả chúng ta rất có thể duy luôn luôn rời khỏi được cạnh còn sót lại nhé!
3.2 Bài toán tính diện tích S tam giác đều
Bài toán cho tới tam giác ABC đều những cạnh của tam giác (a) vị 3. Tính diện tích S tam giác.
Áp dụng công thức tính S = ½. A2. sin 60o = A2. (3 /4) tớ sở hữu SABC= 32. (3 /4) = 93 /4
Bài toán tính S tam giác đều
3.3 Bài toán tính diện tích S nhập hệ tọa phỏng Oxyz
Trong không khí Oxyz cho tới 3 điểm D (1;2;1), E (2;-1;3), F (5;2;-3). Tính diện tích S của tam giác nhập hệ tọa phỏng.
DE = (1; -3; 2); DF = (4; 0; -4)
Xem thêm: Tính chất hóa học của Metan CH4 | Tính chất vật lí, nhận biết, điều chế, ứng dụng.
[DE;DF]= ( −3 2 0 −4 ; 2 1 −4 4 ; 1 −3 4 0 ) = (10; 12; 13)
Suy rời khỏi SDEF= ½ [DE;DF] = ½. 102+122+132 = 413/2
Như vậy, nội dung bài viết bên trên đang được khiến cho bạn hấp thụ thêm những kỹ năng hữu dụng về công thức diện tích S tam giác bao hàm công thức tính diện tích S giác vuông, đều, tam giác cân. Mong rằng với những vấn đề nhưng mà Cửa Hàng chúng tôi cung ứng các bạn sẽ rất có thể học tập môn toán và sở hữu một điểm toán rất tốt. Hãy theo dõi dõi Cửa Hàng chúng tôi nhằm hiểu biết thêm nhiều điều hữu dụng rộng lớn nhé.