Bài 5: Thể tích khối trụ

I. Lý thuyết
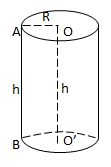
\(V=\pi .R^2.h\)
(=S_đáy.h)
R: bán kính đáy
h: chiều cao (k/c giữa hai đáy = OO')

II. Bài tập
Ví dụ 1: Tính thể tích của khối trụ biết khoảng cách giữa hai tâm đáy là a (cm) và đường kính của đáy là b(cm)

Giải
\(2R=b\Rightarrow R=\frac{b}{2}\)
\(h=OO'=a\)
\(V=\pi .R^2.h=\pi =\frac{b^2}{4}.a=\frac{ab^2}{4}\pi (cm^3)\)
Ví dụ 2: Cho hình chữ nhật ABCD có AC = 10cm, AB=6cm. Cho đường gấp khúc ABCD quay quanh AD ta được 1 hình trụ. Tính thể tích khối trụ được giới hạn bởi hình trụ trên.

Giải

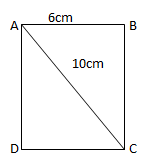
Trong tam giác ABC
\(h=BC=\sqrt{AC^2-AB^2}=\sqrt{10^2-6^2}=8(cm)\)
\(V=\pi .R^2.h=\pi .6^2.8=288.\pi (cm^3)\)

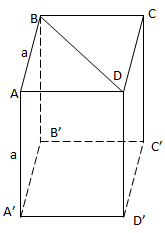
Ví dụ 3: Cho hình lập phương ABCD.A'B'C'D' có AB = a. Tính thể tích của khối trụ có đáy là 
a) Đường trọn ngoại tiếp ABCD, A'B'C'D'
b) Đường trọn nội tiếp ABCD, A'B'C'D'

Giải
a) Bán kính đường tròn ngoại tiếp hình vuông ABCD là
\(R_1=\frac{1}{2}BD=\frac{1}{2}.a\sqrt{2}\)
\(V=\pi .R_1^2.h=\pi .\frac{a^2}{2}.a=\frac{\pi a^3}{2}\) (đvtt)

b) Bán kính của đường tròn nội tiếp hình vuông ABCD là 

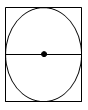
\(R_2=\frac{1}{2}AB=\frac{a}{2}\)

\(V=\pi .R_2^2.h=\pi .\frac{a^2}{4}.a=\frac{\pi a^3}{4}\) (đvtt)