Đường trung tuyến là gì? Tính chất, công thức tính đường trung tuyến
Đường trung tuyến: Tính chất, công thức tính đường trung tuyến, Đường trung tuyến là tài liệu hữu ích được biên soạn đầy đủ lý thuyết về khái niệm, công thức tính
1. Định nghĩa Đường trực tiếp d được gọi là vuông góc với mặt mày phẳng lặng (P) nếu như đường thẳng liền mạch d vuông góc với từng đường thẳng liền mạch a ở trong mặt mày phẳng lặng (P), kí hiệu \(d \bot \left( P.. \right)\) hoặc \(\left( P.. \right) \bot d\).
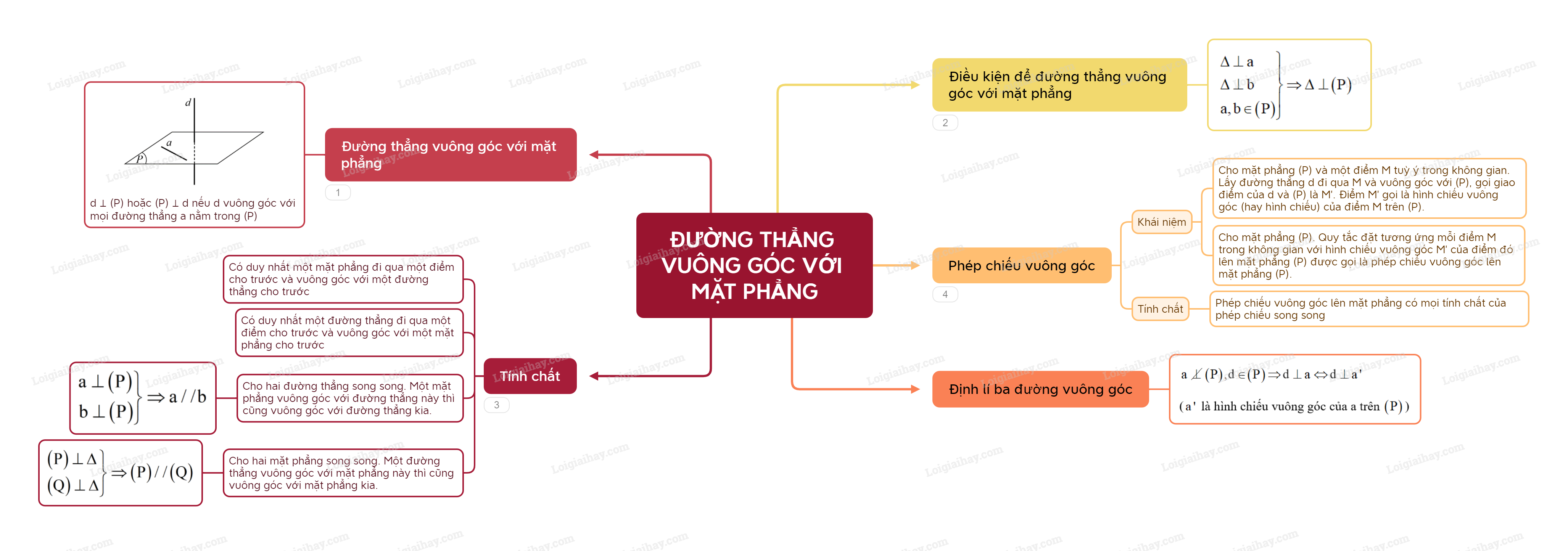
1. Định nghĩa
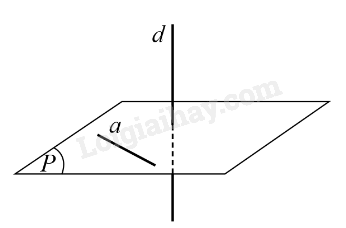
Đường trực tiếp d được gọi là vuông góc với mặt mày phẳng lặng (P) nếu như đường thẳng liền mạch d vuông góc với từng đường thẳng liền mạch a ở trong mặt mày phẳng lặng (P), kí hiệu \(d \bot \left( P.. \right)\) hoặc \(\left( P.. \right) \bot d\).
Bạn đang xem: Lý thuyết Đường thẳng vuông góc với mặt phẳng - Toán 11 Cánh diều | SGK Toán 11 - Cánh diều
2. Điều khiếu nại nhằm đường thẳng vuông góc với mặt phẳng
Nếu một đường thẳng liền mạch vuông góc với hai tuyến phố trực tiếp hạn chế nhau nằm trong lệ thuộc một phía phẳng lặng thì nó vuông góc với mặt mày phẳng lặng ấy.
Nhận xét: Ta rất có thể chứng tỏ hai tuyến phố trực tiếp vuông góc bằng phương pháp chứng tỏ một đường thẳng liền mạch vuông góc với một phía phẳng lặng chứa chấp đường thẳng liền mạch cơ.
3. Tính chất
- Tính hóa học 1: Có độc nhất một phía phẳng lặng trải qua một điểm cho tới trước và vuông góc với 1 đường thẳng liền mạch cho tới trước.
- Tính hóa học 2: Có độc nhất một đường thẳng liền mạch trải qua một điểm cho tới trước và vuông góc với một phía phẳng lặng cho tới trước.
4. Liên hệ thân thích mối quan hệ tuy vậy song và mối quan hệ vuông góc của đường thẳng liền mạch và mặt mày phẳng
- Tính hóa học 3:
Cho hai tuyến phố trực tiếp tuy vậy tuy vậy. Một mặt mày phẳng lặng vuông góc với đường thẳng liền mạch này thì cũng vuông góc với đường thẳng liền mạch cơ.
Hai đường thẳng liền mạch phân biệt nằm trong vuông góc với một phía phẳng lặng thì tuy vậy song cùng nhau.
- Tính hóa học 4:
Cho nhì mặt mày phẳng lặng tuy vậy tuy vậy. Một đường thẳng vuông góc với mặt phẳng này thì cũng vuông góc với mặt mày phẳng lặng cơ.
Hai mặt mày phẳng lặng phân biệt nằm trong vuông góc với 1 đường thẳng liền mạch thì tuy vậy song cùng nhau.
5. Phép chiếu vuông góc
Cho mặt mày phẳng lặng (P) và một điểm M tuỳ ý nhập không khí. Lấy đường thẳng liền mạch d trải qua M và vuông góc với (P), gọi giao phó điểm của d và (P) là M’. Điểm M’ gọi là hình chiếu vuông góc (hay hình chiếu) của điểm M bên trên (P).
Xem thêm: Tất cả công thức lý 11 học kì 1 : Những kiến thức cơ bản mà bạn cần nắm vững
Cho mặt mày phẳng lặng (P). Quy tắc bịa ứng từng điểm M nhập không khí với hình chiếu vuông góc M’ của điểm cơ lên phía trên mặt phẳng lặng (P) được gọi là phép chiếu vuông góc lên phía trên mặt phẳng lặng (P).
Nhận xét: Vì quy tắc chiếu vuông góc là một trong tình huống đặc trưng của quy tắc chiếu tuy vậy song (khi phương chiếu vuông góc với mặt mày phẳng lặng chiếu) nên quy tắc chiếu vuông góc sở hữu rất đầy đủ những đặc điểm của quy tắc chiếu tuy vậy tuy vậy.
6. Định lí thân phụ lối vuông góc
Cho đường thẳng liền mạch a ko vuông góc với mặt mày phẳng lặng (P) và đường thẳng liền mạch d ở trong mặt mày phẳng lặng (P). Khi cơ, d vuông góc với a Lúc và chỉ Lúc d vuông góc với hình chiếu a’ của a bên trên (P).
Bình luận
Chia sẻ
-
Giải hoạt động và sinh hoạt mở màn trang 80 SGK Toán 11 tập luyện 2 – Cánh Diều
Trong Hình 9, cột mộc trực tiếp đứng và sàn ngôi nhà ở ngang khêu nên hình hình ảnh đường thẳng vuông góc với mặt phẳng.
-
Giải mục 1 trang 80 SGK Toán 11 tập luyện 2 - Cánh Diều
Hình 10 tế bào miêu tả một người thợ thuyền xây đang được thả chạc dọi vuông góc với nền ngôi nhà.
-
Giải mục 2 trang 81 SGK Toán 11 tập luyện 2 - Cánh Diều
Hình 12 tế bào miêu tả cửa ngõ tròn xoe xoay, ở cơ trục cửa ngõ và nhì mép cửa ngõ khêu nên hình hình ảnh những đường thẳng liền mạch d
-
Giải mục 3 trang 81, 82 SGK Toán 11 tập luyện 2 - Cánh Diều
Cho điểm O và đường thẳng liền mạch a.
-
Giải mục 4 trang 83, 84 SGK Toán 11 tập luyện 2 - Cánh Diều
Trong Hình 19, nhì thanh Fe và phiên bản phẳng lặng nhằm ngồi khêu nên hình hình ảnh hai tuyến phố trực tiếp a, b và mặt mày phẳng lặng (P).
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Cánh diều - Xem ngay
Xem thêm: Lý thuyết Đường thẳng vuông góc với mặt phẳng - Toán 11 Cánh diều | SGK Toán 11 - Cánh diều
2K7 nhập cuộc tức thì group nhằm nhận vấn đề thi tuyển, tư liệu không tính tiền, trao thay đổi tiếp thu kiến thức nhé!
>> Lộ Trình Sun 2025 - 3IN1 - 1 trong suốt lộ trình ôn 3 kì ganh đua (Luyện ganh đua TN trung học phổ thông & ĐGNL; ĐGTD) bên trên Tuyensinh247.com. Đầy đầy đủ theo đuổi 3 đầu sách, Thầy Cô giáo đảm bảo chất lượng, 3 bước chi tiết: Nền tảng lớp 12; Luyện ganh đua chuyên nghiệp sâu; Luyện đề đầy đủ dạng thỏa mãn nhu cầu từng kì ganh đua.