beyeu
beyeu
Trang chủ Giáo Dục Cung và góc lượng giác: Lý thuyết và các dạng toán lớp 10 - VUIHOC

Cung và góc lượng giác: Lý thuyết và các dạng toán lớp 10 - VUIHOC

Cung và góc lượng giác là dạng bài xích có tương đối nhiều công thức khó khăn, rất dễ khiến cho lầm lẫn vô quy trình thực hiện bài xích tập dượt. Để hoàn toàn có thể chung chúng ta tóm chắc chắn kỹ năng, Vuihoc.vn mang lại nội dung bài viết tổ hợp không hề thiếu về cung và góc lượng giác .

1. Khái niệm công cộng về cung và góc lượng giác

1.1. Cung lượng giác là gì?

Ta cho 1 lối tròn xoe với nửa đường kính R, tâm O, tao tiếp tục lấy nhì điểm phân biệt A và B bên trên lối tròn xoe (O) ê.

Bạn đang xem: Cung và góc lượng giác: Lý thuyết và các dạng toán lớp 10 - VUIHOC

Lúc này tao nói: $\widehat{AmB}$ là cung nhỏ, $\widehat{AnB}$ sẽ là cung rộng lớn. Khi ghi chép $\widehat{AB}$ ta tiếp tục hiểu đấy là cung nhỏ. AB là thừng cung chắn $\widehat{AB}$.

1.2. Góc lượng giác là gì?          

Khi tao với nhì góc với nằm trong tia đầu và tia cuối thì tao với những số đo không giống nhau một bội vẹn toàn $360^{\circ}$ (hay $2\pi$).

Cung và góc lượng giác

1.3. Đường tròn xoe lượng giác

 Đường tròn xoe lượng giác được khái niệm là vô nằm trong mặt mày bằng toạ chừng, tao vẽ lối tròn xoe tâm O, nửa đường kính R, mặt khác tất cả chúng ta lựa chọn điểm A thực hiện gốc và lựa chọn chiều xoay ngược với chiều kim đồng hồ đeo tay là chiều dương.

 Điểm M(x;y) bên trên đường tròn lượng giác, (OA;OM) = α được gọi là vấn đề bên trên đường tròn lượng giác màn trình diễn cung lượng giác với số đo α.

  • Trục Ox gọi là trục độ quý hiếm của cos.

  • Trục Oy gọi là trục độ quý hiếm của sin.

  • Trục At gốc A nằm trong phía với trục Oy gọi là trục độ quý hiếm của tan.

  • Trục Bs gốc B nằm trong phía với trục Ox gọi là trục độ quý hiếm của cot.

 Cung và góc lượng giác và đường tròn lượng giác

Giá trị lượng giác của sin, cosin, tang và cotang:

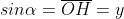
sin\alpha = \overline{OH} = y

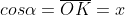
cos\alpha = \overline{OK} = x

tan\alpha = \frac{sin\alpha }{cos\alpha } (\alpha \neq \frac{\pi }{2} + k\pi )

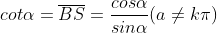
cot\alpha = \overline{BS} = \frac{cos\alpha }{sin\alpha } (a \neq k\pi )

Dấu của những độ quý hiếm lượng giác

Bảng vệt của những độ quý hiếm lượng giác - góc và cung lượng giác

2. Đơn vị đo cung và góc lượng giác

2.1. Đơn vị Radian

Khi cung có tính lâu năm chủ yếu vì như thế nửa đường kính lối tròn xoe với chứa chấp cung ấy và số đo là 

1 radian, kí hiệu 1$rad$ hoặc giản dị và đơn giản là quăng quật $rad$ và kí hiệu là một.

2.2. Đơn vị độ

Độ đó là số đo của góc bằng 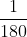\frac{1}{180} góc bẹt.

Số đo của góc ở tâm chắn cung đo thông qua số đo của một cung tròn xoe.

Do ê số đo của cung bằng 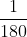\frac{1}{180} nửa lối tròn xoe là một trong chừng.

Kí hiệu 1ođọc là một trong độ 

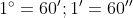
1^{\circ} = 60';1' = 60''

2.3. Đổi chừng rời khỏi Radian

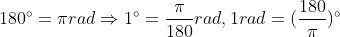
180^{\circ} = \pi rad \Rightarrow 1^{\circ} = \frac{\pi}{180}rad, 1rad = (\frac{180}{\pi})^{\circ}

2.4. Độ lâu năm của một cung tròn        

Một cung của lối tròn xoe nửa đường kính R với số đo rad thì chừng lâu năm l=rad 

Trên một lối tròn xoe với nửa đường kính R, tâm O, chừng lâu năm l của cung n được xem theo đòi công thức: 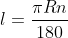l=\frac{\pi R n}{180}

Cung lượng giác và chừng lâu năm cung tròn

Tham khảo tức thì cỗ tư liệu tổng ôn kỹ năng và cách thức giải từng dạng bài xích tập dượt độc quyền của VUIHOC ngay!

3. Bảng độ quý hiếm lượng giác

3.1. Cách mò mẫm độ quý hiếm lượng giác của cung

Cho một trong những thực \alpha. Gọi M là vấn đề ngọn của cung với số đo \alpha trên đường tròn lượng giác. Xét điểm M với tọa chừng là M(x;y). Chúng tao với khái niệm sau: 

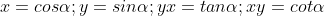
x = cos\alpha ; y=sin\alpha ; yx=tan\alpha; xy=cot\alpha

Giá trị cung và góc lượng giác và báo giá trị lượng giác

Ta với công thức: 

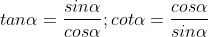
tan\alpha = \frac{sin\alpha }{cos\alpha} ; cot\alpha = \frac{cos\alpha }{sin\alpha}

Ta với một trong những công thức sau: 

  • sina=1 \Leftrightarrow \alpha = \frac{\pi}{\alpha} + k2\pi

  • sina= -1 \Leftrightarrow \alpha = \frac{-\pi}{2} + k2\pi

  • sina=0 \Leftrightarrow \alpha = k\pi

  • cosa=1 \Leftrightarrow \alpha = k2\pi

  • cosa= -1 \Leftrightarrow \alpha = k2\pi

  • cosa=0 \Leftrightarrow \alpha = k\pi

3.2. Giá trị lượng giác của những góc đặc biệt

Cung và góc lượng giác và góc đặc biệt

3.3. Tìm độ quý hiếm lượng giác của những góc liên quan

Góc đối nhau Góc bù nhau Góc phụ nhau
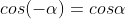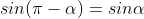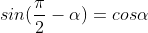cos(-\alpha ) = cos\alpha sin(\pi - \alpha ) = sin\alpha sin(\frac{\pi }{2} - \alpha ) = cos\alpha
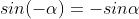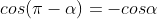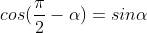sin(-\alpha ) = -sin\alpha cos(\pi - \alpha ) = -cos\alpha cos(\frac{\pi }{2} - \alpha ) = sin\alpha
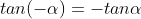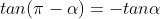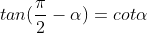tan(-\alpha ) = -tan\alpha tan(\pi - \alpha ) = -tan\alpha tan(\frac{\pi }{2} - \alpha ) = cot\alpha
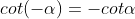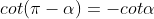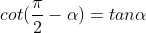cot(-\alpha ) = -cot\alpha cot(\pi - \alpha ) = -cot\alpha cot(\frac{\pi }{2} - \alpha ) = tan\alpha

Công thức nghiệm cơ bản:

Công thức nghiệm cơ bạn dạng của lượng giác

3.4. Các công thức lượng giác

Một số công thức lượng giác

Chi tiết những em học viên hoàn toàn có thể tìm hiểu thêm bài xích viết: Tổng ăn ý công thức lượng giác

PAS VUIHOC – GIẢI PHÁP ÔN LUYỆN CÁ NHÂN HÓA

Khóa học tập online ĐẦU TIÊN VÀ DUY NHẤT:  

⭐ Xây dựng suốt thời gian học tập kể từ rơi rụng gốc cho tới 27+  

⭐ Chọn thầy cô, lớp, môn học tập theo đòi sở thích  

⭐ Tương tác thẳng hai phía nằm trong thầy cô  

⭐ Học đến lớp lại cho tới lúc nào hiểu bài xích thì thôi

⭐ Rèn tips tricks chung tăng cường thời hạn thực hiện đề

⭐ Tặng full cỗ tư liệu độc quyền vô quy trình học tập tập

Đăng ký học tập demo không lấy phí ngay!!

4 .Một số bài xích tập dượt về những dạng toán cung và góc lượng giác lớp 10

4.1. Cung lượng giác bên trên lối tròn xoe được màn trình diễn thế nào?

Phương pháp giải:

Ta hay sử dụng thành quả tiếp sau đây nhằm màn trình diễn được những góc lượng giác bên trên đường tròn lượng giác:

  • Góc \alpha và góc \alpha+k2\pi, k\in Z sẽ với nằm trong điểm màn trình diễn bên trên đường tròn lượng giác.

  • Số điểm bên trên đường tròn lượng giác màn trình diễn vì như thế số đo với dạng \alpha + \frac{k2\pi}{m} (với $k$ là số vẹn toàn và m là số vẹn toàn dương) là m. Từ ê nhằm màn trình diễn những góc lượng giác ê tao theo lần lượt mang đến kể từ k cho tới (m-1) rồi màn trình diễn những góc ê.

Ví dụ: Biểu trình diễn những góc lượng giác với số đo sau: 

Xem thêm: Công thức tính nửa chu vi hình chữ nhật và bài tập có lời giải từ A – Z

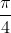
  1. \frac{\pi}{4}

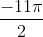
  2. \frac{-11\pi}{2}

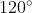
  3. 120^{\circ}

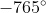
  4. -765^{\circ}

Cách giải: 

1. Ta có: 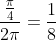\frac{\frac{\pi}{4}}{2\pi} = \frac{1}{8}. Ta phân chia lối tròn xoe rời khỏi những phần cân nhau trở nên tám phần.

Khi ê điểm 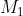M_{1} là điểm màn trình diễn vì như thế góc với số đo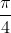 \frac{\pi}{4}

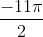2. Ta với \frac{-13\pi}{2} = -2\pi+(-3).2\pi vì thế điểm màn trình diễn vì như thế góc \frac{-11\pi}{2} trùng với góc 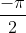\frac{-\pi }{2} và là vấn đề B'.

3. Ta với 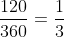\frac{120}{360} = \frac{1}{3}. Khi ê, phân chia lối tròn xoe trở nên tía phần cân nhau thì được điểm M2 là điểm màn trình diễn vì như thế góc với số đo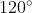 120^{\circ}

4. Ta với -765^{\circ} = -45^{\circ} + (-2). 360^{\circ} do ê điểm màn trình diễn vì như thế góc 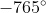-765^{\circ} trùng với góc 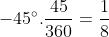-45^{\circ}. \frac{45}{360} = \frac{1}{8}. Khi ê, tao phân chia lối tròn xoe trở nên 8 phần cân nhau (chú ý góc âm).

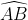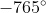Khi ê điểm M3 (điểm vị trí trung tâm cung nhỏ \widehat{AB}) là vấn đề màn trình diễn vì như thế góc với số đo -765^{\circ}.

4.2. Cách xác lập độ quý hiếm của biểu thức chứa chấp góc đặc biệt

Bài toán này với mục tiêu xác lập độ quý hiếm của biểu thức với chứa chấp góc đặc biệt quan trọng và vệt của độ quý hiếm lượng giác của góc lượng giác.

Phương pháp giải: 

  • Sử dụng những khái niệm độ quý hiếm lượng giác vô bài xích.

  • Sử dụng báo giá trị lượng giác đặc biệt quan trọng và đặc điểm. 

  • Sử dụng độ quý hiếm lượng giác của góc tương quan đặc biệt quan trọng và hệ thức lượng giác cơ bạn dạng.

  • Để xác lập được vệt của những độ quý hiếm lượng giác của một cung (góc), tất cả chúng ta vận dụng bảng xét vệt những độ quý hiếm lượng giác. Đồng thời xác lập điểm ngọn của cung (tia cuối của góc) nằm trong phần tư này. 

Ví dụ: 

Bài 1: Tính độ quý hiếm biểu thức lượng giác: 

1. A = sin \frac{7\pi}{6} +cos 9\pi + tan (\frac{-5\pi}{4}) + cot \frac{7\pi}{2}

2. B = \frac{1}{368^{\circ}} + \frac{2sin2550^{\circ}.cos(-188^{\circ})}{2cos638^{\circ} + cos 9 8^{\circ}}

Cách giải: 

1. Ta có:

A = sin (\pi + \frac{\pi}{6}) + cos (\pi + 4.2\pi) - tan(\pi + \frac{\pi}{4})+cot (\frac{\pi}{2} + 3\pi)

A = -sin \frac{\pi}{6} + cos \pi -tan \frac{\pi}{4} + cot \frac{\pi}{2} = \frac{-1}{2} - 1 - 1 + 0 = \frac{-5}{2}

2. Ta có:

B = \frac{1}{tan8^{\circ}} + \frac{2(sin(30^{\circ}+7.360^{\circ})}.cos{8^{\circ}+180^{\circ}}{2cos(-90^{\circ}) + 8^{\circ} + 2 . 360^{\circ} + cos (90^{\circ} + 8^{\circ})}

B= \frac{1}{tan8^{\circ}} + \frac{2sin30^{\circ}.(-cos8^{\circ})}{2cos(8^{\circ}-90^{\circ})-sin8^{\circ}} = \frac{1}{tan8^{\circ}} + \frac{2sin30^{\circ}.(-cos8^{\circ})}{2cos(8^{\circ}-90^{\circ})-sin8^{\circ}}

= \frac{1}{tan8^{\circ}} + \frac{2.\frac{1}{2}.(-cos8^{\circ})}{2cos(90^{\circ}-8^{\circ}) - sin8^{\circ}} = \frac{1}{tan8^{\circ}} - \frac{cos8^{\circ}}{2sin8^{\circ}-sin8^{\circ}}

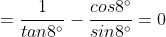
= \frac{1}{tan8^{\circ}} - \frac{cos8^{\circ}}{sin8^{\circ}} = 0

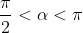Bài 2: Cho \frac{\pi}{2} < \alpha < \pi. Xác ấn định vệt của những độ quý hiếm lượng giác:

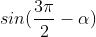
  1. sin (\frac{3\pi}{2} - \alpha)

  2. cos (\alpha + \frac{\pi}{2})

  3. tan (\frac{3\pi}{2} + \alpha)

Cách giải: 

1. Ta có: \frac{\pi}{2} < \alpha < \pi \Rightarrow \pi < \alpha + \frac{\pi}{2} < \frac{3\pi}{2} \Rightarrow -1 < cos (\alpha + \frac{\pi}{2}) < 0

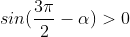
Vậy sin (\frac{3\pi}{2} - \alpha) > 0

2. Ta có:  \frac{\pi}{2} < \alpha < \pi \Rightarrow \pi < \alpha + \frac{\pi}{2} < \frac{3\pi}{2} \Rightarrow -1 < cos (\alpha + \frac{\pi}{2}) < 0.

Vậy cos (\alpha + \frac{\pi}{2})<0

3. \frac{\pi}{2} < \alpha < \pi \Rightarrow 2\pi < \frac{3\pi}{2} + \alpha < \frac{5\pi}{2}

Do ê cos (\frac{3\pi}{2} + \alpha) nằm trong cung phần tư loại I.

Vậy cos (\frac{3\pi}{2} + \alpha) > 0

4.3. Chứng minh biểu thức ko dựa vào góc X, giản dị và đơn giản biểu thức

Đây là dạng chứng tỏ đẳng thức lượng giác, chứng tỏ biểu thức ko tùy theo góc x, giản dị và đơn giản biểu thức.

Phương pháp giải: 

  • Sử dụng những hệ thức lượng giác cơ bạn dạng, những hằng đẳng thức kỷ niệm và dùng đặc điểm của độ quý hiếm lượng giác nhằm đổi khác.

  • Khi chứng tỏ một đẳng thức tao hoàn toàn có thể đổi khác vế này trở nên vế ê, đổi khác tương tự, đổi khác nhì vế nằm trong vì như thế một đại lượng không giống.

  • Chứng minh biểu thức ko dựa vào góc x.

  •  Hay giản dị và đơn giản biểu thức tao nỗ lực thực hiện xuất hiện tại nhân tử công cộng ở tử và kiểu nhằm rút gọn gàng hoặc thực hiện xuất hiện tại những hạng tử ngược vệt nhằm rút gọn gàng lẫn nhau.

Ví dụ: Chứng minh những đẳng thức sau (giả sử những biểu thức sau đều phải có nghĩa): 

  1. cos^{4}x + 2sin^{2} x = 1 + sin^{4}x

  2. \sqrt{sin^{4}x + 4cos^{2}x} + \sqrt{cos^{4} x+ 4sin^{2}x} = 3tan(x + \frac{\pi}{3}) tan(\frac{\pi}{6} - x)

Cách giải: 

1. Đẳng thức tương tự với cos^{4}x = 1 - 2sin^{2}x + (sin^{2}x)^{2} \Leftrightarrow cos^{4}x = (1 - sin^{2}x)^{2} (*)

Mà sin^{2}x + cos^{2}x = 1 \Rightarrow cos^{2}x = 1 - sin^{2}x

Kết phù hợp với (*) tao hoàn toàn có thể chứng tỏ được 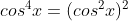cos^{4}x= (cos^{2}x)^{2} (đúng) ĐPCM.

2.  VT = \sqrt{sin^{4}x + 4(1-sin^{2}x)} + \sqrt{cos^{4}x + 4(1-cos^{2}x)}

= \sqrt{(sin^{2})^{2} - 4sin^{2}x + 4} + \sqrt{(cos^{2})^{2} - 4cos^{2}x + 4}

= \sqrt{(sin^{2}x - 2)^{2}} + \sqrt{(cos^{2}x - 2)^{2}} = (2 - sin^{2}x) + (2 - cos^{2}x)

= 4 - (sin^{2}x + cos^{2}x)

Mặt không giống vì như thế (x + \frac{\pi}{3} + \frac{\pi}{6} - x = \frac{\pi}{2} \Rightarrow tan(\frac{\pi}{6} - x) = cot(x + \frac{\pi}{3}) nên:

VP = 3 tan(x + \frac{\pi}{3}) cot(x + \frac{\pi}{3}) = 3 \Rightarrow VT=VP ĐPCM

Xem thêm: Hình Nền OPPO ❤️ Tuyển Tập Ảnh Nền Điện Thoại OPPO - Gấu Đây - Takimart

Đăng ký tức thì và để được những thầy cô tư vấn và xây đắp suốt thời gian ôn thi đua sớm hiệu suất cao, phù phù hợp với bạn dạng thân

Hy vọng qua quýt nội dung bài viết bên trên, chúng ta học viên tiếp tục bổ sung cập nhật tăng nhiều kỹ năng hữu ích với mọi bài xích tập dượt về cung và góc lượng giác. Hãy truy vấn tức thì nền tảng Vuihoc.vn nhằm ĐK thông tin tài khoản và ôn tập dượt nhiều hơn nữa về những dạng bài xích về lượng giác nhé!

BÀI VIẾT NỔI BẬT

So sánh camera iPhone 14 Pro Max và iPhone 13 Pro Max

iPhone 14 Pro Max được nâng cấp đáng kể về chất lượng camera cả phần cứng và phần mềm. Cùng so sánh camera iPhone 14 Pro Max và iPhone 13 Pro Max, hai chiếc máy có chất lượng nhiếp ảnh hàng đầu.

Giải bài tập SGK Sinh học lớp 9 đầy đủ và hay nhất

Giải bài tập SGK Sinh học lớp 9 là tài liệu tổng hợp đầy đủ các kiến thức trọng tâm những bài tập củng cố kiến thức về Sinh học Di Truyền Và Biến Dị, Sinh Vật Và Môi Trường. Để giúp các em nâng cao hiệu quả học tập, tiết kiệm thời gian làm bài, eLib đã tổng hợp các bài tập SGK Sinh học 9 bao gồm phương pháp giải nhanh chóng và hướng dẫn giải rõ ràng cho từng bài tập. Mời các em cùng tham khảo!

Bài tập phương trình hóa học lớp 8

Bài tập phương trình hóa học lớp 8 được biến soạn có đáp án, hy vọng tài liệu giúp ích cho các bạn học sinh củng cố luyện tập biết cách cân bằng phường trình phản ứng.