Những bí quyết lớn chu vi hình tròn để tối ưu không gian

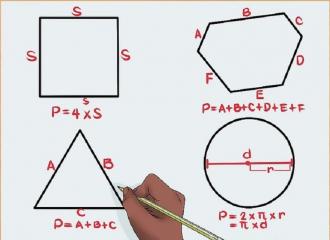
Công thức tính chu vi hình trụ là C = 2πr hoặc C = πd, nhập tê liệt C là chu vi, r là nửa đường kính và d là 2 lần bán kính của hình trụ. Để tính chu vi, tao rất có thể dùng công thức C = 2πr nếu như vẫn biết nửa đường kính, hoặc C = πd nếu như vẫn biết 2 lần bán kính. Trong số đó, π (pi) là một trong độ quý hiếm xấp xỉ khoảng chừng 3.14.

Bạn đang xem: Những bí quyết lớn chu vi hình tròn để tối ưu không gian

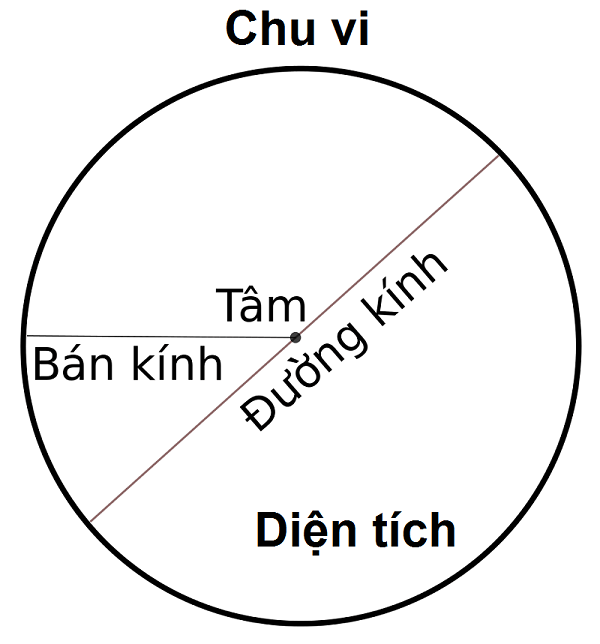
Chu vi hình trụ (hoặc còn được gọi là đàng tròn) là đường giáp ranh biên giới số lượng giới hạn của hình trụ. Để tính chu vi hình trụ, tất cả chúng ta nên biết 2 lần bán kính hoặc nửa đường kính của hình trụ.
Công thức tính chu vi hình trụ là: C = 2πr hoặc C = πd, nhập tê liệt r là nửa đường kính và d là 2 lần bán kính của hình trụ.
Công thức trước tiên là C = 2πr, nhập tê liệt π (pi) có mức giá trị xấp xỉ là 3.14. quý khách rất có thể tính chu vi bằng phương pháp nhân nửa đường kính với 2π.
Công thức loại nhì là C = πd, nhập tê liệt π cũng có thể có độ quý hiếm xấp xỉ là 3.14. quý khách rất có thể tính chu vi bằng phương pháp nhân 2 lần bán kính với π.
Ví dụ, nếu như nửa đường kính hình trụ là 5cm, tao rất có thể tính chu vi bằng phương pháp dùng công thức đầu tiên: C = 2πr = 2π(5) ≈ 2x3.14x5 ≈ 31.4cm.
Tóm lại, chu vi hình trụ là đường giáp ranh biên giới của hình trụ và rất có thể được xem bởi vì công thức C = 2πr hoặc C = πd.

Để tính chu vi hình trụ, tất cả chúng ta rất có thể dùng công thức C = 2πr hoặc C = πd. Tại phía trên, r là nửa đường kính của hình trụ, d là 2 lần bán kính của hình trụ, và π (pi) là một trong hằng số với độ quý hiếm xấp xỉ 3.14.
Bước 1: Xác lăm le nửa đường kính hoặc 2 lần bán kính của hình trụ.
Nếu tao với nửa đường kính của hình trụ, tất cả chúng ta rất có thể tiếp cận bước 2. Nếu ko, nhằm tính nửa đường kính, tao rất có thể dùng công thức r = d/2, nhập tê liệt d là 2 lần bán kính của hình trụ.
Bước 2: kề dụng công thức C = 2πr hoặc C = πd.
Nếu tao biết nửa đường kính của hình trụ, tất cả chúng ta rất có thể tính chu vi bởi vì công thức C = 2πr. Thay thế r bởi vì độ quý hiếm nửa đường kính và triển khai những quy tắc tính.
Nếu tao biết 2 lần bán kính của hình trụ, tất cả chúng ta rất có thể tính chu vi bởi vì công thức C = πd. Thay thế d bởi vì độ quý hiếm 2 lần bán kính và triển khai những quy tắc tính.
Ví dụ: Giả sử tao với cùng 1 hình trụ với nửa đường kính 4 centimet.
- kề dụng công thức C = 2πr:
C = 2 x 3.14 x 4
C ≈ 25.12 cm
Ví dụ khác: Giả sử tao với cùng 1 hình trụ với 2 lần bán kính 10 centimet.
- kề dụng công thức C = πd:
C = 3.14 x 10
C = 31.4 cm
Vì pi là một trong hằng số xấp xỉ, nên sản phẩm đo lường cũng đơn giản xấp xỉ.

Công thức tính chu vi hình trụ là C = 2πr, nhập tê liệt C là chu vi, r là nửa đường kính của hình trụ và π (pi) là một trong hằng số xấp xỉ 3.14159.
Để tính chu vi hình trụ, tao nhân nửa đường kính của hình trụ với 2π. Ví dụ, nếu như nửa đường kính hình trụ là 5 centimet, tao rất có thể tính chu vi bằng phương pháp triển khai quy tắc tính C = 2πr = 2 x 3.14159 x 5 = 31.4159 centimet.
Vậy nếu như biết nửa đường kính của hình trụ, công thức C = 2πr tiếp tục giúp đỡ bạn tính chu vi hình trụ.

Công thức tính chu vi hình trụ là C = 2πr, nhập tê liệt C là chu vi, r là nửa đường kính của hình trụ và π là số pi (tương đối xấp xỉ 3.14). Công thức này được xem bằng phương pháp nhân 2 lần bán kính của hình trụ với số pi hoặc nhân gấp đôi nửa đường kính của hình trụ với số pi.

Chu vi hình trụ với quan hệ với nửa đường kính như sau:
1. Chu vi hình trụ (C) là đường giáp ranh biên giới số lượng giới hạn của hình trụ. Để tính chu vi hình trụ, tao dùng công thức: C = 2 * π * r, nhập tê liệt r là nửa đường kính của hình trụ và π là số Pi (tỷ lệ thân thuộc chu vi và 2 lần bán kính của hình tròn).
2. Mối mối liên hệ thân thuộc chu vi và nửa đường kính của hình trụ rất có thể được hiểu như sau:
- Chu vi của hình trụ với tương quan thẳng cho tới nửa đường kính. Khi nửa đường kính tạo thêm, chu vi cũng tăng theo đuổi và ngược lại, Khi nửa đường kính sụt giảm, chu vi cũng sụt giảm.
- Quan hệ này được thể hiện nay qua quýt công thức C = 2 * π * r. Ta rất có thể thấy rằng nửa đường kính là bộ phận ra quyết định chừng lâu năm chu vi của hình trụ, cùng theo với hằng số π.
Tóm lại, chu vi hình trụ tỉ lệ thành phần thuận với nửa đường kính của hình trụ. Khi nửa đường kính tạo thêm, chu vi cũng tăng theo đuổi theo công thức C = 2 * π * r và ngược lại. Qua tê liệt, quan hệ thân thuộc chu vi và nửa đường kính của hình trụ được thể hiện nay rõ rệt qua quýt công thức tính chu vi hình trụ.

Không, không tồn tại cơ hội này không giống nhằm tính chu vi hình trụ. Chu vi hình trụ chỉ rất có thể được xem bởi vì công thức 2πr (hay πd) với r là nửa đường kính và d là 2 lần bán kính của hình trụ. Đây là công thức cơ phiên bản và có một không hai nhằm tính chu vi hình trụ.

Chu vi hình trụ (hay còn được gọi là đàng tròn) là đường giáp ranh biên giới số lượng giới hạn của hình trụ. Khi tao đo lường chu vi hình trụ, có tương đối nhiều phần mềm nhập cuộc sống đời thường từng ngày. Dưới đó là một vài ví dụ:
1. Xây dựng và loài kiến trúc: Khi design một vòng tròn trặn, như bánh xe pháo xe hơi hoặc đĩa tách, rất cần được đo lường chu vi hình trụ để hiểu độ dài rộng và tỷ trọng tương thích nhằm thành phầm hoạt động và sinh hoạt một cơ hội hiệu suất cao.
2. Định giá bán bất tỉnh sản: Khi Review độ quý hiếm của một miếng khu đất với hình dạng gần như là hình trụ, chu vi hình trụ được dùng Như một nhân tố cần thiết nhằm đo lường diện tích S và xác lập độ quý hiếm của khu đất nền.
3. Tính chi phí gửi ngân hàng: Trong một vài tình huống, ngân hàng dùng chu vi hình trụ nhằm tính lãi vay trong các công việc tính lãi kép (compound interest) mang đến việc gửi tiết kiệm chi phí tự động hóa.
4. Hình tròn trặn nhập thể dục: Chu vi hình trụ được dùng nhằm đo lường chừng lâu năm của những vòng tròn trặn nhập một vài bài bác tập luyện thể thao như động đậy tròn trặn (circular motion) hoặc quy trình của một vật.
5. Trò nghịch ngợm và thể thao: Trong bi-a, bowling và nhiều trò nghịch ngợm không giống, chu vi hình trụ được dùng nhằm tính điểm và xác lập độ dài rộng và địa điểm của những đối tượng người dùng.
Tổng hợp ý lại, chu vi hình trụ với phần mềm rộng lớn nhập cuộc sống đời thường từng ngày, kể từ design thi công, lăm le giá đất nền đai, tài chủ yếu ngân hàng, thể thao, cho tới trò nghịch ngợm và thể thao.

Để tính diện tích S hình trụ Khi chỉ biết chu vi, tao rất có thể dùng công thức sau:
S = (C²)/(4π)
Trong đó:
- S là diện tích S hình tròn
- C là chu vi hình tròn
- π là số Pi, có mức giá trị xấp xỉ 3.14
Ví dụ, fake sử tao biết chu vi của hình trụ là 10 đơn vị chức năng, tao tiếp tục thay cho độ quý hiếm chu vi nhập công thức:
S = (10²)/(4π)
S = 100/(4 x 3.14)
S = 25.32 đơn vị chức năng vuông
Vậy, lúc biết chu vi của hình trụ là 10 đơn vị chức năng, diện tích S của hình trụ là khoảng chừng 25.32 đơn vị chức năng vuông.

Công thức tính diện tích S hình trụ dựa vào chu vi là:
1. Tính nửa đường kính của hình trụ bằng phương pháp lấy chu vi (C) phân chia mang đến 2π (với π là số Pi, có mức giá trị xấp xỉ là 3.14159).
r = C / (2π)
2. Tính diện tích S hình trụ bằng phương pháp nhân nửa đường kính (r) với chủ yếu nó và với π.
S = π * r^2
Ví dụ: Nếu chu vi của hình trụ là 10, tao rất có thể tính nửa đường kính bởi vì cách:
r = 10 / (2 * 3.14159) ≈ 1.59155
Sau tê liệt, tao rất có thể tính diện tích S của hình trụ bởi vì cách:
S = 3.14159 * (1.59155)^2 ≈ 7.95773
Vậy diện tích S của hình trụ là khoảng chừng 7.95773.

Diện tích hình trụ với quan hệ với nửa đường kính và chu vi như sau:
1. Bán kính (r) của hình trụ là chừng lâu năm kể từ trung điểm của hình trụ cho tới ngẫu nhiên điểm này bên trên đàng viền của chính nó. Bán kính được ký hiệu là r.
2. Chu vi (C) của hình trụ là chừng lâu năm của đàng viền của hình trụ. Chu vi được ký hiệu là C.
3. Công thức tính chu vi (C) của hình trụ là: C = 2πr, nhập tê liệt π (pi) là một trong hằng số xấp xỉ 3.14159.
4. Công thức tính diện tích S (A) của hình trụ là: A = πr^2.
5. Ta rất có thể thấy rằng chu vi (C) và nửa đường kính (r) với quan hệ hình học tập trải qua hằng số π. Chu vi là lươn lượng đo đàng viền của hình trụ, trong những khi nửa đường kính là lươn lượng đo kể từ trung điểm của hình trụ cho tới ngẫu nhiên điểm này bên trên đàng viền.
6. Diện tích (A) là lươn lượng đo không giống, nó đo diện tích S của hình trụ, và nó được xem bằng phương pháp nhân nửa đường kính (r) với chủ yếu nó và nhân với π.
Tóm lại, chu vi và diện tích S của hình trụ với quan hệ với nửa đường kính trải qua công thức đo lường, nhập tê liệt hằng số π nhập vai trò cần thiết.

Diện tích và chu vi hình trụ có tương đối nhiều phần mềm nhập thực tiễn, bao gồm:
1. Xây dựng và loài kiến trúc: Khi đo lường diện tích S hình trụ, tất cả chúng ta rất có thể dùng nhằm mò mẫm độ dài rộng và diện tích S của những đối tượng người dùng tròn trặn như hồ nước tập bơi, vòng tròn trặn thao tác, sảnh đá bóng mini, hoặc đàng tròn trặn nhập nghệ thuật thi công và bản vẽ xây dựng.
2. Ngành công nghiệp: Chu vi và diện tích S hình trụ được dùng nhập ngành công nghiệp tạo ra và gia công. Ví dụ, Khi gia công những cụ thể với hình dạng tròn trặn như ống, tế bào tơ, đĩa tách, chén bát tròn trặn, việc đo lường chu vi và diện tích S sẽ hỗ trợ xác lập độ dài rộng và thông số kỹ thuật nghệ thuật quan trọng.
3. Giáo dục: Tính toán chu vi và diện tích S hình trụ là những kỹ năng cơ phiên bản nhập dạy dỗ toán học tập cấp cho đái học tập và trung học tập hạ tầng. Nó gom những học viên hiểu về định nghĩa đàng tròn trặn, nửa đường kính, 2 lần bán kính, mò mẫm hiểu địa thế căn cứ mang đến công thức tính chu vi và diện tích S, và vận dụng nhập giải những bài bác tập luyện thực tiễn.
4. Địa lí và khối hệ thống phiên bản đồ: Chu vi hình trụ được dùng nhằm đo lường chừng lâu năm đàng viền của một điểm hình trụ bên trên phiên bản vật dụng. Như vậy cần thiết trong các công việc xác lập vùng tròn trặn, nửa đường kính, và địa điểm của những đối tượng người dùng địa lý, như hồ nước, vườn vương quốc hoặc đàng tròn trặn nhập khối hệ thống giao thông vận tải.
5. Công nghệ và năng lượng điện tử: Chu vi hình trụ cũng rất được dùng trong những phần mềm technology và năng lượng điện tử, như nhập design vòng cảm và vòng tụ, hoặc trong các công việc đo lường tỉ lệ thành phần không ngừng mở rộng của những đĩa năng lượng điện tử.
Tóm lại, diện tích S và chu vi hình trụ có tương đối nhiều phần mềm thực tiễn trong vô số nghành nghề dịch vụ như thi công, công nghiệp, dạy dỗ, địa lý, technology và năng lượng điện tử.

Để tính được nửa đường kính của hình trụ lúc biết chu vi, tất cả chúng ta rất có thể vận dụng công thức: nửa đường kính = chu vi / 2π.
Bước 1: Xác định vị trị chu vi của hình trụ.
- Trong tình huống này, fake sử chu vi của hình trụ là C.
Bước 2: kề dụng công thức tính nửa đường kính.
- Sử dụng công thức nửa đường kính = chu vi / 2π, tao thay cho thế độ quý hiếm chu vi C nhập công thức và đo lường.
Ví dụ:
Nếu chu vi của hình trụ là đôi mươi centimet, tao triển khai quá trình như sau:
- Bán kính = đôi mươi / (2 x π) = đôi mươi / (2 x 3.14) ≈ 3.18 centimet.
Vậy, nếu như biết độ quý hiếm chu vi của hình trụ, tao rất có thể tính được nửa đường kính bằng phương pháp phân chia chu vi mang đến 2π.

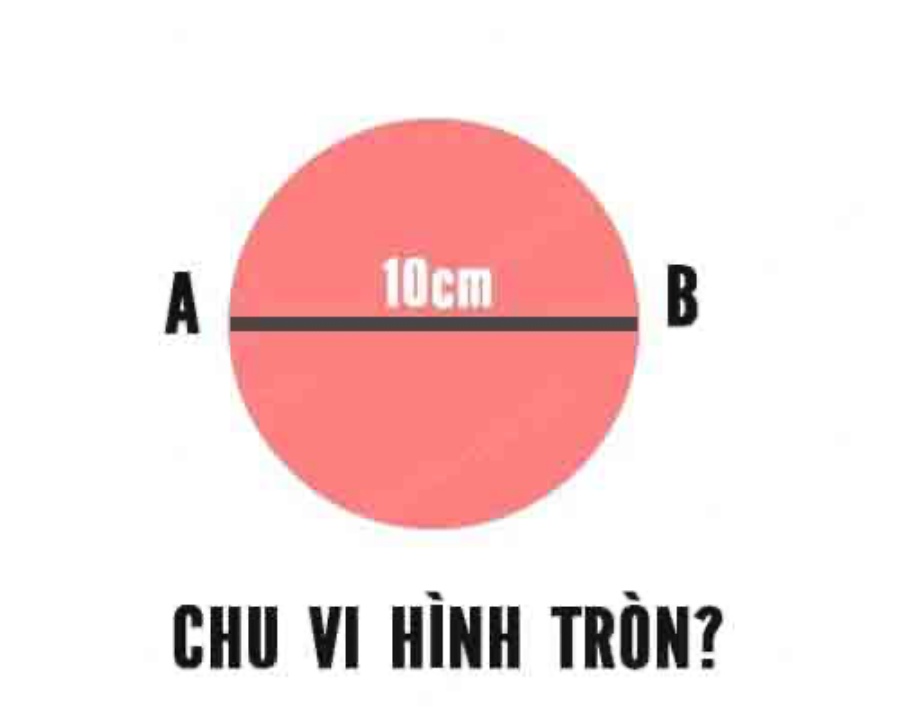
Công thức tính nửa đường kính dựa vào chu vi của hình trụ là r = C / (2 * π), nhập tê liệt r là nửa đường kính của hình trụ, C là chu vi của hình trụ và π (gọi là pi) là một trong hằng số xấp xỉ bởi vì 3.14. Để tính nửa đường kính, tao phân chia chu vi của hình trụ mang đến nhì chuyến độ quý hiếm của π.
Ví dụ, nếu như tao với cùng 1 hình trụ với chu vi là 10cm, tao rất có thể tính nửa đường kính như sau:
r = C / (2 * π)
r = 10cm / (2 * 3.14)
r ≈ 1.59cm
Vậy nửa đường kính của hình trụ nhập ví dụ bên trên là khoảng chừng 1.59cm.

Tính toán chu vi, diện tích S và nửa đường kính của hình trụ là những định nghĩa cơ phiên bản nhập hình học tập và ý nghĩa cần thiết trong vô số nghành nghề dịch vụ không giống nhau. Dưới đó là những nguyên nhân về tại vì sao đo lường này quan liêu trọng:
1. Ứng dụng nhập hình học: Chu vi, diện tích S và nửa đường kính của hình trụ là những thông số kỹ thuật cơ phiên bản nhập hình học tập. Chúng gom tất cả chúng ta hiểu và phân tách những tính chất của hình trụ, cũng giống như các hình không giống tương quan như hình cầu, vòng tròn trặn và đàng tròn trặn.
2. Ứng dụng nhập ngẫu nhiên và khoa học: Hình tròn trặn được dùng rộng thoải mái trong những nghành nghề dịch vụ không giống nhau như nghệ thuật, cơ vật lý và toán học tập. Việc đo lường chu vi, diện tích S và nửa đường kính của hình trụ gom tất cả chúng ta giải quyết và xử lý nhiều yếu tố thực tiễn nhập cuộc sống đời thường từng ngày và phân tích khoa học tập.
3. Ứng dụng nhập đo lường: Chu vi, diện tích S và nửa đường kính của hình trụ được dùng trong những Việc giám sát. Ví dụ, đo lường chu vi của một hình trụ rất có thể gom tất cả chúng ta xác lập chiều lâu năm một hình trụ được vẽ bên trên mặt mũi khu đất nhập việc làm giám sát hoặc thi công.
4. Ứng dụng nhập design và xây dựng: Khi design và thi công những dự án công trình, việc đo lường chu vi, diện tích S và nửa đường kính của hình trụ là quan trọng. Đây là những thông số kỹ thuật cần thiết nhằm đo lường lượng vật tư quan trọng, đánh giá hình dạng và độ dài rộng của những bộ phận nhập dự án công trình.
5. Ứng dụng nhập dạy dỗ và phía dẫn: Tính toán chu vi, diện tích S và nửa đường kính của hình trụ là nội dung cơ phiên bản nhập công tác dạy dỗ và huấn luyện. Việc hiểu và vận dụng những định nghĩa này gom cách tân và phát triển khả năng suy nghĩ logic và xử lý vấn đề mang đến học viên và SV.
Tóm lại, đo lường chu vi, diện tích S và nửa đường kính của hình trụ không những ý nghĩa cơ phiên bản nhập hình học tập tuy nhiên còn tồn tại phần mềm rộng thoải mái trong vô số nghành nghề dịch vụ không giống nhau. Việc hiểu và vận dụng bọn chúng gom tất cả chúng ta vận dụng kỹ năng và giải quyết và xử lý những yếu tố thực tiễn một cơ hội hiệu suất cao.

Xem thêm: Hình Nền OPPO ❤️ Tuyển Tập Ảnh Nền Điện Thoại OPPO - Gấu Đây - Takimart