Diện tích hình thang vuông là 1 phần kiến thức và kỹ năng cần thiết vô toán hình học tập. Để canh ty những em dễ dàng và đơn giản ghi lưu giữ công thức, tóm được phương pháp tính và giải bài xích luyện hiệu suất cao thì nội dung tại đây Monkey tiếp tục phân tách cụ thể.
Hình thang vuông là gì?
Hình thang vuông là một trong dạng đặc biệt quan trọng của hình thang khi mang trong mình 1 góc vuông.
Dấu hiệu nhận thấy hình thang vuông khá đơn giản và giản dị đó là hình thang mang trong mình 1 góc vuông. Đồng thời, cạnh góc vuông này cũng đó là độ cao của hình.
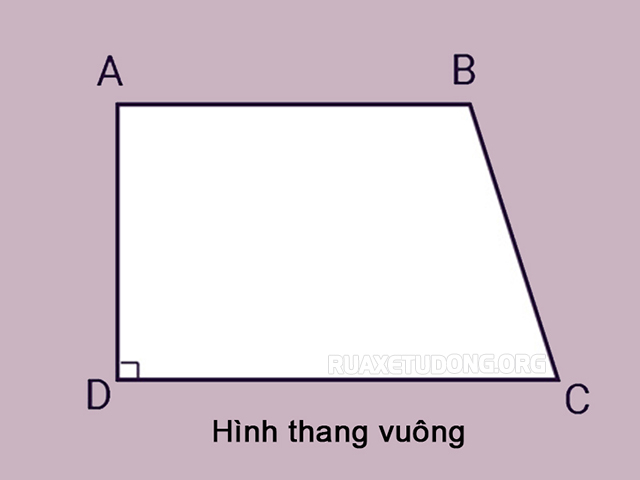
Công thức tính diện tích hình thang vuông
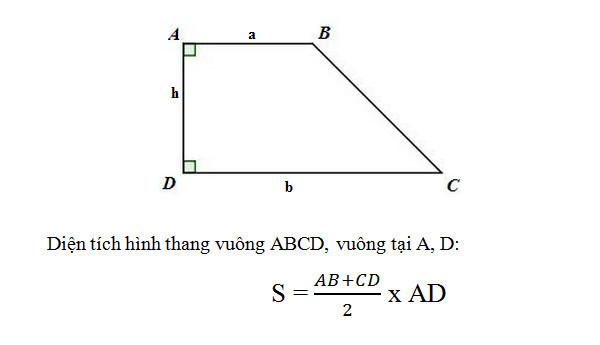
Trong toán học tập, diện tích của hình thang vuông sẽ tiến hành tính vì thế một nửa tích của tổng 2 lòng và độ cao ứng với 2 cạnh lòng. Hoặc diện tích S hình thang vuông vì thế tích của đàng cao và khoảng nằm trong của 2 đáy
S = 1⁄2 h (a + b)
Trong đó:
-
S: Diện tích hình thang
-
a, b: Độ lâu năm 2 lòng của hình thang
-
h: Độ lâu năm đàng cao (chính là cạnh vuông góc với 2 cạnh đáy)
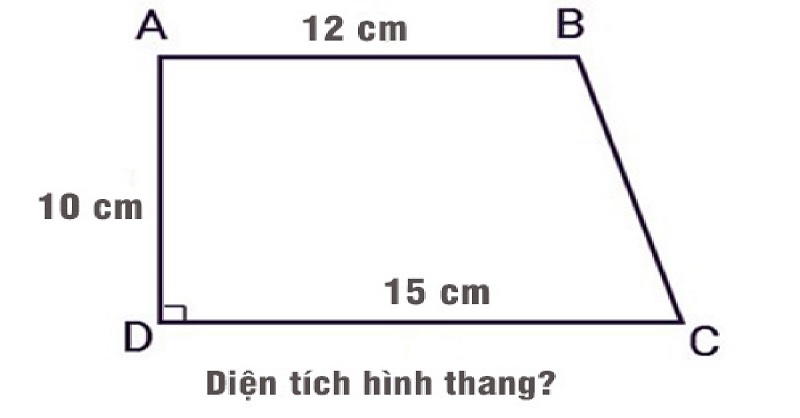
Ví dụ: Cho hình thang ABCD vuông bên trên D với cạnh AD lâu năm 10 centimet, AB lâu năm 12 centimet, DC lâu năm 15 centimet. Tính diện tích S hình thang.
Lời giải:
Theo đề bài xích tao có:
AB = 12 cm
AD = 10 cm
DC = 15 centimet. Đây là cạnh mặt mũi, cạnh góc vuông bên cạnh đó là độ cao của hình thang.
Áp dụng công thức tính diện tích hình thang vuông, tao có:
S = 1⁄2 h (a + b) = 1⁄2 x AD x (AB+DC) = 1⁄2 x 10 x (12+15) = 135 cm2
Đáp số: 135 cm2
Mẹo ghi lưu giữ công thức tính diện tích hình thang vuông
Để canh ty những em dễ dàng và đơn giản ghi lưu giữ công thức tính diện tích S của hình thang vuông, bên dưới đấy là một vài ba mẹo nhằm quý khách tham lam khảo:
-
Nắm rõ rệt quy tắc cơ bản: Diện tích của hình thang vuông đó là vì thế 1/2 tích của tổng 2 lòng và độ cao ứng với 2 cạnh lòng hoặc tích phỏng lâu năm lòng rộng lớn và độ cao phân tách song. Nên việc ghi lưu giữ công thức là vấn đề cần thiết.
-
Hình dung rời khỏi hình thang vuông: Đây là hình thang nên có một cạnh góc vuông tê liệt đó là độ cao, nằm trong nhị lòng tuy nhiên song và nhị cạnh đối lập cân nhau.
-
Biểu biểu diễn công thức vô hình ảnh: Các em rất có thể vẽ một hình tam giác bên phía trong hình thang vì thế độ cao và một lòng. Như vậy tiếp tục giúp cho bạn thấy rõ nét cơ hội công thức hoạt động và sinh hoạt.
-
Lưu ý với đơn vị chức năng đo: Khi giải bài xích thói quen diện tích S của hình thang vuông, cần thiết đáp ứng những cạnh nên đem nằm trong đơn vị chức năng đo. Chẳng hạn độ cao đo vì thế centimet thì lòng cũng nên là centimet nhằm đo lường đúng mực.
-
Thực hành nhiều bài xích tập: Hãy dò thám nhiều bài xích luyện tương quan cho tới tính diện tích hình thang vuông và thực hành thực tế bọn chúng. Như vậy sẽ hỗ trợ những em dễ dàng và đơn giản thích nghi và ghi lưu giữ công thức và nâng cấp kĩ năng đo lường.
-
Ứng dụng toán vô thực tiễn: Các em rất có thể links công thức với ví dụ thực tiễn giúp thấy rõ rệt phần mềm của chính nó. Chẳng hạn: Tính diện tích S một mảnh đất nền, tấm gạch… hình thang vuông vô việc làm kiến tạo hoặc trong nghành nghề design hình họa.
-
Mẹo ghi lưu giữ công thức tính diện tích hình thang vuông qua chuyện bài xích thơ:
Muốn tính diện tích S hình thang
Đáy rộng lớn lòng nhỏ tao đem nằm trong vào
Cộng vô nhân với chiều cao
Chia song lấy nửa thế nào thì cũng rời khỏi.
GIÚP CON HỌC TOÁN KẾT HỢP VỚI TIẾNG ANH SIÊU TIẾT KIỆM CHỈ TRÊN MỘT APP MONKEY MATH. VỚI NỘI DUNG DẠY HỌC ĐA PHƯƠNG PHÁP GIÚP BÉ PHÁT TRIỂN TƯ DUY NÃO BỘ VÀ NGÔN NGỮ TOÀN DIỆN CHỈ VỚI KHOẢNG 2K/NGÀY.
Các dạng bài xích luyện tương quan cho tới tính diện tích hình thang vuông
Trong công tác toán học tập, những em sẽ tiến hành thích nghi và nên đoạt được với một vài dạng bài xích luyện về tính chất diện tích S của hình thang vuông như sau:
Dạng 1: Tính diện tích S hình bình thang vuông lúc biết phỏng lâu năm nhị lòng và chiều cao
Phương pháp giải: sít dụng tức thì công thức tính diện tích S của hình thang vuông tê liệt nhằm đo lường đúng mực.
Ví dụ: Cho hình thang biết phỏng lâu năm lòng nhỏ vì thế 5cm, lòng rộng lớn vì thế 10cm. Chiều cao là 6cm. Tính diện tích S của hình thang tê liệt.
Lời giải:
Diện tích hình thang là:
(5 + 10) x 6 : 2 = 45 (cm2)
Đáp số: 45cm2
Dạng 2: Tính độ cao lúc biết phỏng lâu năm nhị lòng và ăn mặc tích
Phương pháp giải: Từ công thức tính diện tích S, tao suy rời khỏi được công thức tính độ cao ứng của hình thang vuông được xem là lấy diện tích S phân tách mang đến khoảng nằm trong của nhị lòng hoặc h = S x 2 : (a + b).
Ví dụ: Cho hình thang vuông, biết diện tích S là 14dm2, lòng nhỏ nhắn là 2dm và lòng rộng lớn là 5dm. Tính phỏng lâu năm độ cao của hình thang vuông tê liệt.
Lời giải:
Độ lâu năm độ cao của hình thang là:
14 x 2 : (2 + 5) = 4 (dm)
Đáp số: 4dm
Dạng 3: Tính diện tích S hình thang vuông khi chưa chắc chắn phỏng lâu năm nhị lòng và chiều cao
Phương pháp giải: Ta tiếp tục phụ thuộc vào đề bài xích thể hiện vấn đề về độ cao hoặc phỏng lâu năm nhị lòng. Từ này sẽ nên dò thám phỏng lâu năm của cạnh còn sót lại nhằm tình diện tích S của hình.
Ví dụ: Cho hình thang vuông, biết độ cao là 56cm. Đáy to hơn lòng nhỏ nhắn 24cm và lòng nhỏ nhắn vì thế 2/5 lòng rộng lớn. Tính diện tích S hình thang.
Lời giải:
Hiệu số phần cân nhau là:
5 – 2 = 3 (phần)
Xem thêm: Chu vi xích đạo của trái đất
Độ lâu năm lòng rộng lớn là:
24 : 3 x 5 = 40 (cm)
Độ lâu năm lòng nhỏ nhắn là:
40 – 24 = 16 (cm)
Diện tích hình thang là:
(16 + 40) x 56 : 2 = 1568 (cm2)
Đáp số: 1568cm2
Bài luyện tính diện tích hình thang vuông luyện tập
Để nắm rõ rộng lớn về kiểu cách tính diện tích S của hình thang vuông, bên dưới đấy là một vài bài xích luyện nhưng mà những em rất có thể tìm hiểu thêm và thực hành thực tế.
Bài luyện đem điều giải
Bài luyện 1: Tính diện tích S hình thang biết phỏng lâu năm nhị lòng theo thứ tự là 18cm và 14cm; độ cao là 9cm
Giải:
Áp dụng công thức tính diện tích S hình thang tao có:
S = ((18 +14) x 9)/2 = 144 (cm2)
Đáp số: 144 cm2
Bài luyện 2: Có một mảnh đất nền hình thang với lòng nhỏ nhắn là 24m, lòng rộng lớn là 30m. Mở rộng lớn nhị dáy về phía phía bên phải của mảnh đất nền với lòng rộng lớn tăng 7m, lòng nhỏ tăng 5m nhận được mảnh đất nền hình thang mới mẻ với diện tích S to hơn diện tích S thuở đầu là 36m2. Tính diện tích S mảnh đất nền hình thang thuở đầu.
Giải:
Theo đầu bài xích, diện tích S gia tăng là diện tích S hình thang đem lòng rộng lớn là 7m và lòng nhỏ là 5m. Do tê liệt, độ cao mảnh đất nền hình thang là: h = (36 x 2) : (7 + 5) = 6m
Diện tích mảnh đất nền thuở đầu là: S = 6 . (24 + 30) : 2 = 162m²
Bài luyện 3:
Cho hình thang vuông đem khoảng cách 2 lòng là 16cm, lòng nhỏ vì thế ¾ lòng rộng lớn. Tính phỏng lâu năm 2 lòng lúc biết được diện tích S hình thang vuông là 112cm².
Giải:
Khoảng cơ hội 2 lòng vô hình thang vuông đó là độ cao hình thang nên:
Tổng phỏng lâu năm nhị lòng là (112 x 2) : 16 = 14cm
Ta gọi phỏng lâu năm lòng nhỏ nhắn là a, phỏng lâu năm lòng rộng lớn là b, tao có:
a + b = 14 và a = ¾ b
Nên a = 14 x 4: 7 = 8cm
Do tê liệt, lòng nhỏ nhắn = 34/7 centimet, lòng rộng lớn 64/7 cm
Bài luyện 4: Cho hình thang vuông đem khoảng cách nhị lòng là 96 centimet và lòng nhỏ vì thế 4/7 lòng rộng lớn. Tính phỏng lâu năm nhị lòng, biết diện tích S hình thang là 6864 cm2
Giải:
Khoảng cơ hội nhị lòng đó là độ cao của hình thang tê liệt suy rời khỏi h = 96 cm
Tổng phỏng lâu năm nhị lòng là
(6864×2) / 96 = 143 cm
Độ lâu năm lòng nhỏ nhắn là
143 / (4 + 7) x 4 = 52 cm
Dộ lâu năm lòng rộng lớn là
143 – 52 = 91 cm
Bài luyện 5: Tính diện tích S mảnh đất nền hình thang ABCD vuông bên trên A, biết AB = 10 centimet, CD = 12 centimet và AD = 6 cm
Giải:
Áp dụng công thức tính diện tích hình thang vuông tao có
SABCD = (a + b). h/2 = (AB + CD). AD/2 = (10 + 12). 6/2 = 66 cm2
Bài luyện tự động luyện
Bài luyện 1: Hình bình thang vuông đem lòng rộng lớn 10 centimet, lòng nhỏ 6 centimet và độ cao 8 centimet. Hãy tính diện tích S của chính nó.
Bài luyện 2: Bạn mang trong mình 1 hình bình thang vuông với lòng rộng lớn 15 centimet, lòng nhỏ 9 centimet và độ cao 12 centimet. Tính diện tích S của hình này.
Bài luyện 3: Hãy tính diện tích S của một hình bình thang vuông đem lòng rộng lớn 18 centimet, lòng nhỏ 12 centimet và độ cao 10 centimet.
Bài luyện 4: Bạn mang trong mình 1 hình bình thang vuông với lòng rộng lớn 14 centimet, lòng nhỏ 8 centimet và diện tích S 56 cm². Tính độ cao của hình này.
Bài luyện 5: Tính diện tích S của hình bình thang vuông đem lòng rộng lớn đôi mươi centimet, lòng nhỏ 16 centimet và độ cao 7 centimet.
Bài luyện 6: Hãy tính diện tích S của một hình bình thang vuông đem lòng rộng lớn 25 centimet, lòng nhỏ 15 centimet và độ cao 9 centimet.
Bài luyện 7: Quý Khách mang trong mình 1 hình bình thang vuông với lòng rộng lớn 30 centimet, lòng nhỏ đôi mươi centimet và độ cao 12 centimet. Tính diện tích S của chính nó.
Bài luyện 8: Tính diện tích S của hình bình thang vuông đem lòng rộng lớn 16 centimet, lòng nhỏ 10 centimet và độ cao 5 centimet.
Bài luyện 9: Hãy tính diện tích S của một hình bình thang vuông đem lòng rộng lớn 28 centimet, lòng nhỏ 18 centimet và độ cao 8 centimet.
Bài luyện 10: Quý Khách mang trong mình 1 hình bình thang vuông với lòng rộng lớn 40 centimet, lòng nhỏ 24 centimet và diện tích S 168 cm². Tính độ cao của chính nó.
Bài luyện 11: Tính diện tích S hình thang vuông đem độ cao vì thế 4 dm, lòng nhỏ nhắn vì thế 80% độ cao và tầm thường lòng rộng lớn 1,2 dm.
Xem thêm: Công thức tính Diện tích hình vuông, hình chữ nhật, hình tròn, hình tam giác...
Bài luyện 12: Hình thang đem lòng to hơn lòng nhỏ nhắn đôi mươi,4 dm và vì thế 5/3 lòng nhỏ nhắn, độ cao rộng lớn lòng nhỏ nhắn 2,1 dm. Tính diện tích S hình thang.
Bài luyện 13: Hình thang vuông đem tổng phỏng lâu năm nhị lòng vì thế 14,5 dm, lòng rộng lớn cuống quýt rưỡi lòng nhỏ nhắn, độ cao tầm thường lòng nhỏ nhắn 2,8 dm. Tính diện tích S hình thang.
Kết luận
Trên đấy là tổ hợp những kiến thức và kỹ năng về cách tính diện tích hình thang vuông. Hy vọng phụ thuộc vào những share bên trên sẽ hỗ trợ những em dễ dàng và đơn giản thâu tóm, ghi lưu giữ và thỏa sức tự tin đoạt được những bài xích luyện tương quan hiệu suất cao nhất.
Bình luận