Bí quyết tính chu vi tam giác: Đều, Cân, Vuông

Hướng dẫn cụ thể phương pháp tính chu vi tam giác thông thường, tam giác đều, tam giác cân nặng. Kiến thức này giúp cho bạn xử lý nhanh gọn lẹ bài bác luyện học tập và vận dụng linh động nhập việc làm hao hao cuộc sống đời thường hằng ngày.

Lợi ích của việc tính chu vi tam giác:

Bạn đang xem: Bí quyết tính chu vi tam giác: Đều, Cân, Vuông

+ Nắm vững vàng công thức toán nhập lịch trình học

+ sát dụng nhập thực tiễn việc làm và cuộc sống đời thường hằng ngày nhằm tính chu vi những vật thể tam giác.

Đặc điểm của tam giác: Hình khối được dẫn đến kể từ 3 điểm ko trực tiếp sản phẩm, với phụ thân cạnh là những đoạn trực tiếp nối những điểm tê liệt cùng nhau.

Khái niệm và Công thức Tính Chu Vi Tam Giác

Tam giác được phân loại trở thành 4 dạng chính: tam giác thông thường, tam giác vuông, tam giác cân nặng, tam giác vuông cân nặng và tam giác đều, nhờ vào đặc điểm của góc và cạnh nhập tam giác.

Trong nội dung bài viết này, Mytour.vn tiếp tục chỉ dẫn phương pháp tính chu vi mang đến từng loại tam giác, giúp cho bạn vận dụng linh động nhập giải bài bác luyện và tính chu vi của tam giác nhập thực tiễn.

Cách Tính Chu Vi Tam Giác

1. Chu Vi Tam Giác Thường

Công thức tính chu vi tam giác thường: Phường = a + b + c, với a, b, c là phỏng nhiều năm phụ thân cạnh của tam giác.

Công Thức Chu Vi Tam Giác Thường

Chu vi tam giác Phường vì chưng tổng phỏng nhiều năm phụ thân cạnh a, b, c của tam giác.

Tính nửa chu vi tam giác: 1/2 Phường = (a + b + c)/2

Hình minh họa và Cách tính chu vi tam giác thông thường.

Ví dụ 1: Tính chu vi tam giác hình 2D

Tính chu vi tam giác kể từ Độ Dài Cạnh

Lời Giải: Sử dụng công thức tính chu vi tam giác: Phường = a + b + c.

Với tài liệu bài bác toán: a = 3 centimet, b = 4 centimet, c = 5 centimet.

Chu vi của tam giác được xem vì chưng cách: Phường = 3 + 4 + 5 = 12 centimet.

Ví dụ 2: Tính Chu Vi Tam Giác thạo 3 Cạnh

Cho tam giác với 2 cạnh mặt mày là 3 centimet và 4 centimet, cạnh sót lại gấp hai tổng phỏng nhiều năm nhị cạnh tê liệt. Hãy tính chu vi tam giác tê liệt.

Bài Giải Cho Tam Giác ABC

Gọi tam giác cần thiết tính chu vi là ABC

Theo câu hỏi, tao biết: AB = 3cm, AC = 4 centimet và BC = 2 (AB + AC)

Chiều nhiều năm cạnh sót lại của tam giác là: BC = 2 (AB + AC) = 14 cm

Chu vi tam giác ABC thời điểm hiện nay là: Phường (ABC) = AB + AC + BC = 3 + 4 + 14 = 21 cm

2. Cách tính chu vi tam giác vuông

Khái Niệm về Tam Giác Vuông

- Chu vi tam giác vuông được xem bám theo công thức: Phường = a + b + c

Trong đó:

+ Hai cạnh a và b của tam giác vuông

Xem thêm: Chu vi xích đạo của trái đất

+ c là cạnh huyền của tam giác vuông.

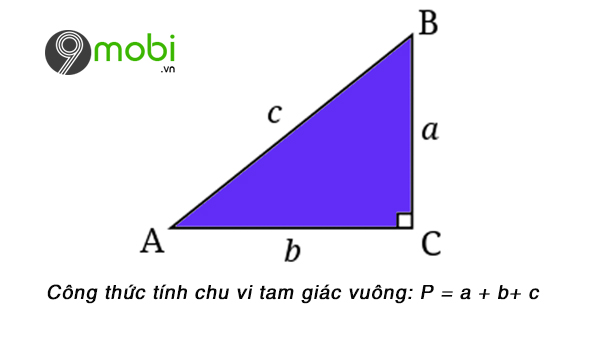
Hình hình ảnh tam giác vuông và phương pháp tính chu vi tam giác vuông.

Ví dụ 3: Tính Chu Vi Tam Giác

Cho tam giác cân nặng ABC với những cạnh có tính nhiều năm là 8 centimet, 10 centimet và 12 centimet. Hãy tính chu vi của tam giác này.

Bài Giải: Dựa nhập công thức tính chu vi tam giác, tao có

- Chu vi tam giác cân nặng ABC là: Phường (ABC) = 8 + 10 + 12 = 30cm

3. Cách tính chu vi tam giác cân

Khái Niệm: Tam giác cân nặng là tam giác đem 2 cạnh mặt mày đều nhau.

- Chu Vi Tam Giác Cân: Phường = 2a + c

Trong tê liệt a : Hai cạnh mặt mày của tam giác, c là lòng của tam giác.

Công thức tính chu vi này cũng vận dụng mang đến tam giác vuông cân nặng (tam giác có một góc vuông và 2 cạnh mặt mày vì chưng nhau)

Hình hình ảnh minh họa tam giác cân nặng, phương pháp tính chu vi tam giác cân nặng.

Ví dụ 4: Tính chu vi tam giác cân nặng ABC khi chiều nhiều năm cạnh mặt mày là 5 centimet, chiều nhiều năm cạnh lòng là 8cm

Lời giải:

Vì tam giác ABC là tam giác đều nên tao có: AC = AB = 5cm

Áp dụng công thức tính chu vi tam giác đều, tao có

- Chu vi tam giác ABC là: Phường (ABC) = 3 x 5 = 15 cm

4. Cách tính chu vi tam giác đều

Khái niệm: Tam giác đều là tam giác đem 3 cạnh vì chưng nhau

- Công thức tính chu vi tam giác đều: Phường = 3 x a

Trong công thức: Phường là chu vi tam giác đều, a là chiều nhiều năm cạnh của tam giác

Hình hình ảnh minh họa tam giác đều và phương pháp tính chu vi.

Ví dụ 5: Tính chu vi tam giác đều ABC với chiều nhiều năm cạnh AB = 5 cm

Lời giải:

Vì tam giác ABC là tam giác đều nên tao đem, phỏng nhiều năm những cạnh là: AB = AC = BC = 5cm

Dựa nhập công thức tính chu vi tam giác đều, tao có: Phường (ABC) = 5 x 3 = 15cm

Xem thêm: Lý thuyết Đường thẳng vuông góc với mặt phẳng - Toán 11 Cánh diều | SGK Toán 11 - Cánh diều

Hiểu biết về diện tích S và chu vi tam giác là kỹ năng cần thiết tuy nhiên học viên cần thiết nắm rõ khi ngồi bên trên ghế căn nhà ngôi trường. Không chỉ chung xử lý những câu hỏi kể từ dễ dàng cho tới khó khăn mà còn phải tương hỗ ý hợp tâm đầu nhập cuộc sống đời thường và việc làm trong tương lai.

https://Mytour.vn/cach-tinh-chu-vi-tam-giac-25727n.aspx
Cùng với tam giác, việc tính chu vi hình chữ nhật cũng lôi cuốn sự quan hoài của rất nhiều người nhập quy trình học tập và thao tác. Nếu bạn thích tính chu vi và diện tích S hình chữ nhật tuy nhiên ko lưu giữ công thức, nội dung bài viết chỉ dẫn phương pháp tính chu vi hình chữ nhật kể từ Mytour.vn tiếp tục giúp cho bạn trả lời từng vướng mắc.