Cách xác định góc giữa đường thẳng và mặt phẳng dễ hiểu nhất - IMO2007

Hiểu được góc thân ái đường thẳng liền mạch và mặt mũi phẳng lì là một trong kỹ năng và kiến thức cơ bạn dạng cần thiết lúc học toán. Nắm vững vàng định nghĩa này sẽ hỗ trợ những em tiến bộ xa xôi rộng lớn trong công việc xử lý những bài bác tập luyện và câu hỏi tương quan. Tuy nhiên, việc xác lập góc thân ái bọn chúng ko cần khi nào thì cũng đơn giản và dễ dàng.

Bạn đang xem: Cách xác định góc giữa đường thẳng và mặt phẳng dễ hiểu nhất - IMO2007

Chúng tôi tiếp tục chỉ dẫn những em cơ hội xác lập góc tạo nên vày mặt mũi phẳng lì và đường thẳng liền mạch vô nội dung bài viết tại đây bên trên trang web beyeu.edu.vn. Mời những em hiểu và theo đuổi dõi để sở hữu tầm nhìn cụ thể hơn!

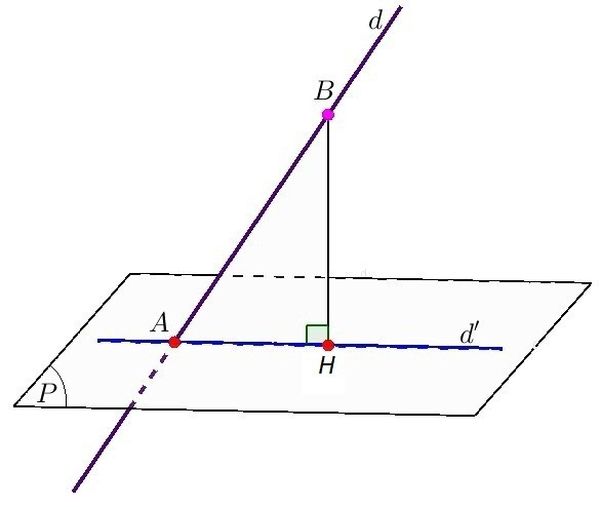
Góc thân ái đường thẳng liền mạch và mặt mũi phẳng lì được xác lập bằng phương pháp đối chiếu với góc thân ái đường thẳng liền mạch và hình chiếu vuông góc của chính nó lên bên trên mặt mũi phẳng lì. Trong tình huống đường thẳng liền mạch d vuông góc với mặt mũi phẳng lì (P), tất cả chúng ta rằng góc thân ái đường thẳng liền mạch d và mặt mũi phẳng lì (P) vày 90 chừng.

Trong tình huống đường thẳng liền mạch d ko vuông góc với mp (P), tất cả chúng ta đo góc thân ái đ/thẳng d và hình chiếu của chính nó, được ký hiệu là d’, lên phía trên mặt phẳng lì (P).

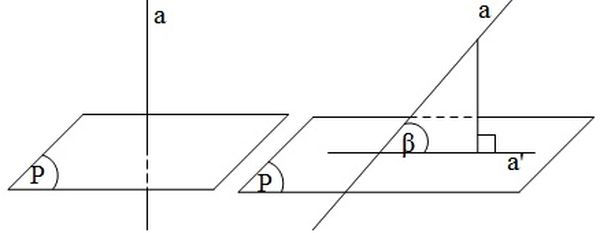
Góc thân ái nhị mặt mũi phẳng

Để gom những em nắm rõ kỹ năng và kiến thức về góc thân ái nhị mặt mũi phẳng lì, thứ nhất tất cả chúng ta tiếp tục dò xét hiểu về định nghĩa của góc thân ái nhị mặt mũi phẳng lì.

Khái niệm: Góc thân ái nhị mặt mũi phẳng lì là gì? Góc thân ái nhị mặt mũi phẳng lì là góc được tạo ra vày hai tuyến phố trực tiếp theo lần lượt vuông góc với nhị mặt mũi phẳng lì bại.

Trong không khí tía chiều, góc thân ái nhị mặt mũi phẳng lì còn được gọi là ‘góc khối’, là phần không khí bị số lượng giới hạn vày nhị mặt mũi phẳng lì. Góc thân ái nhị mặt mũi phẳng lì được đo vày góc thân ái hai tuyến phố trực tiếp bên trên mặt mũi nhị phẳng lì sở hữu nằm trong trực gửi gắm với gửi gắm tuyến của nhị mặt mũi phẳng lì bại.

Tính chất:

• Góc thân ái nhị mặt mũi phẳng lì tuy vậy song vày 0 chừng,
• Góc thân ái nhị mặt mũi phẳng lì trùng nhau vày 0 chừng.

Góc thân ái hai tuyến phố thẳng

Góc thân ái hai tuyến phố trực tiếp a và b vô không khí là góc thân ái hai tuyến phố trực tiếp a’ và b nằm trong trải qua một điểm và theo lần lượt tuy vậy song với a và b.

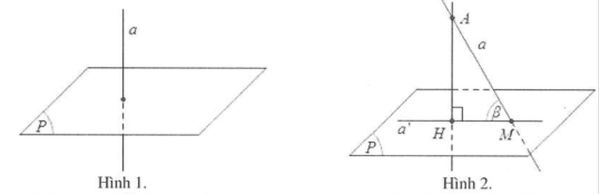
Cách xác lập góc thân ái đường thẳng liền mạch và mặt mũi phẳng

Bước 1: Tìm nút giao nhau O của đường thẳng liền mạch a và mặt mũi phẳng lì (α).

Bước 2: Xây dựng hình chiếu A’ của một điểm A nằm trong đường thẳng liền mạch a xuống mặt mũi phẳng lì (α).

Bước 3: Góc AOA’ = φ là góc thân ái đường thẳng liền mạch a và mp (α).

Lưu ý:

• Để tạo ra hình chiếu A’ của điểm A lên phía trên mặt phẳng lì (α), tất cả chúng ta lựa chọn một đường thẳng liền mạch b vuông góc với mặt mũi phẳng lì (α). Khi bại, đường thẳng liền mạch AA’ // đường thẳng liền mạch b.
• Để tính góc φ, tất cả chúng ta dùng hệ thức lượng vô tam giác vuông OAA’.

Bài tập luyện trắc nghiệm

Cho hình chóp SABCD sở hữu lòng ABCD là hình vuông vắn cạnh a, SAB là tam giác đều và nằm trong mặt mũi phẳng lì vuông góc với lòng, gọi M là trung điểm của SD. Tính góc thân ái CM và mặt mũi phẳng lì (SAB).

A. 90 độ

B. 60 độ

C. 30 độ

D. 45 độ

Xem thêm: Top 99+ hình nền iPhone 14 chất lượng 4k siêu đẹp

Cho hình chóp SABCD sở hữu lòng ABCD là hình vuông vắn cạnh a. Tâm O, SO vuông góc với lòng, gọi M, N là trung điểm của những cạnh SA và BC. thạo góc tạo ra vày MN và mp (ABCD) là 60 chừng. Tính góc thân ái MN và (SBD).

A. 60 độ

B. 45 độ

C. 90 độ

D. 30 độ

Cho lăng trụ ABC.A’B’C’, lòng là tam giác đều cạnh a, AA vuông góc với (ABC). Đường chéo cánh BC¢ của mặt mũi mặt BCC’B’ thích hợp với(ABB’A’) góc 30 chừng . Gọi N là trung điểm của cạnh BB’. Tính góc thân ái MN và (BA’C’).

A. 45 độ

B. 60 độ

C. 90 độ

D. 30 độ

Trong không khí, xác minh này tại đây sai?

A. Nếu tía mặt mũi phẳng lì hạn chế nhau theo đuổi tía gửi gắm tuyến phân biệt thì tía gửi gắm tuyến ấy hoặc đồng quy hoặc song một tuy vậy song cùng nhau.

B. Hai đường thẳng liền mạch phân biệt nằm trong vuông góc với 1 đường thẳng liền mạch thì tuy vậy song cùng nhau.

C. Hai mặt mũi phẳng lì phân biệt nằm trong vuông góc với 1 đường thẳng liền mạch thì tuy vậy song cùng nhau.

D. Cho hai tuyến phố trực tiếp chéo cánh nhau. Có có một không hai một phía phẳng lì chứa chấp đường thẳng liền mạch này và tuy vậy song với đường thẳng liền mạch bại.

Cho tứ diện MNPQ sở hữu nhị tam giác MNP và QNP là nhị tam giác cân nặng theo lần lượt bên trên M và Q. Góc thân ái hai tuyến phố trực tiếp MQ và NP bằng

A. 45 độ

B. 30 độ

C. 60 độ

Xem thêm: Những hình vẽ đen trắng cute đáng yêu mà bạn không thể bỏ qua

D. 90 độ

Bài ghi chép bên trên vẫn cung ứng cho những em những kỹ năng và kiến thức tương quan cho tới góc thân ái đường thẳng liền mạch và mặt mũi phẳng lì. Mong rằng nội dung bài viết vẫn hữu ích so với những em. Hãy chắc hẳn rằng ghi lưu giữ và làm rõ kỹ năng và kiến thức này, những em nhé!

Xem thêm:

• Hướng dẫn xác lập góc thân ái 2 đường thẳng liền mạch rất nhanh vô toán lớp 10
• Tổng thích hợp công thức tính khoảng cách thân ái 2 điểm, kể từ điểm đến chọn lựa mặt mũi phẳng lì, lối thẳng