[TaiMienPhi.Vn] Công thức tính diện tích hình vuông, chu vi hình vuông kèm ví dụ

Hôm ni, Taimienphi.vn nối tiếp update công thức tính chu vi hình vuông, diện tích S hình vuông vắn chuẩn chỉnh theo gót SGK. Các các bạn nằm trong theo gót dõi để hiểu bản thân đang được sử dụng công thức với đúng không nhỉ nhé, kể từ cơ vận dụng nhập tiếp thu kiến thức và việc làm chính chuẩn chỉnh, xử lý yếu tố nhanh gọn.

Cách tiến hành này chung bạn: 
- Có được công thức tính chu vi, diện tích S hình vuông vắn.
- Luyện luyện những bài xích luyện tương quan cho tới tính diện tích S, chu vi hình vuông vắn.
- Có được những cảnh báo Lúc thực hiện bài xích luyện.

Bạn đang xem: [TaiMienPhi.Vn] Công thức tính diện tích hình vuông, chu vi hình vuông kèm ví dụ

Công thức tính diện tích S hình vuông, chu vi hình vuông cũng tương tự nhiều công thức tính chu vi và diện tích S hình chữ nhật, công thức tính diện tích S hình tròn trụ, hình bình hành, hình thang,...đều phải có đặc điểm khá dễ dàng ghi nhớ và dễ dàng vận dụng.

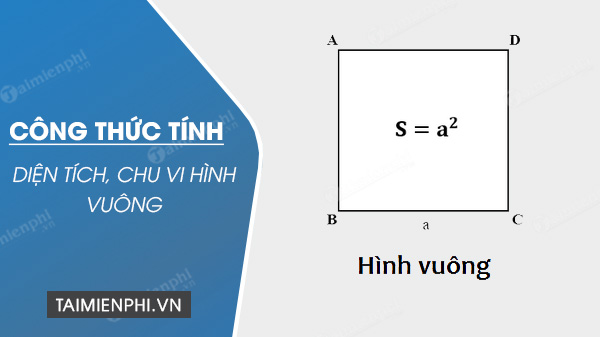
Cách tính diện tích S hình vuông vắn, chu vi hình vuông vắn, công thức tính, ví dụ minh họa

Đặc biệt Lúc dùng phối kết hợp những công thức tính chu vi, diện tích S hình vuông vắn và phương pháp tính diện tích S hình chữ nhật, hình thang, hình bình hành, người giải hoàn toàn có thể đơn giản và dễ dàng xử lý được những Việc phức tạp rộng lớn. Cụ thể công thức tính chu vi và diện tích S hình vuông vắn sẽ tiến hành công ty chúng tôi gửi cho tới người hâm mộ cụ thể như sau đây.

Cách tính diện tích S hình vuông vắn, chu vi hình vuông vắn, công thức tính

1. Công thức tính diện tích S hình vuông

Hình vuông là hình tứ giác với 4 cạnh và 4 góc cân nhau. Các mình muốn tìm hiểu hiểu cụ thể rộng lớn về hình vuông vắn thì hoàn toàn có thể coi thêm thắt bên trên Wikipedia bài viết lách về hình vuông. 

- Khái niệm diện tích S hình vuông: Là bình phương chừng nhiều năm của cạnh nhập hình vuông vắn.
- Cách tính diện tích S hình vuông: S = a x a hoặc S = a²

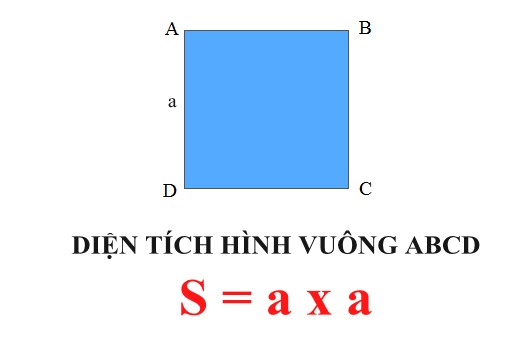
+ a : Độ cài đặt của một cạnh ngẫu nhiên nhập hình vuông vắn.
+ S: Diện tích hình vuông vắn.

Giống như phương pháp tính diện tích S hình vuông vắn, Việc vận dụng công thức tính diện tích S hình vuông vắn cũng tương đối dễ dàng tiến hành Lúc người giải hiểu rằng những số lượng quan trọng.

- Ví dụ:

VD1: Cho hình vuông vắn ABCD với cạnh vị 6cm. Tính diện tích S hình vuông vắn. 
Giải: sít dụng công thức, tớ với diện tích S hình vuông vắn với cạnh 6cm là 6 x 6 = 36 (cm³).
Đáp án: 36cm².

VD2: Cho một hình vuông vắn ABCD chiều nhiều năm những cạnh cân nhau và vị 4 centimet. Hỏi diện tích S của hình vuông vắn ABCD vị bao nhiêu?

Giải:
Theo công thức tính diện tích S hình vuông vắn phía trên, độc giả hoàn toàn có thể vận dụng nhằm tính diện tích S hình vuông vắn ABCD nhập Việc đơn giản và dễ dàng.
Có chiều nhiều năm những cạnh AB = BC = CD = DA = 4cm. Như vậy Lúc phần mềm nhập phương pháp tính diện tích S hình vuông vắn, tớ có:

S = a x a = 4 x 4 = 16 (cm²)

* Công thức tính diện tích S hình vuông vắn lúc biết lối chéo

Hình vuông cũng chính là hình thoi. Do cơ, nếu như hiểu rằng hai tuyến phố chéo cánh hình vuông vắn, chúng ta có thể vận dụng công thức tính diện tích S hình thoi nhập bài xích luyện hình vuông vắn này.

S = 50% (d₁ x d₂)

Trong đó:
- S là diện tích S.
- d₁, d₂: theo thứ tự là lối chéo cánh hình vuông vắn. 

2. Công thức tính chu vi hình vuông

- Khái niệm chu vi hình vuông: Chu vi hình vuông vắn là tổng chừng nhiều năm tư cạnh của chính nó hoặc cấp tư phiên chừng nhiều năm của một cạnh.

- Công thức tính chu vi hình vuông: P = a x 4

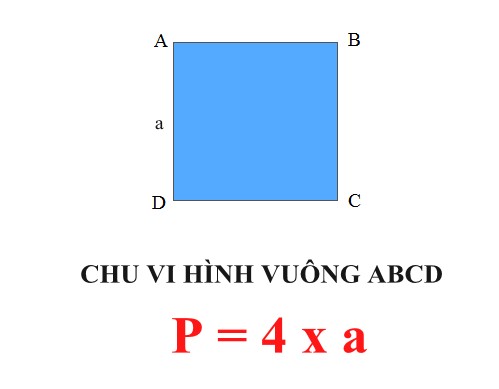
Trong đó:

+ a : chừng cài đặt của một cạnh ngẫu nhiên nhập hình vuông vắn.
+ P: Chu vi hình vuông vắn.

- Ví dụ: Có một hình vuông vắn ABCD với chiều nhiều năm những cạnh cân nhau và vị 5cm. Yêu cầu tính chu vi hình vuông vắn ABCD?

Xem thêm: Tất cả công thức lý 11 học kì 1 : Những kiến thức cơ bản mà bạn cần nắm vững

Giải: sít dụng theo gót công thức tính chu vi hình vuông phía trên, tớ với những cạnh AB = BC = CD = DA = 5 centimet. Như vậy Lúc đi vào công thức tính chu vi hình vuông, tớ có:

P = 5 x 4 = 20 (cm)

(Lưu ý: Công thức tính chu vi, tính diện tích S hình vuông vắn này đều vận dụng mang lại toàn bộ những khối lớp, kể từ lớp 3, lớp 4 trở đi)

3. Tính hóa học và tín hiệu phân biệt của Hình vuông

Hình vuông là một trong hình tứ giác với 4 góc cân nhau và vị 90 chừng, với những cạnh cân nhau. Tính hóa học của hình thoi, hình chữ nhật, hình thang đều phải có ở hình vuông vắn. 

Tính hóa học hình vuông: Hình vuông với đầy đủ đặc điểm của những hình chữ nhật, hình thoi ...

Dấu hiệu phân biệt hình vuông:

- Hình thoi có một góc vuông.
- Hình thoi với hai tuyến phố chéo cánh cân nhau.
- Hình chữ nhật với 1 lối chéo cánh là phân giác của một góc hình chữ nhật.
- Hình chữ nhật với hai tuyến phố chéo cánh vuông góc cùng nhau.
- Hình chữ nhật với nhị cạnh kề cân nhau.

4. Lưu ý về diện tích S, chu vi của hình vuông

Để vẫn tồn tại điểm Lúc thực hiện bài xích đánh giá, bài xích ganh đua tương đương thực hiện bài xích luyện đúng mực, lân cận vận dụng phương pháp tính, công thức tính diện tích S, chu vi, chúng ta nên để ý cho tới đơn vị chức năng đo.
- Với diện tích S, đơn vị chức năng tính toán nón 2 như m², cm².
- Với chu vi, đơn vị chức năng tính toán như thông thường theo gót đề bài xích thể hiện. 

5. Bài luyện về diện tích S, chu vi hình vuông

Bài 1: Cho hình vuông vắn ABCD với chu vi vị 28cm. Tính diện tích S hình vuông vắn ABCD.

Giải:

- Ta với, cạnh AB = BC = CD = DA = 28 : 4 = 7 (cm).
- Diện tích hình vuông vắn ABCD = 7 x 7 = 49 (cm²).

Bài 2: Tính diện tích S hình vuông vắn với chu vi là 32cm.

Giải
- Ta với, chu vi hình vuông vắn là 32, nên những cạnh hình vuông vắn là 32 : 4 = 8 (cm). 
- Diện tích hình vuông vắn là 8 x 8 = 64 (cm²).
Như vậy, diện tích S hình vuông vắn với chu vi là 32cm là 64cm².

Bài 3: Một miếng khu đất hình vuông vắn được không ngừng mở rộng về 1 phía là 5cm thì tớ đạt được chu vi hình chữ nhật là 110m. Tính diện tích S của miếng khu đất sau thời điểm không ngừng mở rộng.

Giải:

Chu vi của miếng khu đất của hình vuông vắn là 110 - 5 x 2 = 100 (cm).

Cạnh miếng khu đất hình vuông vắn là 100 : 4 = 25 (cm).

Chiều nhiều năm miếng khu đất của hình chữ nhật là: 25 + 5 = 30 (cm).

Sau Lúc không ngừng mở rộng thì diện tích S miếng khu đất là 25 x 30 = 750 (cm²).

-----------------HẾT-----------------

Trên đấy là những chỉ dẫn về kiểu cách tính diện tích hình vuông, chu vi hình vuông vắn, công thức tính, mong muốn qua loa nội dung bài viết chúng ta vẫn nắm rõ rộng lớn về kiểu cách tính, công thức tính diện tích S hình vuông vắn, chu vi hình vuông vắn và vận dụng nhập những Việc thực tiễn.

Các các bạn cũng hoàn toàn có thể tìm hiểu thêm thêm thắt về kiểu cách tính diện tích S hình thoi, chu vi hình thoi, công thức tính, ngoài hình vuông vắn thì hình thoi cũng là một trong hình cần thiết, nó đem rất đầy đủ những đặc điểm của hình bình hành, công thức tính diện tích S hình thoi, chu vi hình thoi dễ dàng ghi nhớ, dễ dàng học tập tiếp tục khiến cho bạn xử lý những Việc tương quan cho tới mô hình này.

Xem thêm: Hình Nền OPPO ❤️ Tuyển Tập Ảnh Nền Điện Thoại OPPO - Gấu Đây - Takimart

Chúc chúng ta trở nên công!

Cách tính diện tích S hình thang là một trong trong mỗi công thức khá khó khăn ghi nhớ so với những em học viên lúc học về phần nội dung này, thế cho nên em cần thiết lựa lựa chọn cho bản thân cách thức ghi ghi nhớ hiệu suất cao nhất.

https://beyeu.edu.vn/cach-tinh-dien-tich-hinh-vuong-chu-vi-hinh-vuong-cong-thuc-tinh-nhu-the-nao-22971n.aspx