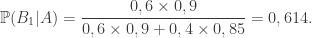beyeu
beyeu
Trang chủ Giáo Dục Bài 1.5: Công thức xác suất đầy đủ, công thức Bayes

Bài 1.5: Công thức xác suất đầy đủ, công thức Bayes

1) Công thức phần trăm đẫy đủ

a) Hệ không hề thiếu những thay đổi cố

Bạn đang xem: Bài 1.5: Công thức xác suất đầy đủ, công thức Bayes

Hệ những thay đổi cố 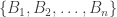\{B_1, B_2,\ldots, B_n\} được gọi là không hề thiếu nếu như thỏa mãn nhu cầu bên cạnh đó nhì điều kiện:

\bullet B_1, B_2,\ldots, B_n là những thay đổi cố xung xung khắc từng song một, tức là B_iB_j=\emptyset với từng i\neq j,

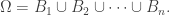
\bullet \Omega=B_1\cup B_2\cup\cdots\cup B_n.

Hệ \{B, \overline{B}\} là một trong hệ không hề thiếu, nhập cơ B là một trong thay đổi cố ngẫu nhiên.

 b) Công thức phần trăm đẫy đủ

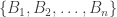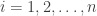Giả sử \{B_1, B_2,\ldots, B_n\} là hệ không hề thiếu những thay đổi cố với \Bbb P(B_i)>0 với từng i=1,2,\ldots,n. Khi cơ với ngẫu nhiên thay đổi cố A, tớ có

\Bbb P(A)=\Bbb P(B_1)\Bbb P(A | B_1)+\Bbb P(B_2)\Bbb P(A | B_2)+\cdots+\Bbb P(B_n)\Bbb P(A | B_n).

Ví dụ 1:

Có 3 vỏ hộp như là nhau. Hộp loại nhất đựng 10 thành phầm, nhập cơ với 6 chủ yếu phẩm, vỏ hộp loại nhì đựng 15 thành phầm, nhập cơ với 10 chủ yếu phẩm, vỏ hộp loại tía đựng đôi mươi thành phầm, nhập cơ với 15 chủ yếu phẩm. Lấy tình cờ một vỏ hộp và kể từ cơ lấy tình cờ một thành phầm. Tìm phần trăm nhằm lấy được chủ yếu phẩm.

Lời giải: 

Ký hiệu 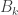B_k là thay đổi cố: “Sản phẩm mang ra nằm trong vỏ hộp loại 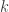k“, k=1, 2, 3 và A là thay đổi cố: “Lấy được chủ yếu phẩm”.

Khi cơ 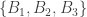\{B_1, B_2, B_3\} là hệ không hề thiếu những thay đổi cố và

\Bbb P(B_1)=\displaystyle\frac{1}{3}, \Bbb P(B_2)=\displaystyle\frac{1}{3}, \Bbb P(B_3)=\displaystyle\frac{1}{3},

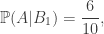
\Bbb P(A | B_1)=\displaystyle\frac{6}{10},

\Bbb P(A | B_2)=\displaystyle\frac{10}{15},

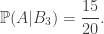
\Bbb P(A | B_3)=\displaystyle\frac{15}{20}.

Theo công thức xác suất đầy đủ

\Bbb P(A)=\Bbb P(B_1)\Bbb P(A | B_1)+\Bbb P(B_2)\Bbb P(A | B_2)+\Bbb P(B_3)\Bbb P(A | B_3)

Thay nhập tớ thu được

\Bbb P(A)=\displaystyle\frac{1}{3}\times \displaystyle\frac{6}{10}+\displaystyle\frac{1}{3}\times \displaystyle\frac{10}{15}+\displaystyle\frac{1}{3}\times \displaystyle\frac{15}{20}

   =\displaystyle\frac{124}{180}

   =\displaystyle\frac{31}{45}

Vậy phần trăm nhằm lấy được chủ yếu phẩm là \displaystyle\frac{31}{45}.

Ví dụ 2:  

Từ một vỏ hộp chứa chấp 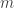m trái khoáy cầu Trắng và 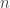n trái khoáy cầu đen thui, người tớ rút tình cờ ko hoàn trả từng trái khoáy một nhì đợt. Tính phần trăm nhằm trái khoáy lấy đợt loại nhì là Trắng.

Lời giải: 

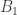Ký hiệu A là thay đổi cố: “Lần loại nhì rút được trái khoáy cầu trắng”, B_1 là thay đổi cố: “Lần loại nhất rút được trái khoáy cầu trắng”, B_2 là thay đổi cố: “Lần loại nhất rút được trái khoáy cầu đen”.

Ta có

\Bbb P(B_1)=\displaystyle\frac{m}{m+n}, \Bbb P(B_2)=\displaystyle\frac{n}{m+n},

\Bbb P(A|B_1)=\displaystyle\frac{m-1}{m+n-1}, \Bbb P(A|B_2)=\displaystyle\frac{m}{m+n-1}.

 Vì \{B_1, B_2\} là một trong hệ không hề thiếu nên bám theo công thức xác suất đầy đủ

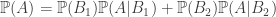
  \Bbb P(A)=\Bbb P(B_1)\Bbb P(A|B_1)+\Bbb P(B_2)\Bbb P(A|B_2)

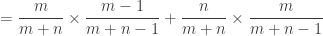
    =\displaystyle\frac{m}{m+n}\times\displaystyle\frac{m-1}{m+n-1}+\displaystyle\frac{n}{m+n}\times\displaystyle\frac{m}{m+n-1}

    =\displaystyle\frac{m(m-1)+mn}{(m+n)(m+n-1)}

    =\displaystyle\frac{m(m+n-1)}{(m+n)(m+n-1)}

    =\displaystyle\frac{m}{m+n}.

Vậy phần trăm nhằm trái khoáy lấy đợt loại nhì là Trắng là 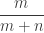\displaystyle\frac{m}{m+n}.

Ví dụ 3: 

Có 10 cái túi như sau:

4 túi loại 1, trong những túi loại 1 chứa chấp 6 viên bi Trắng và 4 viên bi đen thui,

2 túi loại 2, trong những túi loại 2 chứa chấp 3 viên bi Trắng và 7 viên bi đen thui,

1 túi loại 3, trong những túi loại 3 chứa chấp 7 viên bi Trắng và 3 viên bi đen thui,

3 túi loại 4, trong những túi loại 4 chứa chấp 4 viên bi Trắng và 6 viên bi đen thui.

Chọn tình cờ 1 cái túi rồi lấy tình cờ 2 viên bi. Tính phần trăm nhằm lấy được nhì viên bi nằm trong color.

Lời giải:  

Ký hiệu 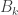B_k là thay đổi cố “chọn được túi loại 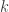k“, k=1, 2, 3, 4 và A là thay đổi cố “lấy được nhì viên bi nằm trong màu”.

Khi cơ \{B_1, B_2, B_3, B_4\} là hệ không hề thiếu những thay đổi cố và tớ có

\Bbb P(B_1)=\displaystyle\frac{4}{10}, \Bbb P(B_2)=\displaystyle\frac{2}{10},

\Bbb P(B_3)=\displaystyle\frac{1}{10}, \Bbb P(B_4)=\displaystyle\frac{3}{10},

\Bbb P(A | B_1)=\displaystyle\frac{C_6^2+C_4^2}{C_{10}^2}=\displaystyle\frac{21}{45},

\Bbb P(A | B_2)=\displaystyle\frac{C_3^2+C_7^2}{C_{10}^2}=\displaystyle\frac{24}{45},

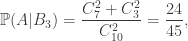
\Bbb P(A | B_3)=\displaystyle\frac{C_7^2+C_3^2}{C_{10}^2}=\displaystyle\frac{24}{45},

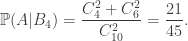
\Bbb P(A | B_4)=\displaystyle\frac{C_4^2+C_6^2}{C_{10}^2}=\displaystyle\frac{21}{45}.

Xem thêm: TOP ảnh gái xinh mặc bikini mỏng siêu nhỏ xuyên thấu lọt khe

Theo công thức xác suất đầy đủ

\Bbb P(A)=\Bbb P(B_1)\Bbb P(A | B_1)+\Bbb P(B_2)\Bbb P(A | B_2)+\Bbb P(B_3)\Bbb P(A | B_3)+\Bbb P(B_4)\Bbb P(A | B_4)

Thay nhập tớ được

\Bbb P(A)=\displaystyle\frac{4}{10}\times \displaystyle\frac{21}{45}+\displaystyle\frac{2}{10}\times \displaystyle\frac{24}{45}+\displaystyle\frac{1}{10}\times \displaystyle\frac{24}{45}+\displaystyle\frac{3}{10}\times \displaystyle\frac{21}{45}

  =\displaystyle\frac{219}{450}.

Vậy

\Bbb P(A)=\displaystyle\frac{219}{450}.

 Ví dụ 4: 

Có nhì dòng sản phẩm vỏ hộp. Hộp loại nhất với 4 bi Trắng và 5 bi đen thui. Hộp loại nhì với 5 bi Trắng và 4 bi đen thui. Chọn tình cờ 3 viên bi ở vỏ hộp loại nhất cho vô vỏ hộp loại nhì rồi tiếp sau đó lựa chọn tình cờ một viên bi ở vỏ hộp loại nhì rời khỏi. Tính phần trăm nhằm lấy được bi Trắng kể từ vỏ hộp loại nhì.

Lời giải:

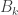Gọi A là thay đổi cố: ”Lấy được bi Trắng kể từ vỏ hộp loại hai”, B_k là thay đổi cố: ”Trong 3 viên bi mang ra kể từ vỏ hộp loại nhất với 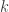k bi trắng”, k=0, 1, 2, 3.

Khi đó \{B_0, B_1, B_1, B_3\} là hệ không hề thiếu những thay đổi cố và tớ có

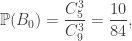
\Bbb P(B_0)=\displaystyle\frac{C_5^3}{C_9^3}=\displaystyle\frac{10}{84},

\Bbb P(B_1)=\displaystyle\frac{C_4^1C_5^2}{C_9^3}=\displaystyle\frac{40}{84},

\Bbb P(B_2)=\displaystyle\frac{C_4^2C_5^1}{C_9^3}=\displaystyle\frac{30}{84},

\Bbb P(B_3)=\displaystyle\frac{C_4^3}{C_9^3}=\displaystyle\frac{4}{84}.

Theo công thức xác suất đầy đủ

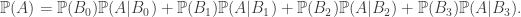
\Bbb P(A)=\Bbb P(B_0)\Bbb P(A | B_0)+\Bbb P(B_1)\Bbb P(A | B_1)+\Bbb P(B_2)\Bbb P(A | B_2)+\Bbb P(B_3)\Bbb P(A | B_3).

Dễ thấy

\Bbb P(A | B_0)=\displaystyle\frac{5}{12}, \Bbb P(A | B_1)=\displaystyle\frac{6}{12},

\Bbb P(A | B_2)=\displaystyle\frac{7}{12}, \Bbb P(A | B_3)=\displaystyle\frac{8}{12}.

Thay những độ quý hiếm này nhập tớ được

\Bbb P(A)=\displaystyle\frac{10}{84}\times\displaystyle\frac{5}{12}+\displaystyle\frac{40}{84}\times\displaystyle\frac{6}{12}+\displaystyle\frac{30}{84}\times\displaystyle\frac{7}{12}+\displaystyle\frac{4}{84}\times\displaystyle\frac{8}{12}

  =\displaystyle\frac{532}{1008}

  =\displaystyle\frac{19}{36}.

Vậy phần trăm cần thiết mò mẫm là \displaystyle\frac{19}{36}.

Ví dụ 5:

Trong một chiếc vỏ hộp với 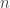n thành phầm, tớ cho vô dòng sản phẩm vỏ hộp cơ một thành phầm chất lượng tốt tiếp sau đó lấy tình cờ rời khỏi một thành phầm. Tính phần trăm nhằm thành phầm mang ra là chất lượng tốt nếu như từng fake thiết về hiện trạng cấu trở thành thuở đầu của vỏ hộp là đồng phần trăm.

Lời giải:

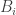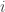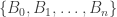Gọi A là thay đổi cố: “Lấy được thành phầm tốt”, B_i là thay đổi cố: “Lúc thuở đầu vỏ hộp với i thành phầm tốt”, i=0,1,\ldots,n. Khi đó \{B_0, B_1,\ldots, B_n\} là hệ không hề thiếu những thay đổi cố.

Theo fake thiết

\Bbb P(B_i)=\displaystyle\frac{1}{n+1}, i=0,1,\ldots,n.

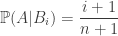Ta với \Bbb P(A | B_i)=\displaystyle\frac{i+1}{n+1} với từng i=0,1,\ldots,n.

Theo công thức xác suất đầy đủ

\Bbb P(A)=\displaystyle\sum\limits_{i=0}^{n}\Bbb P(B_i)\Bbb P(A | B_i).

Thay nhập tớ được

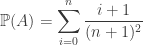
\Bbb P(A)=\displaystyle\sum\limits_{i=0}^{n}\displaystyle\frac{i+1}{(n+1)^2}

   =\displaystyle\frac{1+2+\cdots+(n+1)}{(n+1)^2}

   =\displaystyle\frac{(n+1)(n+2)}{2(n+1)^2}

   =\displaystyle\frac{n+2}{2(n+1)}.

2) Công thức Bayes

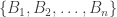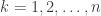Giả sử \Bbb P(A)>0 và \{B_1, B_2,\ldots, B_n\} là hệ không hề thiếu những thay đổi cố với \Bbb P(B_k)>0 với từng k=1,2,\ldots,n. Khi đó với từng 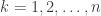k=1,2,\ldots,n, tớ có

\Bbb P(B_k | A)=\displaystyle\frac{\Bbb P(B_k)\Bbb P(A | B_k)}{\Bbb P(B_1)\Bbb P(A | B_1)+\Bbb P(B_2)\Bbb P(A | B_2)+\cdots+\Bbb P(B_n)\Bbb P(A | B_n)}.

Ví dụ 6:

Dây chuyền thi công ráp cảm nhận được những cụ thể tự nhì máy phát triển. Trung bình máy loại nhất hỗ trợ 60% cụ thể, máy loại nhì hỗ trợ 40% cụ thể. Khoảng 90% cụ thể tự máy loại nhất phát triển là đã đạt chi tiêu chuẩn chỉnh, còn 85% cụ thể tự máy loại nhì phát triển là đã đạt chi tiêu chuẩn chỉnh. Lấy tình cờ kể từ dây chuyền sản xuất một thành phầm, thấy nó đạt chi tiêu chuẩn chỉnh. Tìm phần trăm nhằm thành phầm cơ tự máy loại nhất phát triển.

Lời giải:

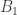Gọi A là thay đổi cố: “Chi tiết lấy kể từ dây chuyền sản xuất đạt chi tiêu chuẩn”, B_1 là thay đổi cố: “Chi tiết tự máy loại nhất sản xuất” và B_2 là thay đổi cố: “Chi tiết tự máy loại nhì sản xuất”. Ta cần thiết tính phần trăm \Bbb P(B_1|A).

Theo công thức Bayes

\Bbb P(B_1|A)=\displaystyle\frac{\Bbb P(B_1)\Bbb P(A|B_1)}{\Bbb P(B_1)\Bbb P(A|B_1)+\Bbb P(B_2)\Bbb P(A|B_2)}.

Theo ĐK bài bác toán

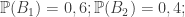
\Bbb P(B_1)=0,6; \Bbb P(B_2)=0,4;

Xem thêm: 7 Hằng Đẳng Thức Đáng Nhớ Và Hệ Quả

\Bbb P(A|B_1)=0,9; \Bbb P(A|B_2)=0,85.

Thay nhập tớ có

\Bbb P(B_1|A)=\displaystyle\frac{0,6\times 0,9}{0,6\times 0,9+0,4\times 0,85}=0,614.

BÀI VIẾT NỔI BẬT

Bài tập chứng minh tam giác nội tiếp dễ hiểu - HOCMAI

  Trong chương trình học toán lớp 9, bài tập chứng minh tam giác nội tiếp đường tròn hay bài tập chứng minh đường tròn ngoại tiếp tam giác là bài ăn điểm trong những đề kiểm tra. Các em học sinh chỉ cần nắm chắc lý thuyết, đọc kỹ đề bài là có thể …

Danh sách những hot girl Trung Quốc xinh đẹp nhất

Khám phá bức tranh tuyệt vời với hình ảnh của những hot girl Trung Quốc đẹp nhất. Với dân số đông nhất thế giới, Trung Quốc là quê hương của nhiều hot girl nổi tiếng. Nếu bạn là fan hâm mộ, những hình ảnh này chắc chắn sẽ làm cho trái tim bạn đắm đuối. Hãy cùng nhau chiêm ngưỡng!

Bài tập phương trình hóa học lớp 8

Bài tập phương trình hóa học lớp 8 được biến soạn có đáp án, hy vọng tài liệu giúp ích cho các bạn học sinh củng cố luyện tập biết cách cân bằng phường trình phản ứng.

10 hình ảnh hoa sen trắng buồn ngọt ngào khiến lòng rung động

Chủ đề hình ảnh hoa sen trắng buồn Hình ảnh hoa sen trắng buồn mang đến cho chúng ta không chỉ nỗi buồn mà còn khơi dậy những tâm trạng sâu sắc và ý nghĩa tình cảm. Một sự kết hợp đặc biệt giữa gam màu trắng và đen, những bông hoa sen trắng đám tang buồn thể hiện sự trang trọng, thành kính và tôn trọng đối với những người đã ra đi. Hãy cùng lan tỏa thông điệp yêu thương và tôn vinh sự hiện diện của những người thân yêu đã mất trong những bức hình này.