Diện tích tam giác là 1 trong trong mỗi công thức toán học tập nhưng mà các bạn sẽ được học tập và vận dụng thật nhiều trong số bài xích tập dượt của môn Toán học. Để tính được diện tích S hình tam giác, sở hữu thật nhiều công thức và cơ hội vận dụng không giống nhau. Muốn tăng kỹ năng suy nghĩ và đo lường và tính toán không gian hình tam giác thì chớ bỏ dở nội dung bài viết này.
Dưới trên đây, The Dewey Schools tiếp tục tổ hợp những công thức tính diện tích S tam giác vừa đủ nhất.
Bạn đang xem: Tổng hợp công thức tính diện tích tam giác đầy đủ nhất 2023
Trước khi cút nhập tính diện tích S tam giác, tất cả chúng ta cần thiết hiểu rộng lớn về khái niệm hình tam giác và ghi ghi nhớ những đặc điểm quan trọng của hình tam giác.
Định nghĩa
Hình tam giác là 1 trong hình học tập cơ phiên bản nhập toán học tập và hình học tập. Nó là 1 trong nhiều giác sở hữu tía cạnh và tía đỉnh. Các cạnh của tam giác nối những đỉnh cùng nhau và những góc trong những cạnh tạo ra trở thành những góc của tam giác.
Hình tam giác là gì
Phân loại
Có một trong những cơ hội phân loại tam giác dựa vào những đặc điểm không giống nhau của nó:
1. Theo cạnh
- Tam giác đều: Có tía cạnh đều bằng nhau và tía góc đều bằng nhau (60 độ).
- Tam giác cân: Có tối thiểu nhị cạnh đều bằng nhau.
- Tam giác vuông: Có một góc vuông (90 độ).
2. Theo góc
- Tam giác nhọn: Có tía góc nhọn, tức là những góc đều nhỏ rộng lớn 90 chừng.
- Tam giác tù: Có một góc tù, tức là 1 trong góc to hơn 90 chừng.
- Tam giác vuông: Đã rằng phía trên, sở hữu một góc vuông.
3, Theo chừng nhiều năm những cạnh
- Tam giác thường: Có tía cạnh và tía góc đều ko đều bằng nhau.
- Tam giác đều, cân nặng, vuông, tù…
>>Xem thêm: Học môn đương nhiên nên đua khối nào? Các ngành học tập triển vọng năm 2023
Tính chất
Hình tam giác có tương đối nhiều đặc điểm cần thiết và xứng đáng lưu ý nhập hình học tập và toán học tập. Dưới đó là một trong những đặc điểm cơ phiên bản của tam giác, hãy ghi ghi nhớ nhằm thực hiện bài xích tập dượt một cơ hội hiệu quả:
- Tổng những góc nhập tam giác: Tổng của tía góc nhập một tam giác luôn luôn bởi vì 180 chừng. Công thức này được gọi là Định lý tổng những góc nhập tam giác.
- Định lý góc ngoài tam giác: Mỗi góc ngoài của tam giác bởi vì tổng nhị góc nhập tam giác ko chứa chấp nó. Hay rằng cách thứ hai, từng góc ngoài bởi vì góc phần sót lại khi tớ vô hiệu hóa nó ngoài tam giác.
- Bất đẳng thức tam giác: Trong một tam giác, tổng chừng nhiều năm nhị cạnh ngẫu nhiên luôn luôn to hơn chừng nhiều năm cạnh sót lại. Nếu tam giác sở hữu cạnh đầy đủ nhiều năm, tổng nhị cạnh ngắn lại tiếp tục to hơn cạnh nhiều năm nhất.
- Định lý Pythagoras: Đối với tam giác vuông, bình phương chừng nhiều năm cạnh huyền (cạnh đối lập góc vuông) bởi vì tổng bình phương chừng nhiều năm nhị cạnh góc vuông (được gọi là tấp tểnh lý Pythagoras).
- Đoạn phân giác của tam giác: Đoạn trực tiếp từ là một đỉnh của tam giác tới điểm bên trên cạnh đối lập, sao mang lại phân chia cạnh trở thành nhị đoạn sở hữu tỷ số bởi vì tỷ số chừng nhiều năm nhị cạnh sót lại, này đó là đoạn phân giác.
- Các trung điểm nhập tam giác: Ba đoạn trực tiếp nối những đỉnh của tam giác cho tới những điểm trung điểm của cạnh đối lập là tía đoạn trực tiếp có tính nhiều năm đều bằng nhau và kí thác nhau bên trên một điểm (gọi là trọng tâm của tam giác).
- Tính hóa học chu vi và diện tích S: Tam giác sở hữu chu vi bởi vì tổng chừng nhiều năm tía cạnh của chính nó. Diện tích của tam giác hoàn toàn có thể được xem bởi vì nhiều cách thức không giống nhau như Công thức diện tích S Heron hoặc dùng độ cao và cạnh ứng.
Đây đơn giản một trong những đặc điểm cơ phiên bản của tam giác. Tam giác là 1 trong hình học tập nhiều diện phong phú và đa dạng, có tương đối nhiều đặc điểm không giống nhau và được phân tích thâm thúy nhập hình học tập và những nghành nghề dịch vụ toán học tập tương quan.
Tổng thích hợp 6 công thức tính diện tích S tam giác chi tiết
Để tính diện tích S tam giác, phụ thuộc Điểm sáng phân loại của tam giác cơ hoàn toàn có thể vận dụng được không ít công thực tính không giống nhau. Dưới đó là tổ hợp 6 công thức tính diện tích S hình tam giác chi tiết:
Tổng thích hợp 6 công thức tính diện tích S tam giác chi tiết
Cách tính diện tích S tam giác thông thường abc chủ yếu xác
Tam giác thông thường là tam giác có tính nhiều năm những cạnh không giống nhau và số đo 3 góc cũng không giống nhau.
Công thức tính S tam giác thông thường abc được xem như sau: Độ nhiều năm của một cạnh ngẫu nhiên nhân với độ cao ứng của cạnh cơ và phân chia 2.
Cách tính diện tích S tam giác thông thường abc chủ yếu xác
Trong đó:
- a là chừng nhiều năm của một cạnh bất kỳ
- h là độ cao hạ kể từ đỉnh tam giác xuống cạnh a đó
Ví dụ: Tam giác ABC có tính nhiều năm cạnh a là 6cm, độ cao h hạ kể từ đỉnh xuống cạnh A có tính nhiều năm là 4 centimet. Vậy diện tích S tam giác ABC được xem như sau: ½ (6*4) = 12 cm²
Kiến thức nâng cao: Để tính diện tích S tam giác thông thường abc, dựa vào những vấn đề đã có sẵn, bạn cũng có thể vận dụng một trong những công thức nâng lên sau:
- Sử dụng công thức diện tích S Heron
Đối với tam giác ABC sở hữu tía cạnh a, b và c, và nửa chu vi là p (p = (a + b + c) / 2), diện tích S tam giác được xem bởi vì công thức Heron:
S(ABC) = √(p * (p – a) * (p – b) * (p – c))
- Sử dụng tấp tểnh lý Sine
Nếu chúng ta biết một góc và nhị cạnh nhập tam giác ABC, bạn cũng có thể dùng tấp tểnh lý Sine nhằm tính diện tích S. Định lý Sine mang lại biết:
S(ABC) = (1/2) * a * b * sin(C)
Trong cơ C là góc thân ái nhị cạnh a và b
Cách tính S tam giác vuông kèm cặp ví dụ
Tam giác vuông là tam giác sở hữu một góc vuông. Góc vuông là góc nhưng mà nhị cạnh tạo ra trở thành nó vuông góc cùng nhau, tức là bọn chúng bắt gặp nhau sao mang lại nút giao của bọn chúng tạo ra trở thành một góc vuông 90 chừng.
Công thức tính diện tích S tam giác vuông như sau: Độ nhiều năm nhị cạnh góc vuông nhân cùng nhau và phân chia mang lại 2
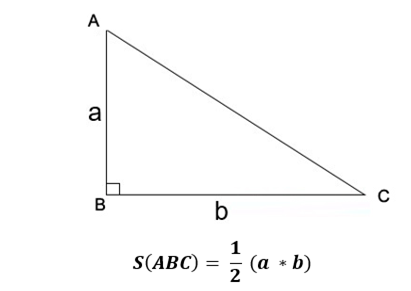
Trong đó: a, b là chừng nhiều năm của nhị cạnh góc vuông
Ví dụ: Tam giác vuông ABC có tính nhiều năm 2 cạnh góc vuông thứu tự là 5 centimet và 8 centimet. Diện tích tam giác ABC thời điểm hiện tại được xem như sau: ½ (5 * 8) = trăng tròn cm²
Công thức diện tích S tam giác vuông cân nặng ăm ắp đủ
Tam giác vuông cân nặng là 1 trong mô hình tam giác vuông quan trọng, sở hữu nhị cạnh có tính nhiều năm đều bằng nhau, tạo ra trở thành góc vuông, và mặt khác cũng chính là nhị cạnh góc vuông
Công thức tính diện tích S tam giác vuông cân nặng được xem như sau: Độ nhiều năm của một cạnh góc vuông bình phương tiếp sau đó phân chia 2.
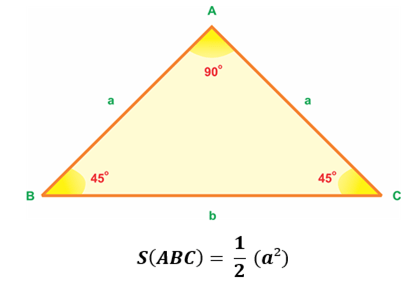
Công thức diện tích S tam giác vuông cân nặng ăm ắp đủ
Trong đó: a là chừng nhiều năm nhị cạnh góc vuông đều bằng nhau.
Ví dụ: Tam giác vuông cân nặng ABC có tính nhiều năm nhị cạnh góc vuông là 4 centimet. Diện tích tam giác ABC được xem như sau: S(ABC) = ½ (4²) = 8 cm²
Cách tính diện tích S tam giác cân nặng đơn giản
Tam giác cân nặng là 1 trong mô hình tam giác quan trọng, sở hữu nhị cạnh có tính nhiều năm đều bằng nhau và nhị góc đối lập với những cạnh này cũng đều bằng nhau.
Công thức tính diện tích S tam giác cân nặng được xem như sau: Độ nhiều năm cạnh sót lại nhân với độ cao ứng của cạnh cơ rồi phân chia 2.
Trong đó:
- a là chiều nhiều năm cạnh sót lại không giống 2 cạnh có tính nhiều năm đều bằng nhau (BC)
- h là độ cao nối kể từ đỉnh góc đối lập của cạnh cơ xuống lòng (AM)
Ví dụ: Cho tam giác cân nặng ABC có tính nhiều năm 2 cạnh AB và AC đều bằng nhau, cạnh BC có tính nhiều năm là 9 centimet. Chiều cao nối kể từ đỉnh A xuống BC có tính nhiều năm là 5 centimet. Diện tích tam giác ABC cân nặng được xem như sau: S(ABC) = ½ (9 * 5) = 22,5 cm²
Công thức tính diện tích S tam giác đều cạnh a
Tam giác đều là 1 trong mô hình tam giác quan trọng, sở hữu tía cạnh và tía góc đều nhau. Tức là toàn bộ những cạnh của tam giác đều phải có chừng nhiều năm đều bằng nhau và toàn bộ những góc của tam giác đều phải có kích thước và đúng là 60 chừng.
Công thức tính diện tích S tam giác đều cạnh a được xem như sau: Độ nhiều năm của một cạnh ngẫu nhiên nhân với độ cao ngẫu nhiên và phân chia 2.
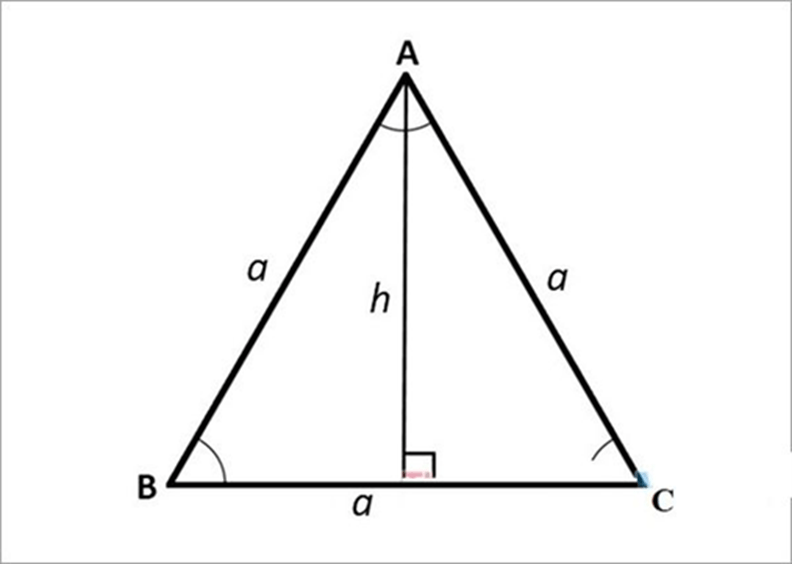
Công thức tính diện tích S tam giác đều cạnh a
Trong đó:
- a là chiều nhiều năm của một cạnh bất kỳ
- h là độ cao ngẫu nhiên (trong tam giác đều, độ cao của những cạnh đều bởi vì nhau)
Ví dụ: Tam giác đều ABC sở hữu những cạnh đều bằng nhau và bởi vì 7cm, độ cao hạ kể từ đỉnh A xuống cạnh BC là 6 centimet. Diện tích tam giác ABC được xem như sau:
S(ABC) = ½ (7 * 6) = 21 cm²
Công thức tính diện tích S tam giác nhập Oxyz
Trong hệ tọa chừng Oxyz, tam giác là 1 trong nhiều giác tía cạnh ở trong không khí tía chiều, được xác lập bởi vì tía điểm ko và một đường thẳng liền mạch. Các điểm này được màn trình diễn bởi vì những tọa chừng (x, hắn, z), nhập cơ x, hắn và z là những số thực thể hiện nay địa điểm của điểm nhập không khí.
Công thức tính diện tích S tam giác nhập hệ trục tọa chừng Oxyz được xem như sau: Diện tích tam giác ABC được xem bởi vì nửa độ quý hiếm vô cùng của tích hạng tía của nhị vectơ AB và AC:
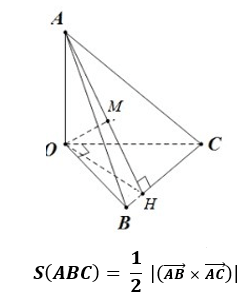
Trong đó: AB và AC là nhị vectơ được màn trình diễn bên trên trục Oxyz
Ví dụ: Trên hệ trục tọa chừng mang lại tam giác ABC sở hữu 3 điểm A(-1; 1; 2), B(1; 2; 3), C(3; – 2; 0). Diện tích tam giác ABC được xem như sau:
Các dạng bài xích thói quen diện tích S tam giác thông thường gặp
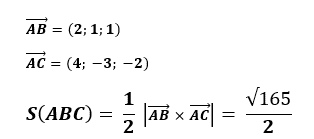
Từ công thức tính diện tích S tam giác sẽ sở hữu được thật nhiều dạng bài xích tập dượt nhưng mà bạn phải chú ý vì thế tiếp tục thông thường xuyên bắt gặp trong tương đối nhiều bài xích tập dượt. Ghi ghi nhớ những công thức phía trên và thám thính hiểu những dạng bài xích tập dượt sau đây sẽ hỗ trợ nhỏ xíu hoàn toàn có thể nhanh gọn giải quyết và xử lý những bài xích tập:
Bài thói quen S tam giác lúc biết chiều nhiều năm cạnh lòng và độ cao h
Đây là dạng bài xích tập dượt khá dễ dàng, vận dụng công thức tính diện tích S tam giác cơ phiên bản là tiếp tục đã tạo ra thành phẩm chủ yếu xác: :
S (ABC) = ½ (a*h).
Bài tập dượt minh họa: Cho tam giác ABC có tính nhiều năm cạnh BC là 40 centimet, độ cao ứng với cạnh lòng BC có tính nhiều năm là 5 centimet. Tính diện tích S tam giác ABC
Lời giải: S(ABC) = ½ (BC * h) = ½ (40 * 5) = 100 cm²
Bài thói quen S tam giác lúc biết chừng nhiều năm những cạnh
Với dạng bài xích tập dượt này, tớ hoàn toàn có thể giải Theo phong cách là vận dụng công thức Heron:
S(ABC) = √(p * (p – a) * (p – b) * (p – c))
Trong cơ, tam giác ABC sở hữu tía cạnh a, b và c, và nửa chu vi là p (p = (a + b + c) / 2)
Bài thói quen S tam giác đều lúc biết chừng nhiều năm một cạnh
Khi biết chừng nhiều năm một cạnh nhập tam giác đều, đồng nghĩa tương quan với việc tớ biết chừng nhiều năm của tất cả tía cạnh và biết 3 góc đều bằng nhau và bởi vì 60 chừng. Đối với dạng bài xích tập dượt này hoàn toàn có thể tính theo gót 3 cơ hội như sau:
- Cách 1: kề dụng công thức Heron
- Cách 2: Định lý Cosine, diện tích S tam giác tiếp tục là: S(ABC) = (1/2) * a² * sin(60⁰).
- Cách 3: Đi thám thính độ cao của tam giác. Lúc này, độ cao sẽ tiến hành tính theo gót công thức như sau: h = a² – (a/2)² . Sau khi tính được h, vận dụng công thức tính diện tích S như thông thường là rời khỏi.
Bài thói quen diện tích S tam giác nhập tọa chừng Oxyz
Trong hệ tọa chừng Oxyz, mang lại 3 điểm
- A (x1; y1; z1)
- B (x2; y2; z2)
- C (x3; y3; z3)
Dựa bên trên công thức:
Xem thêm: Chu vi xích đạo của trái đất
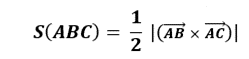
Ta tìm kiếm được 2 vecto AB và AC bằng phương pháp trừ những điểm x;y;z của 2 điểm A với B và A với C
Sau khi tìm kiếm được tọa chừng (x; y; z) của 2 vecto cơ tớ tổ chức nhân 2 vecto lại cùng nhau và phân chia mang lại 2 là rời khỏi thành phẩm.
Tìm chừng nhiều năm cạnh huyền nhập tam giác vuông lúc biết diện tích S và cạnh a
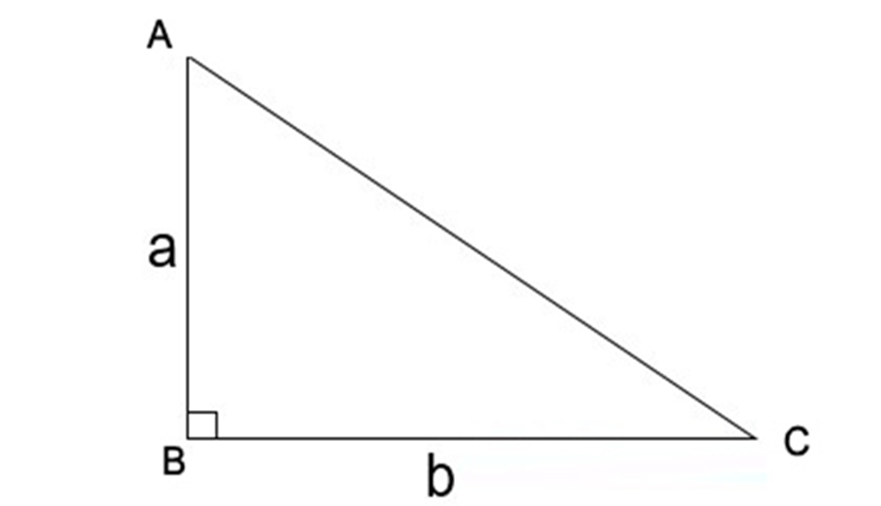
Công thức tính diện tích S tam giác vuông như sau: S (ABC) = ½ (a * b).
Để tìm kiếm được chừng nhiều năm cạnh huyền, tớ tổ chức công việc như sau:
- Tìm chừng nhiều năm cạnh b = (S(ABC) * 2) / a
- Sau lúc biết chừng nhiều năm cạnh b, tớ vận dụng công thức Pytago: c² = a² + b²
- Tìm được c² ta sẽ sở hữu được thành phẩm của c là cạnh huyền của tam giác vuông ABC
Tìm S tam giác lúc biết chu vi và nửa đường kính đàng tròn xoe nội tiếp
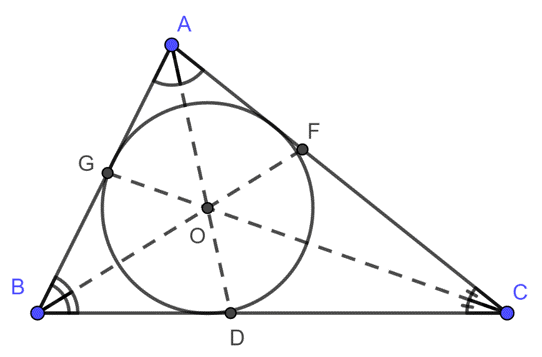
Để tính diện tích S tam giác lúc biết chu vi (P) và nửa đường kính đàng tròn xoe nội tiếp (r), tớ dùng một công thức tương quan cho tới tam giác và đàng tròn xoe nội tiếp.
Đặt a, b và c thứu tự là tía cạnh của tam giác và R là nửa đường kính đàng tròn xoe nước ngoài tiếp tam giác (được tính bởi vì tía đỉnh của tam giác). Ta sở hữu những quan hệ sau:
- Diện tích tam giác (S) và nửa đường kính đàng tròn xoe nước ngoài tiếp (R):
S = (abc) / (4R)
- Diện tích tam giác (S) và chu vi (P):
S = (P * r) / 2
Trong cơ, P.. là chu vi tam giác và r là nửa đường kính đàng tròn xoe nội tiếp tam giác.
Bây giờ, tất cả chúng ta hoàn toàn có thể giải nhị công thức này nhằm thám thính diện tích S tam giác (S):
Từ công thức (1):
(P * r) / 2 = (abc) / (4R)
Từ công thức (2):
S = (P * r) / 2
Kết thích hợp nhị công thức trên:
S = ((abc) / (4R)) / 2
S = (abc) / (8R)
Vì vậy, diện tích S tam giác (S) hoàn toàn có thể được xem bởi vì công thức S = (abc) / (8R), lúc biết chu vi (P) và nửa đường kính đàng tròn xoe nội tiếp (r) của tam giác.
Một số bài xích thói quen diện tích S tam giác điển hình nổi bật kèm cặp điều giải chi tiết
Dựa nhập công thức và những dạng bài xích tập dượt bên trên, chúng ta tiếp tục bắt được phương pháp tính diện tích S tam giác khi vận dụng nhập bài xích tập dượt rõ ràng. Nếu như vẫn tồn tại khó khăn tưởng tượng về kiểu cách thực hiện bài xích hiệu suất cao, các bạn hãy xem thêm một trong những bài xích tập dượt điển hình nổi bật kể từ cơ phiên bản cho tới nâng lên sau đây nhé!
Bài tập dượt 1
Tam giác ABC là tam giác vuông bên trên A, sở hữu độ cao h = 6 centimet. Độ nhiều năm cạnh góc vuông là 8 centimet. Tính diện tích S của tam giác ABC.
Lời giải:
Vì tam giác ABC là tam giác vuông bên trên A, tớ biết cạnh góc vuông có tính nhiều năm 8 centimet và độ cao h = 6 centimet.
Tính diện tích S tam giác (S) bằng phương pháp dùng công thức diện tích S tam giác: S = (1/2) * cạnh góc vuông * độ cao.
S = (1/2) * 8 centimet * 6 centimet = 24 cm²
Vậy diện tích S của tam giác ABC là 24 cm².
Bài tập dượt 3
Tam giác vuông ABC sở hữu cạnh góc vuông AB có tính nhiều năm 10 centimet và diện tích S S = 40 cm². Tính chừng nhiều năm cạnh huyền BC của tam giác vuông ABC.
Lời giải:
Ta biết tam giác vuông ABC sở hữu cạnh góc vuông AB có tính nhiều năm 10 centimet và diện tích S S = 40 cm².
Bước 1: Tính chừng nhiều năm cạnh góc vuông sót lại AC = (S * 2)/ AB = (40 * 2)/10 = 8 cm
Bước 2: Tính chừng nhiều năm cạnh huyền BC của tam giác vuông.Dựa nhập công thức Pytago tớ sở hữu bình phương cạnh huyền bởi vì tổng bình phương 2 cạnh góc vuông
Do cơ (BC)².= (AB)². + (AC)². = 10². + 8². = 164
>> BC = √164 = xấp xỉ 12,9 cm
Bài tập dượt 4
Tam giác ABC có tính nhiều năm tía cạnh là: AB = 6 centimet, BC = 8 centimet và AC = 10 centimet. Tính diện tích S của tam giác ABC.
Lời giải:
Để tính diện tích S tam giác lúc biết chừng nhiều năm tía cạnh, tất cả chúng ta dùng công thức Heron. Công thức này được dùng để làm tính diện tích S của tam giác lúc biết chừng nhiều năm tía cạnh.
Công thức Heron:
Diện tích tam giác ABC (S) = √(p * (p – a) * (p – b) * (p – c))
Trong đó:
a, b và c là chừng nhiều năm tía cạnh của tam giác (trong tình huống này, a = 6 centimet, b = 8 centimet và c = 10 cm).
p là nửa chu vi của tam giác, được xem bởi vì p = (a + b + c) / 2.
Bước 1: Tính nửa chu vi p của tam giác.
p = (6 centimet + 8 centimet + 10 cm) / 2 = 24 centimet / 2 = 12 cm
Bước 2: Tính diện tích S tam giác (S) bởi vì công thức Heron.
S = √(12 centimet * (12 centimet – 6 cm) * (12 centimet – 8 cm) * (12 centimet – 10 cm))
S = √(12 centimet * 6 centimet * 4 centimet * 2 cm) = √(576 cm²) = 24 cm²
Vậy diện tích S của tam giác ABC là 24 cm².
Bài tập dượt 4
Tam giác ABC sở hữu chu vi P.. = 30 centimet và nửa đường kính đàng tròn xoe nội tiếp R = 5 centimet. Tính diện tích S của tam giác ABC.
Lời giải:
Để tính diện tích S tam giác lúc biết chu vi và nửa đường kính đàng tròn xoe nội tiếp, tất cả chúng ta dùng một công thức tương quan cho tới tam giác và đàng tròn xoe nội tiếp.
Cho tam giác ABC sở hữu chu vi P.. và nửa đường kính đàng tròn xoe nội tiếp R, tớ sở hữu những quan hệ sau:
- Diện tích tam giác (S) và nửa đường kính đàng tròn xoe nước ngoài tiếp (R):
S = (P * R) / 2
- Diện tích tam giác (S) và chu vi (P):
S = (P * R) / 2
Trong cơ, P.. là chu vi tam giác và R là nửa đường kính đàng tròn xoe nội tiếp tam giác.
Bước 1: Tính diện tích S tam giác (S) bởi vì công thức diện tích S tam giác và chu vi tam giác.
S = (P * R) / 2 = (30 centimet * 5 cm) / 2 = 150 cm² / 2 = 75 cm²
Vậy diện tích S của tam giác ABC là 75 cm².
Câu căn vặn thông thường gặp
Cách tính diện tích S tam giác lớp 5
Ngay kể từ lớp 5, tất cả chúng ta và đã được học tập phương pháp tính diện tích S tam giác thông thường ABC. Công thức tính diện tích S tam giác lớp 5 cơ là: S(ABC) = ½ (a * h).
Trong cơ, a là chừng nhiều năm của một cạnh nhập tam giác, h là độ cao ứng của cạnh a
Với công thức này, tớ hoàn toàn có thể vận dụng đa số so với những hình tam giác quan trọng như tam giác cân nặng, tam giác đều, tam giác vuông,…
Tính diện tích S tam giác biết 3 cạnh
Cách tính diện tích S tam giác lúc biết chừng nhiều năm 3 cạnh cũng được rằng phía trên. Để tính diện tích S nhập tình huống này, tớ ko thể vận dụng công thức cơ phiên bản như thông thường nữa nhưng mà nên dùng công thức Heron S(ABC) = √(p * (p – a) * (p – b) * (p – c))
Trong cơ, a, b, c là chừng nhiều năm những cạnh tiếp tục mang lại trước, p là chu vi của tam giác được xem theo gót công thức p = a+b+c
Trên đó là toàn cỗ kiến thức và kỹ năng về diện tích tam giác nhưng mà TDS tiếp tục tổ hợp lại. cũng có thể thấy rằng diện tích S hình tam giác có tương đối nhiều công thức tính cực kỳ hoặc và phong phú và đa dạng. Để học tập toán chất lượng rộng lớn, chúng ta nhớ rằng đánh dấu những công thức bên trên và thông thường xuyên thực hiện bài xích tập dượt vận dụng phương pháp tính nhằm đạt thành phẩm cao nhé! Chúc chúng ta sở hữu những giờ học tập toán ăm ắp hào hứng và có lợi.
Xem thêm: Các giải bài toán bằng cách lập phương trình lớp 9 (cực hay, có đáp án).
—-
The Dewey Schools là hệ thống trường quốc tế tuy nhiên ngữ tốt nhất lúc bấy giờ bên trên thủ đô hà nội, tiền phong mang tới nền dạy dỗ chuẩn chỉnh Mỹ và toàn cầu bên trên nước ta. Được xây dựng từ thời điểm năm 2011, đến giờ Dewey Schools tiếp tục sở hữu cho bản thân mình rộng lớn 8000 học viên, 1600 cán cỗ nhân viên cấp dưới, 4 hạ tầng ngôi trường bên trên thủ đô hà nội và Hải Phòng Đất Cảng. Ngoài hạ tầng vật hóa học tiến bộ hàng đầu, Dewey Schools còn ghi điểm nhập đôi mắt bố mẹ bởi vì unique giảng dạy và triết lý dạy dỗ nổi trội gom học viên đã có được hành trang cực tốt nhằm phi vào đời.
Thông tin cậy cơ bản:
- Hotline: 19003293
- Website: https://beyeu.edu.vn/
- Học phí The Dewey Schools
Bình luận