beyeu
beyeu
Trang chủ Giáo Dục Công thức tính diện tích tam giác: vuông, thường, cân, đều

Công thức tính diện tích tam giác: vuông, thường, cân, đều

Công thức tính diện tích S tam giác thông thường, vuông, cân nặng như vậy nào? Mời chúng ta nằm trong tìm hiểu thêm nội dung bài viết tiếp sau đây nhằm tóm được những phương pháp tính diện tích S tam giác dễ nắm bắt và được dùng tối đa nhé.

1. Tính diện tích S tam giác thường

Tam giác ABC đem phụ vương cạnh a, b, c, ha là đàng cao kể từ đỉnh A như hình vẽ:

Bạn đang xem: Công thức tính diện tích tam giác: vuông, thường, cân, đều

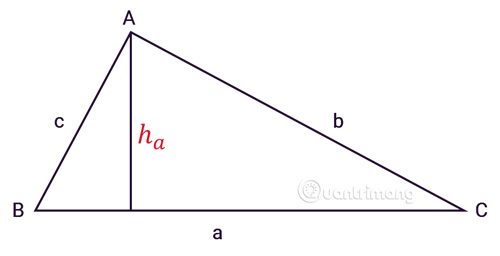
Tính diện tích S tam giác thường

a. Công thức chung

Diện tích tam giác vị độ cao nhân với phỏng lâu năm cạnh đối lập rồi phân tách mang lại 2.

Công thức tính diện tích S tam giác chung

Ví dụ:

Tính diện tích S hình tam giác có tính lâu năm lòng là 5m và độ cao là 24dm.

Giải: Chiều cao 24dm = 2,4m

Diện tích tam giác là:

S=\frac{5\times2.4}{2}=6\ m^2

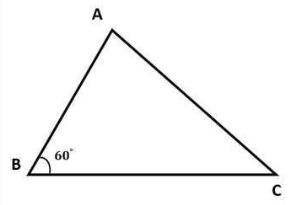
b. Tính diện tích S tam giác lúc biết một góc

Diện tích tam giác vị ½ tích nhị cạnh kề với sin của góc ăn ý vị nhị cạnh cơ nhập tam giác.

Công thức tính diện tích S tam giác lúc biết một góc

Ví dụ:

Tam giác ABC đem cạnh BC = 7, cạnh AB = 5, góc B vị 60 phỏng. Tính diện tích S tam giác ABC?

Giải:

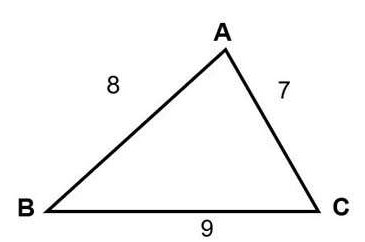
c. Tính diện tích S tam giác lúc biết 3 cạnh vị công thức Heron.

Sử dụng công thức Heron đã và đang được bệnh minh:

Công thức Heron

Với p là nửa chu vi tam giác:

Công thức nửa chu vi tam giác

Có thể viết lách lại vị công thức:

Công thức Heron tính diện tích S tam giác

Ví dụ:

Tính diện tích S hình tam giác có tính lâu năm cạnh AB = 8, AC = 7, CB = 9

Giải:

Nửa chu vi tam giác ABC là

p=\frac{AB\ +\ AC\ +BC}{2}=\frac{8\ +\ 7\ +\ 9}{2}=12

Áp dụng công thức hero tớ có

S\ =\ \sqrt{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}

=\sqrt{12\left(12-8\right)\left(12-7\right)\left(12-9\right)}

=12\sqrt{5}

Tam giác ABC

d. Tính diện tích S vị nửa đường kính đàng tròn trĩnh nước ngoài tiếp tam giác (R).

Lưu ý: Cần cần minh chứng được R là nửa đường kính đàng tròn trĩnh nước ngoài tiếp tam giác.

Ví dụ:

Cho tam giác ABC, phỏng lâu năm những cạnh a = 6, b = 7, c = 5, R = 3 (R là nửa đường kính đàng tròn trĩnh nước ngoài tiếp tam giác ABC). Tính diện tích S của tam giác ABC.

Giải:

S=\frac{abc}{4R}=\ \frac{6\times7\times5}{4\times3\sqrt{2}}=\frac{210}{12\sqrt{2}}=\frac{35\sqrt{2}}{4}

e. Tính diện tích S vị nửa đường kính đàng tròn trĩnh nội tiếp tam giác (r).

Công thức tính diện tích S vị nửa đường kính đàng tròn trĩnh nội tiếp tam giác

  • p: Nửa chu vi tam giác.
  • r: Bán kính đàng tròn trĩnh nội tiếp.

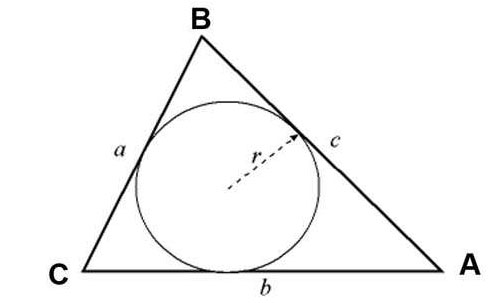
Tính diện tích S vị nửa đường kính đàng tròn trĩnh nội tiếp tam giác

Ví dụ: Tính diện tích S tam giác ABC biết phỏng lâu năm những cạnh AB = đôi mươi, AC = 21, BC = 15, r = 5 (r là nửa đường kính đàng tròn trĩnh nội tiếp tam giác ABC).

Giải:

Nửa chu vi tam giác là:

p=\frac{AB\ +\ AC\ +BC}{2}=\frac{20+21+15}{2}=28

r= 5

Xem thêm: Công thức tính bán kính mặt cầu - Trắc nghiệm mặt cầu có đáp án

Diện tích tam giác là:

S=p\times r=28\times5=140

2. Tính diện tích S tam giác cân

Tam giác cân nặng ABC đem phụ vương cạnh, a là phỏng lâu năm cạnh lòng, b là phỏng lâu năm nhị cạnh mặt mũi, ha là đàng cao kể từ đỉnh A như hình vẽ:

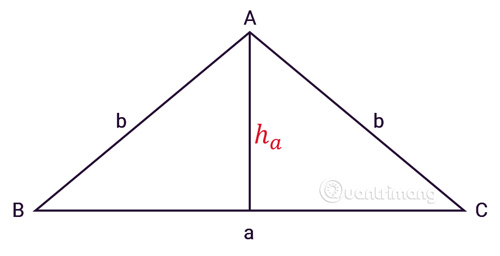
Tính diện tích S tam giác cân

Áp dụng công thức tính diện tích S thông thường, tớ đem công thức tính diện tích S tam giác cân:

Công thức tính diện tích S tam giác cân

3. Tính diện tích tam giác đều

Tam giác đều ABC đem phụ vương cạnh đều nhau, a là phỏng lâu năm những cạnh như hình vẽ:

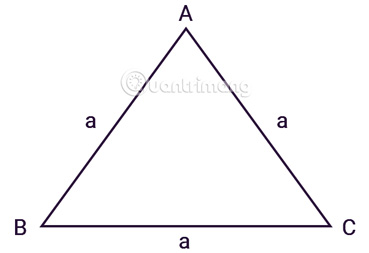
Tính diện tích tam giác đều

Áp dụng tấp tểnh lý Heron nhằm suy rời khỏi, tớ đem công thức tính diện tích tam giác đều:

Công thức tính diện tích tam giác đều

4. Tính diện tích S tam giác vuông

Tam giác ABC vuông bên trên B, a, b là phỏng lâu năm nhị cạnh góc vuông:

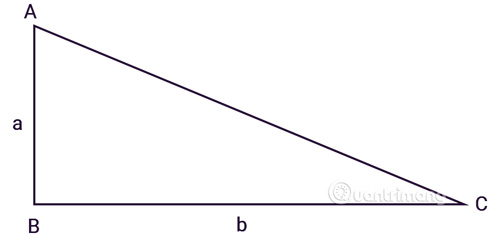
Tính diện tích S tam giác vuông

Áp dụng công thức tính diện tích S thông thường mang lại diện tích S tam giác vuông với độ cao là một nhập 2 cạnh góc vuông và cạnh lòng là cạnh còn sót lại.

Công thức tính diện tích S tam giác vuông:

Công thức tính diện tích S tam giác vuông

5. Tính diện tích S tam giác vuông cân

Tam giác ABC vuông cân nặng bên trên A, a là phỏng lâu năm nhị cạnh góc vuông:

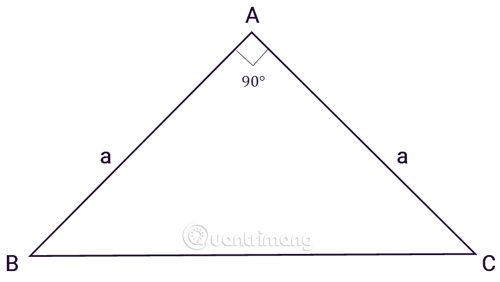
Tính diện tích S tam giác vuông cân

Áp dụng công thức tính diện tích S tam giác vuông mang lại diện tích S tam giác vuông cân nặng với độ cao và cạnh lòng đều nhau, tớ đem công thức:

Tính diện tích S tam giác vuông cân

6. Công thức tính diện tích S tam giác nhập hệ tọa phỏng Oxyz

Về mặt mũi lý thuyết, tớ đều hoàn toàn có thể dử dụng những công thức bên trên nhằm tính diện tích S tam giác nhập không khí hoặc nhập không khí Oxyz. Tuy nhiên vì vậy tiếp tục gặp gỡ một vài trở ngại nhập đo lường và tính toán. Do cơ nhập không khí Oxyz, người tớ thông thường tính diện tích S tam giác bằng phương pháp dùng tích được đặt theo hướng.

Công thức tính diện tích S tam giác nhập hệ tọa phỏng Oxyz

Trong không khí Oxyz, mang lại tam giác ABC. Diện tích tam giác ABC được xem theo đuổi công thức:

S_{\triangle ABC}=\frac{1}{2}|\overrightarrow{AB}\wedge\overrightarrow{AC}|

Ví dụ minh họa:

Trong không khí Oxyz, mang lại tam giác ABC đem tọa phỏng phụ vương đỉnh theo thứ tự là A(-1;1;2), B(1;2;3), C(3;-2;0). Tính diện tích S tam giác ABC.

Bài giải:

Ta có:

\begin{aligned} &\overrightarrow{A B}=(2 ; 1 ; 1) \end{aligned}

\begin{aligned} &\overrightarrow{A C}=(4 ;-3 ;-2) \end{aligned}

S_{\triangle A B C}=\frac{1}{2}|\overrightarrow{A B} \wedge \overrightarrow{A C}|=\frac{\sqrt{165}}{2}

Để tính diện tích S tam giác bạn phải xác lập loại tam giác này là gì, kể từ cơ dò xét ra sức thức tính diện tích S đúng đắn và những nhân tố quan trọng nhằm tính diện tích S tam giác sớm nhất.

Để tính diện tích S tam giác bạn phải xác lập loại tam giác này là gì

Các loại tam giác

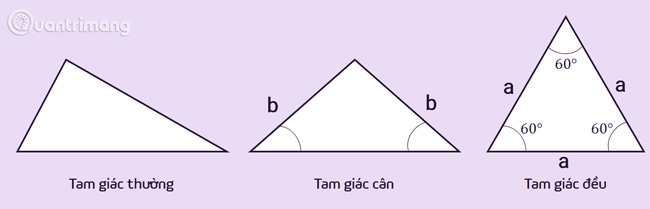
Tam giác thường: là tam giác cơ bạn dạng nhất, có tính lâu năm những cạnh không giống nhau, số đo góc nhập cũng không giống nhau. Tam giác thông thường cũng hoàn toàn có thể bao hàm những tình huống quan trọng của tam giác.

Tam giác cân: là tam giác đem nhị cạnh đều nhau, nhị cạnh này được gọi là nhị cạnh mặt mũi. Đỉnh của một tam giác cân nặng là gửi gắm điểm của nhị cạnh mặt mũi. Góc được tạo nên vị đỉnh được gọi là góc ở đỉnh, nhị góc còn sót lại gọi là góc ở lòng. Tính hóa học của tam giác cân nặng là nhị góc ở lòng thì đều nhau.

Tam giác đều: là tình huống quan trọng của tam giác cân nặng đem cả phụ vương cạnh đều nhau. Tính hóa học của tam giác đều là đem 3 góc đều nhau và vị 60^{\circ}.

Các loại tam giác thông thường, cân nặng, đều

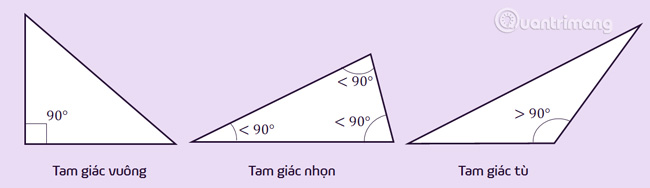
Tam giác vuông: là tam giác mang 1 góc vị 90^{\circ} (là góc vuông).

Tam giác tù: là tam giác mang 1 góc nhập to hơn rộng lớn rộng lớn 90^{\circ}(một góc tù) hoặc mang 1 góc ngoài bé thêm hơn 90^{\circ} (một góc nhọn).

Tam giác nhọn: là tam giác đem phụ vương góc nhập đều nhỏ rộng lớn 90^{\circ} (ba góc nhọn) hoặc đem toàn bộ góc ngoài to hơn 90^{\circ} (sáu góc tù).

Các loại tam giác vuông, nhọn, tù

Xem thêm: Phân giác ngoài của một tam giác là gì?Tính chất đường phân giác của tam giác

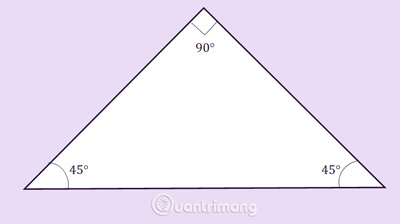
Tam giác vuông cân: vừa vặn là tam giác vuông, vừa vặn là tam giác cân nặng.

Tam giác vuông cân

  • Công thức tính chu vi hình tam giác
  • Công thức tính đàng cao nhập tam giác thông thường, cân nặng, đều, vuông
  • Trọng tâm là gì? Công thức tính trọng tâm của tam giác
  • Đường trung trực là gì?

Trên đấy là tổ hợp những công thức tính diện tích S tam giác phổ biến, tính diện tích S tam giác nhập hệ tọa phỏng oxyz. Nếu đem bất kì do dự, vướng mắc hoặc góp phần, chúng ta hãy nhằm lại comment bên dưới nhằm nằm trong trao thay đổi với Quantrimang.com nhé.

BÀI VIẾT NỔI BẬT

Công thức tính thể tích khối tứ diện

Công thức tính thể tích khối tứ diện là một phần quan trọng của hình học không gian. Khối tứ diện là một loại đa diện mà có bốn mặt phẳng, bốn góc và bốn cạnh. Công thức này rất hữu ích trong nhiều vấn đề liên quan đến lĩnh vực toán học và cơ học. Bài viết sau sẽ cung cấp cho bạn một cái nhìn tổng quan về cách tính toán thể tích của khối tứ diện.

Bài tập phương trình hóa học lớp 8

Bài tập phương trình hóa học lớp 8 được biến soạn có đáp án, hy vọng tài liệu giúp ích cho các bạn học sinh củng cố luyện tập biết cách cân bằng phường trình phản ứng.