Cách viết phương trình tổng quát của đường thẳng lớp 10 cực hay

Bài ghi chép Cách ghi chép phương trình tổng quát của đường thẳng lớp 10 với cách thức giải cụ thể canh ty học viên ôn tập dượt, biết phương pháp thực hiện bài xích tập dượt Cách ghi chép phương trình tổng quát của đường thẳng lớp 10.

A. Phương pháp giải

* Để ghi chép phương trình tổng quát của đường thẳng d tớ cần thiết xác lập :

Bạn đang xem: Cách viết phương trình tổng quát của đường thẳng lớp 10 cực hay

   - Điểm A(x₀; y₀) nằm trong d

   - Một vectơ pháp tuyến n→( a; b) của d

Khi cơ phương trình tổng quát tháo của d là: a(x-x₀) + b(y-y₀) = 0

* Cho đường thẳng liền mạch d: ax+ by+ c= 0 nếu như đường thẳng liền mạch d// ∆ thì đường thẳng liền mạch ∆ sở hữu dạng: ax + by + c’ = 0 (c’ ≠ c) .

B. Ví dụ minh họa

Ví dụ 1: Đường trực tiếp trải qua A(1; -2) , nhận n→ = (1; -2) thực hiện véc tơ pháp tuyến sở hữu phương trình là:

A. x - 2y + 1 = 0.    B. 2x + hắn = 0    C. x - 2y - 5 = 0    D. x - 2y + 5 = 0

Lời giải

Gọi (d) là đường thẳng liền mạch trải qua A và nhận n→ = (1; -2) thực hiện VTPT

=>Phương trình đường thẳng liền mạch (d) : 1(x - 1) - 2(y + 2) = 0 hoặc x - 2y – 5 = 0

Chọn C.

Ví dụ 2: Viết phương trình tổng quát của đường thẳng ∆ trải qua M(1; -3) và nhận vectơ n→(1; 2) thực hiện vectơ pháp tuyến.

A. ∆: x + 2y + 5 = 0    B. ∆: x + 2y – 5 = 0    C. ∆: 2x + hắn + 1 = 0    D. Đáp án khác

Lời giải

Đường trực tiếp ∆: qua loa M( 1; -3) và VTPT n→(1; 2)

Vậy phương trình tổng quát của đường thẳng ∆ là 1(x - 1) + 2(y + 3) = 0

Hay x + 2y + 5 = 0

Chọn A.

Ví dụ 3: Cho đường thẳng liền mạch (d): x-2y + 1= 0 . Nếu đường thẳng liền mạch (∆) trải qua M(1; -1) và tuy nhiên song với d thì ∆ sở hữu phương trình

A. x - 2y - 3 = 0    B. x - 2y + 5 = 0    C. x - 2y +3 = 0    D. x + 2y + 1 = 0

Lời giải

Do đường thẳng liền mạch ∆// d nên đường thẳng liền mạch ∆ sở hữu dạng x - 2y + c = 0 (c ≠ 1)

Ta lại sở hữu M(1; -1) ∈ (∆) ⇒ 1 - 2(-1) + c = 0 ⇔ c = -3

Vậy phương trình ∆: x - 2y - 3 = 0

Chọn A

Ví dụ 4: Cho thân phụ điểm A(1; -2); B(5; -4) và C(-1;4) . Đường cao AA’ của tam giác ABC sở hữu phương trình

A. 3x - 4y + 8 = 0    B. 3x – 4y - 11 = 0    C. -6x + 8y + 11 = 0    D. 8x + 6y + 13 = 0

Lời giải

Ta có BC→ = (-6; 8)

Gọi AA’ là lối cao của tam giác ABC

⇒ AA' nhận VTPT n→ = BC→ = (-6; 8) và qua loa A(1; -2)

Suy đi ra phương trình AA’: -6(x - 1) + 8(y + 2) = 0

Hay -6x + 8y + 22 = 0 ⇔ 3x - 4y - 11 = 0.

Chọn B

Ví dụ 5. Đường trực tiếp d trải qua điểm A( 1; -3) và sở hữu vectơ pháp tuyến n→( 1; 5) sở hữu phương trình tổng quát tháo là:

A. d: x + 5y + 2 = 0    B. d: x- 5y + 2 = 0    C. x + 5y + 14 = 0    D. d: x - 5y + 7 = 0

Lời giải

Ta có: đường thẳng liền mạch d: qua loa A( 1; -3) và VTPT n→( 1; 5)

⇒ Phương trình tổng quát tháo của đường thẳng liền mạch d:

1( x - 1) + 5.(y + 3) = 0 hoặc x + 5y + 14 = 0

Chọn C.

Ví dụ 6. Trong mặt mày bằng phẳng với hệ tọa phỏng Oxy, mang lại tam giác ABC sở hữu A(2; -1); B( 4; 5) và C( -3; 2) . Lập phương trình lối cao của tam giác ABC kẻ kể từ A

A. 7x + 3y – 11 = 0    B. -3x + 7y + 5 = 0    C. 3x + 7y + 2 = 0    D. 7x + 3y + 15 = 0

Lời giải

Gọi H là chân lối vuông góc kẻ kể từ A.

Đường trực tiếp AH : qua loa A( 2;-1) và Nhận VTPT BC→( 7; 3)

⇒ Phương trình lối cao AH :

7( x - 2) + 3(y + 1) = 0 hoặc 7x + 3y – 11 = 0

Chọn A.

Ví dụ 7 : Cho tam giác ABC cân nặng bên trên A sở hữu A(1 ; -2). Gọi M là trung điểm của BC và

M( -2 ; 1). Lập phương trình đường thẳng liền mạch BC ?

A. x + hắn - 3 = 0    B. 2x - hắn + 6 = 0    C. x - hắn + 3 = 0    D. x + hắn + 1 = 0

Lời giải

+ Do tam giác ABC cân nặng bên trên A nên lối trung tuyến AM mặt khác là lối cao

⇒ AM vuông góc BC.

⇒ Đường trực tiếp BC nhận AM→( -3 ; 3) = -3(1 ; -1) thực hiện VTPT

+ Đường trực tiếp BC : qua loa M(-2; 1) và VTPT n→( 1; -1)

⇒ Phương trình đường thẳng liền mạch BC :

1(x + 2) - 1(y - 1) = 0 hoặc x - hắn + 3 = 0

Chọn C.

Ví dụ 8 : Cho tam giác ABC sở hữu lối cao BH : x + hắn - 2 = 0, lối cao CK : 2x + 3y - 5 = 0 và phương trình cạnh BC : 2x - hắn + 2 = 0. Lập phương trình lối cao kẻ kể từ A của tam giác ABC ?

A. x - 3y + 1 = 0    B. x + 4y - 5 = 0    C. x + 2y - 3 =0    D. 2x - hắn + 1 = 0

Lời giải

+ Gọi thân phụ lối cao của tam giác ABC đồng quy bên trên Phường. Tọa phỏng của Phường là nghiệm hệ phương trình :

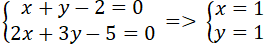 ⇒ P( 1 ; 1)

+Tọa phỏng điểm B là nghiệm hệ phương trình :

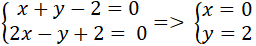 ⇒ B( 0 ;2)

Tương tự động tớ tìm ra tọa phỏng C(-  ;  )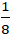

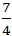+ Đường trực tiếp AP :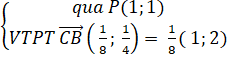 

⇒ Phương trình đường thẳng liền mạch AP :

1(x - 1) + 2(y - 1) = 0 ⇔ x + 2y - 3 = 0

Chọn C.

Ví dụ 9. Phương trình tổng quát tháo của đường thẳng liền mạch d trải qua O và tuy nhiên song với đường thẳng liền mạch ∆ : 3x + 5y - 9 = 0 là:

A. 3x + 5y - 7 = 0    B. 3x + 5y = 0    C. 3x - 5y = 0    D. 3x - 5y + 9 = 0

Lời giải

Do đường thẳng liền mạch d// ∆ nên đường thẳng liền mạch d sở hữu dạng : 3x + 5y + c = 0 ( c ≠ - 9)

Do điểm O(0; 0) nằm trong đường thẳng liền mạch d nên :

3.0 + 5.0 + c = 0 ⇔ c = 0

Vậy phương trình đường thẳng liền mạch d: 3x + 5y = 0

Chọn B.

Ví dụ 10: Cho tam giác ABC sở hữu B(-2; -4). Gọi I và J thứu tự là trung điểm của AB và AC. hiểu đường thẳng liền mạch IJ sở hữu phương trình 2x - 3y + 1 = 0. Lập phương trình đường thẳng liền mạch BC?

A. 2x + 3y - 1 = 0    B. 2x - 3y - 8 = 0    C. 2x + 3y - 6 = 0    D. 2x - 3y + 1 = 0

Lời giải

Do I và J thứu tự là trung điểm của AB và AC nên IJ là lối tầm của tam giác ABC.

⇒ IJ// BC.

⇒ Đường trực tiếp BC sở hữu dạng : 2x - 3y + c = 0 ( c ≠ 1)

Mà điểm B nằm trong BC nên: 2.(-2) - 3(-4) + c = 0 ⇔ c = -8

⇒ phương trình đường thẳng liền mạch BC: 2x - 3y - 8 = 0

Chọn B.

Ví dụ 11. Cho thân phụ đường thẳng liền mạch (a):3x - 2y + 5 = 0; (b): 2x + 4y - 7 = 0 và

Xem thêm: Ca-ta (Qatar) | Hồ sơ - Sự kiện - Nhân chứng

(c): 3x + 4y - 1 = 0 . Phương trình đường thẳng liền mạch d trải qua uỷ thác điểm của a và b , và tuy nhiên song với c là:

A. 24x + 32y - 53 = 0.    B. 23x + 32y + 53 = 0    C. 24x - 33y + 12 = 0.    D. Đáp án khác

Lời giải

Giao điểm của (a) và ( b) nếu như sở hữu là nghiệm hệ phương trình :

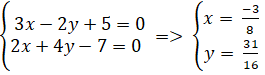 ⇒ A(  ;  )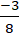

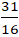Ta sở hữu đường thẳng liền mạch d // c nên đường thẳng liền mạch d sở hữu dạng: 3x+ 4y+ c= 0 (c≠-1)

Vì điểm A nằm trong đường thẳng liền mạch d nên : 3.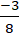 + 4.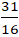 + c = 0 ⇔ c=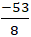 

Vậy d: 3x + 4y + 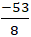 = 0 ⇔ d₃ = 24x + 32y - 53 = 0

Chọn A.

C. Bài tập dượt vận dụng

Câu 1: Lập phương trình đường thẳng liền mạch d trải qua điểm M( 2 ; 1) và nhận vecto n→( -2 ; 1) thực hiện VTPT ?

A. 2x + hắn - 5 = 0    B. - 2x + hắn + 3 = 0    C. 2x - hắn - 4 = 0    D. 2x + hắn - 1 = 0

Lời giải:

Đáp án: B

Đường trực tiếp d :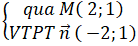 

⇒ Phương trình đường thẳng liền mạch d : - 2(x - 2) + 1(y - 1) = 0

Hay (d) : -2x + hắn + 3 = 0.

Câu 2: Cho đường thẳng liền mạch (a) : 2x+ y- 3=0 và (b) : 3x- 4y+ 1= 0. Lập phương trình đường thẳng liền mạch d trải qua uỷ thác điểm của hai tuyến đường trực tiếp a và b ; nhận vecto n→( 2 ; -3) thực hiện VTPT ?

A. 2x - 3y + 6 = 0    B. -2x - 3y + 6 = 0    C. 2x - 3y + 1 = 0    D. 2x + 3y - 1 =0

Lời giải:

Đáp án: C

+ Giao điểm A của hai tuyến đường trực tiếp a và b là nghiệm hệ phương trình :

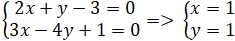 ⇒ A( 1 ; 1)

+ Đường trực tiếp (d) :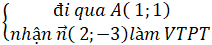 

⇒ Phương trình đường thẳng liền mạch d : 2(x - 1) - 3(y - 1) = 0 hoặc 2x - 3y + 1 = 0.

Câu 3: Trong mặt mày bằng phẳng với hệ tọa phỏng Oxy, mang lại tam giác ABC sở hữu A(2; -1), B(4; 5) và    C( -3; 2) . Lập phương trình lối cao của tam giác ABC kẻ kể từ B

A. 3x - 5y + 1 = 0    B. 3x + 5y - trăng tròn = 0    C. 3x + 5y - 12 = 0    D. 5x - 3y -5 = 0

Lời giải:

Đáp án: D

Gọi H là chân lối vuông góc kẻ kể từ B của tam giác ABC.

Đường trực tiếp BH :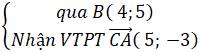 

⇒ Phương trình lối cao BH :

5(x - 4) – 3(y - 5) = 0 hoặc 5x - 3y – 5 = 0

Câu 4: Trong mặt mày bằng phẳng với hệ tọa phỏng Oxy, mang lại tam giác ABC sở hữu A(2;-1) ; B( 4;5) và   C( -3; 2). Tìm trực tâm tam giác ABC?

A. ( 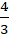 ; -  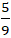)    B. (  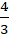;  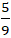)    C. (  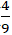;  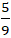)    D. (  ;  )

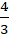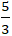Lời giải:

Đáp án: B

+ Gọi H và K thứu tự là chân lối vuông góc kẻ kể từ C và B của tam giác ABC.

+ Đường trực tiếp CH :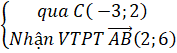 

⇒ Phương trình lối cao CH :

2(x + 3) + 6(y - 2) = 0 hoặc 2x + 6y – 6 = 0

⇔ (CH) : x+ 3y – 3= 0

+ Đường trực tiếp BK :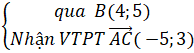 

=>Phương trình lối cao BK : - 5(x - 4) + 3(y - 5)=0 hoặc -5x + 3y + 5 = 0.

+ Gọi Phường là trực tâm tam giác ABC. Khi cơ Phường là uỷ thác điểm của hai tuyến đường cao CH và BK nên tọa phỏng điểm Phường là nghiệm hệ :

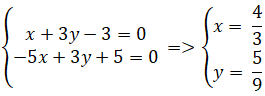
Vậy trực tâm tam giác ABC là P(  ;  )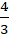

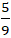Câu 5: Cho tam giác ABC sở hữu A( 2;-1) ; B( 4; 5) và C( -3; 2). Phương trình tổng quát tháo của lối cao AH của tam giác ABC là:

A. 3x - 7y + 11 = 0.    B. 7x + 3y - 11 = 0    C. 3x - 7y - 13 = 0.    D. 7x + 3y + 13 = 0.

Lời giải:

Đáp án: B

Gọi AH là lối cao của tam giác.

Đường trực tiếp AH : trải qua A( 2; -1) và nhận BC→ = (-7; -3) = - (7; 3) thực hiện VTPT

=> Phương trình tổng quát tháo AH: 7(x - 2) + 3(y + 1)= 0 hoặc 7x + 3y - 11 = 0

Câu 6: Cho đường thẳng liền mạch (d): 3x- 2y+ 8= 0. Đường trực tiếp ∆ trải qua M(3; 1) và tuy nhiên song với (d) sở hữu phương trình:

A. 3x - 2y - 7 = 0.    B. 2x + 3y - 9 = 0.    C. 2x - 3y - 3 = 0.    D. 3x - 2y + 1 = 0

Lời giải:

Đáp án: A

Do ∆ tuy nhiên song với d nên sở hữu phương trình dạng: 3x - 2y + c = 0 (c ≠ 8)

Mà ∆ trải qua M (3;1) nên 3.3 - 2.1 + c = 0 nên c = - 7

Vậy phương trình ∆: 3x - 2y - 7 = 0

Câu 7: Cho tam giác ABC sở hữu B(2; -3). Gọi I và J thứu tự là trung điểm của AB và AC. hiểu đường thẳng liền mạch IJ sở hữu phương trình x- y+ 3= 0. Lập phương trình đường thẳng liền mạch BC?

A. x + hắn + 2 = 0    B. x - hắn - 5 = 0    C. x - hắn + 6 = 0    D. x - hắn = 0

Lời giải:

Đáp án: B

Do I và J thứu tự là trung điểm của AB và AC nên IJ là lối tầm của tam giác ABC.

⇒ IJ// BC.

⇒ Đường trực tiếp BC sở hữu dạng : x - hắn + c = 0 ( c ≠ 3)

Mà điểm B nằm trong BC nên: 2 - (-3) + c = 0 ⇔ c = -5

⇒ phương trình đường thẳng liền mạch BC: x - hắn - 5 = 0

Câu 8: Cho tam giác ABC cân nặng bên trên A sở hữu A(3 ; 2). Gọi M là trung điểm của BC và          M( -2 ; -4). Lập phương trình đường thẳng liền mạch BC ?

A. 6x - 5y + 13 = 0    B. 5x - 6y + 6 = 0    C. 5x + 6y + 34 = 0    D. 5x + 6y + 1 = 0

Lời giải:

Đáp án: C

+ Do tam giác ABC cân nặng bên trên A nên lối trung tuyến AM mặt khác là lối cao

⇒ AM vuông góc BC.

⇒ Đường trực tiếp BC nhận AM→( - 5; -6) = -(5; 6) thực hiện VTPT

+ Đường trực tiếp BC :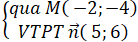 

⇒ Phương trình đường thẳng liền mạch BC :

5(x + 2) + 6( hắn + 4) = 0 hoặc 5x + 6y + 34= 0

Câu 9: Viết phương trình tổng quát của đường thẳng d trải qua điểm M( -1; 2) và tuy nhiên song với trục Ox.

A. hắn + 2 = 0    B. x + 1 = 0    C. x - 1 = 0    D. hắn - 2 = 0

Lời giải:

Đáp án: D

Trục Ox sở hữu phương trình y= 0

Đường trực tiếp d tuy nhiên song với trục Ox sở hữu dạng : hắn + c = 0 ( c ≠ 0)

Vì đường thẳng liền mạch d trải qua điểm M( -1 ;2) nên 2 + c = 0 ⇔ c= -2

Vậy phương trình đường thẳng liền mạch d cần thiết lần là : hắn - 2= 0

D. Mọi người cũng hỏi

Phương trình tổng quát tháo là gì?

Trả lời: Phương trình tổng quát tháo là 1 trong những phương trình đại số chứa chấp những đổi thay số và thông số ko rõ ràng. Nó thể hiện nay quan hệ trong số những đổi thay số nhưng mà ko thể hiện độ quý hiếm rõ ràng của bọn chúng.

Xem thêm: Top 200+ hình nền Rồng cho điện thoại và máy tính: Mang đến may mắn và tài lộc

Cách ghi chép phương trình tổng quát tháo như vậy nào?

Trả lời: Để ghi chép phương trình tổng quát tháo, tớ dùng những ký hiệu đổi thay x, hắn, z,... và những thông số a, b, c,... nhưng mà không chỉ có định vị trị rõ ràng. Ví dụ: ax + by = c là phương trình tổng quát tháo của một đường thẳng liền mạch.

Phương trình tổng quát tháo được dùng vô nghành nghề nào?

Trả lời: Phương trình tổng quát tháo được dùng rộng thoải mái vô đại số và hình học tập, canh ty quy mô hóa những mối liên hệ toán học tập phức tạp, tạo nên ĐK mang lại việc giải những câu hỏi và phân tách những quy mô trong vô số nhiều nghành nghề khoa học tập và nghệ thuật.

Phương trình tổng quát tháo và phương trình format giản dị và đơn giản không giống nhau như vậy nào?

Trả lời: Phương trình tổng quát tháo ko thể hiện độ quý hiếm rõ ràng của đổi thay số, trong những lúc phương trình format giản dị và đơn giản là phương trình đã và đang được giải quyết và xử lý nhằm lần đi ra độ quý hiếm rõ ràng của đổi thay số. Phương trình tổng quát tháo thể hiện nay một quan hệ tổng quát tháo, trong những lúc phương trình format giản dị và đơn giản mang lại tớ thành quả rõ ràng sau khoản thời gian tiến hành những phép tắc tính.