beyeu
beyeu
Trang chủ Giáo Dục Phương pháp giải nhanh bất phương trình bậc 2 - Toán 10

Phương pháp giải nhanh bất phương trình bậc 2 - Toán 10

Bất phương trình bậc 2 là 1 trong trong mỗi dạng toán khó khăn nằm trong công tác Toán lớp 10 vì như thế tính đa dạng và phong phú và kết hợp nhiều cách thức giải của chính nó. Trong nội dung bài viết tiếp sau đây, VUIHOC tiếp tục với những em học viên ôn tập dượt lý thuyết và tìm hiểu thêm những dạng bài xích tập dượt bất phương trình bậc 2 điển hình nổi bật.

1. Tổng ôn lý thuyết bất phương trình bậc 2

1.1. Định nghĩa bất phương trình bậc 2

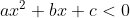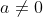
Bất phương trình bậc 2 ẩn x sở hữu dạng tổng quát lác là ax^2+bx+c<0 (hoặc ax^2+bx+c\leq 0$, $ax^2+bx+c>0$, $ax^2+bx+c\geq 0), vô tê liệt a,b,c là những số thực cho tới trước, a\neq 0

Bạn đang xem: Phương pháp giải nhanh bất phương trình bậc 2 - Toán 10

Ví dụ về bất phương trình bậc 2: x^2-2>0, 2x^2+3x-5>0,...
 

Giải bất phương trình bậc 2 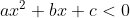ax^2+bx+c<0 thực ra đó là quy trình lần những khoảng chừng thoả mãn f(x)=ax^2+bx+c nằm trong vết với a (a<0) hoặc trái ngược vết với a (a>0).

1.2. Tam thức bậc nhì - vết của tam thức bậc hai

Ta sở hữu toan lý về vết của tam thức bậc nhì như sau: 

Cho f(x)=ax^2+bx+c, =b^2-4ac

Bảng xét vết của tam thức bậc 2:

bảng xét vết tam thức bậc nhì bất phương trình bậc 2

Nhận xét:

ax^{2} + bx +c > 0, \forall R \Leftrightarrow \left\{\begin{matrix} a > 0\\ \Delta < 0 \end{matrix}\right.

ax^{2} + bx +c < 0, \forall R \Leftrightarrow \left\{\begin{matrix} a < 0\\ \Delta < 0 \end{matrix}\right.

Đăng ký tức thì và để được những thầy cô ôn tập dượt và thiết kế trong suốt lộ trình học tập tập THPT vững vàng vàng

2. Các dạng bài xích tập dượt giải bất phương trình bậc 2 lớp 10

Trong công tác Đại số lớp 10 khi tham gia học về bất phương trình bậc 2, VUIHOC tổ hợp được 5 dạng bài xích tập dượt điển hình nổi bật thông thường bắt gặp nhất. Các em học viên nắm rõ 5 dạng cơ bạn dạng này tiếp tục rất có thể giải đa số toàn bộ những bài xích tập dượt bất phương trình bậc 2 vô công tác học tập hoặc trong số đề đánh giá.

2.1. Dạng 1: Giải bất phương trình bậc 2 lớp 10

Phương pháp:

  • Bước 1: Biến thay đổi bất phương trình bậc 2 về dạng một vế vì như thế 0, một vế là tam thức bậc 2.

  • Bước 2: Xét vết vế trái ngược tam thức bậc nhì và Kết luận.

Ví dụ 1 (bài 3 trang 105 SGK đại số 10): Giải những bất phương trình sau đây:

a) 4x^2-x+1<0

b) -3x^2+x+40

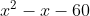
c) x^2-x-60

Hướng dẫn giải:

a) 4x^2 - x+1<0

– Xét tam thức f(x) = 4x^2 - x + 1

– Ta có: Δ= -15 < 0; a = 4 > 0 nên f(x) > 0 ∀x ∈ R

⇒ Bất phương trình tiếp tục cho tới vô nghiệm.

b) -3x^2 + x + 4 \geq 0

– Xét tam thức f(x) = -3x^2 + x + 4

– Ta sở hữu : Δ = 1 + 48 = 49 > 0 sở hữu nhì nghiệm phân biệt là: x = -1 và x = 4/3, thông số a = -3 < 0.

⇒  f(x) ≥ 0 Lúc -1 ≤ x ≤ 4/3. (Trong trái ngược vết với a, ngoài nằm trong vết với a)

⇒ Tập nghiệm của bất phương trình là: S = [-1; 4/3]

c) 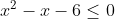x^2 - x - 6 \leq 0

– Xét tam thức 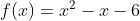f(x)=x^2 - x - 6 sở hữu nhì nghiệm x = -2 và x = 3, thông số a = 1 > 0

⇒ f(x) ≤ 0 vừa lòng Lúc -2 ≤ x ≤ 3.

⇒ Tập nghiệm của bất phương trình là: S = [-2; 3].

Ví dụ 2 (trang 145 sgk Đại số 10 nâng cao): Giải những bất phương trình bậc 2 sau:

a) -5x^2 + 4x + 12 < 0

b) 16x^2 + 40x +25 < 0

c) 3x^2 - 4x+4 \geq 0

Hướng dẫn giải:

a) Tam thức bậc nhì -5x2 + 4x + 12 sở hữu 2 nghiệm thứu tự là 2 và 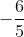-\frac{6}{5} và sở hữu thông số a = -5 < 0 nên

-5x^{2} + 4x + 12 < 0

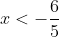\Leftrightarrow x < -\frac{6}{5} hoặc x > 2

Vậy tập dượt nghiệm của bất phương trình tiếp tục cho tới là:

S = (-\infty ; -\frac{6}{5}) \cup (2; +\infty )

b)Tam thức 16x^2 +40x + 25 có:

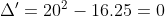\Delta ' = 20^2 - 16.25 = 0 và thông số a = 16 > 0

Do đó; 16x^2 +40x + 25 ≥ 0; ∀ x ∈ R

Suy đi ra, bất phương trình bậc 2 16x^2 +40x + 25 < 0 vô nghiệm

Vậy S = ∅

c)Tam thức 3x^{2} - 4x +4 sở hữu ∆’ = (-2)2 – 4.3 = -10 < 0

Hệ số a= 3 > 0

Do tê liệt, 3x^2 - 4x +4 \geq 0; \forall x \in \mathbb{R}

Vậy tập dượt nghiệm của bất phương trình bậc 2 tiếp tục cho rằng S = 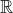\mathbb{R}.

Tham khảo tức thì cuốn sách ôn thi đua trung học phổ thông tổ hợp kỹ năng cách thức giải từng dạng bài xích tập dượt Toán

2.2. Dạng 2: Cách giải bất phương trình bậc 2 dạng tích

Phương pháp:

  • Bước 1: Biến thay đổi bất phương trình bậc 2 về dạng tích và thương những nhị thức hàng đầu và tam thức bậc nhì.

  • Bước 2: Xét vết những nhị thức hàng đầu và tam thức bậc 2 tiếp tục biến hóa bên trên và Kết luận nghiệm giải đi ra được.

Ví dụ 1: Giải những bất phương trình bậc 2 dạng tích sau đây:

a) 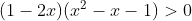(1 - 2x)(x^{2} - x - 1) > 0

b) x^{4} - 5x^{2} + 2x + 3 \leq 0

Hướng dẫn giải:

a) Lập bảng xét dấu:

Bảng xét vết bất phương trình bậc 2 dạng tích

Dựa vô bảng xét vết bên trên, tao sở hữu tập dượt nghiệm của bất phương trình bậc 2 dạng tích đề bài xích là:

S = (-\infty ; \frac{1 - \sqrt{5}}{2}) \cup (\frac{1}{2}; \frac{1 + \sqrt{5}}{2})

b) Bất phương trình tương tự sở hữu dạng:

(x^{4} - 4x^{2} + 4) - (x^{2} - 2x + 1) \leq 0

\Leftrightarrow (x^{2} -2)^{2} - (x - 1)^{2} \leq 0 \Leftrightarrow (x^{2} + x - 3)(x^{2} - x - 1) \leq 0

Ta sở hữu bảng xét vết sau:

Bảng xét vết bất phương trình bậc 2 dạng phương trình tích

Dựa vô bảng xét vết bên trên, tao sở hữu tập dượt nghiệm bất phương trình bậc 2 tiếp tục cho tới là:

S = \left [\frac{-1 - \sqrt{13}}{2}; \frac{1 - \sqrt{5}}{2} \right ] \cup \left [\frac{-1 + \sqrt{13}}{2}; \frac{1 + \sqrt{5}}{2} \right ]

Ví dụ 2: Tìm m nhằm bất phương trình bậc 2 tại đây sở hữu nghiệm:

\sqrt{x - m^{2} - m} (3 - \frac{x + 1}{x^{3} - x^{2} - 3x + 3}) < 0

Hướng dẫn giải:

Ta có:

\sqrt{x - m^{2} - m} (3 - \frac{x + 1}{x^{3} - x^{2} - 3x + 3}) < 0

\Leftrightarrow \left\{\begin{matrix} 3 - \frac{x + 1}{x^{3} - x^{2} - 3x + 3} < 0\\ x > m^{2} + m \end{matrix}\right.

\Leftrightarrow \left\{\begin{matrix} \frac{(x - 2)(3x^{2} + 3x - 4)}{(x - 1)(x^{2} - 3)}\\x > m^{2} + m \end{matrix}\right. < 0

Bảng xét dấu:

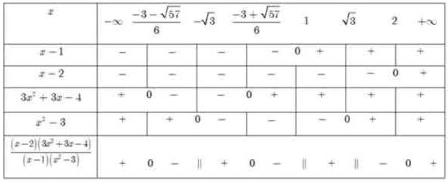
Bảng xét vết bất phương trình bậc 2 dạng lần thông số m

Tập nghiệm của bất phương trình bậc 2 đề bài xích là:

S = \left ( \frac{-3 - \sqrt{57}}{6}; -\sqrt{3} \right ) \cup \left ( \frac{-3 + \sqrt{57}}{6}; 1 \right ) \cup (\sqrt{3}; 2)

Do tê liệt, bất phương trình bậc 2 tiếp tục sở hữu đem nghiệm Lúc và chỉ khi: 

m^2+m<2 \Rightarrow m^2+m-2<0 \Rightarrow -2<m<1

Kết luận:  -2 < m < 1

2.3. Dạng 3: Giải bất phương trình chứa chấp ẩn ở mẫu

Phương pháp:

  • Bước 1: Biến thay đổi giải bất phương trình bậc 2 lớp 10 về dạng tích và thương những nhị thức hàng đầu và tam thức bậc nhì.

  • Bước 2: Xét vết của những nhị thức hàng đầu và tam thức bậc 2 phía trên, Kết luận nghiệm

Lưu ý: Cần chú ý cho tới những ĐK xác lập của bất phương trình Lúc giải bất phương trình bậc 2 sở hữu ẩn ở kiểu.

Ví dụ 1 (trang 145 sgk Đại số 10 nâng cao): Giải những bất phương trình bậc 2 sau đây:

a) \frac{x^{2} - 9x + 14}{x^{2} - 5x + 4} > 0

b) \frac{-2x^{2} +7x + 7}{x^{2} - 3x - 10} \leq -1

Hướng dẫn giải:

a)Ta có:

x2 - 9x + 14 = 0

\Leftrightarrow x = 2 hoặc x = 7

Xem thêm: Công thức làm sữa hạt bằng máy cực nhanh

và x2 - 5x + 4 = 0

\Leftrightarrow x = 1 hoặc x = 4

Ta sở hữu bảng xét dấu:

bảng xét vết bất phương trình bậc 2 chứa chấp ẩn ở kiểu ví dụ 1
Do tê liệt, tập dượt nghiệm của bất phương trình bậc 2 là: S = (-∞; 1) ∪ (7; + ∞)

b)Ta có:

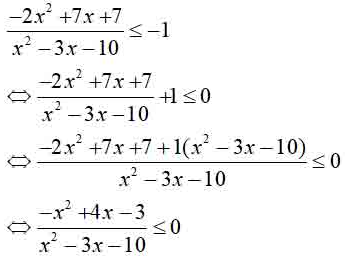
Giải bất phương trình bậc 2 chứa chấp ẩn ở kiểu ví dụ 1

Lại có: -x^2+4x-3 = 0 \Rightarrow x=1; x=3

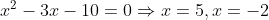
Và: x^2-3x-10=0 \Rightarrow x=5, x=-2

Ta sở hữu bảng xét vết sau đây:

Bảng xét vết bất phương trình bậc 2 chứa chấp ẩn ở kiểu ví dụ 1

Do tê liệt, tập dượt nghiệm của bất phương trình bậc 2 tiếp tục cho tới là: S = (-∞; -2) ∪ [1;3] ∪ (5; +∞)

Ví dụ 2: Giải những bất phương trình bậc 2 sau:

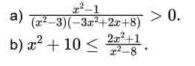
Giải bất phương trình bậc 2 chứa chấp ẩn ở kiểu ví dụ 2

Hướng dẫn giải:

a)Bảng xét vết sở hữu dạng:

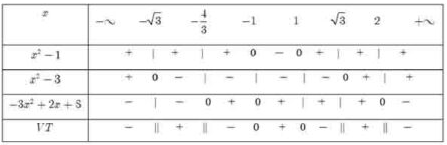
Bảng xét vết bất phương trình bậc 2 chứa chấp ẩn ở kiểu ví dụ 2

Dựa vô bảng xét vết, tao sở hữu tập dượt nghiệm bất phương trình bậc 2 tiếp tục cho tới là:

Tập phù hợp nghiệm bất phương trình bậc 2 chứa chấp ẩn ở kiểu ví dụ 2

Hướng dẫn giải bất phương trình bậc 2 chứa chấp ẩn ở kiểu ví dụ 2

Ta sở hữu bảng xét dấu:

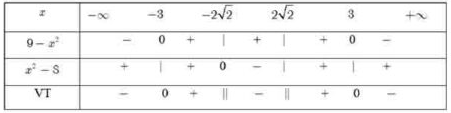
Bảng xét vết giải bất phương trình bậc 2 chứa chấp ẩn ở kiểu ví dụ 2

Dựa vô bảng xét vết bên trên, tao sở hữu tập dượt nghiệm của bất phương trình bậc 2 đề bài xích là: 

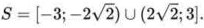
Tập phù hợp nghiệm giải bất phương trình bậc 2 chứa chấp ẩn ở kiểu ví dụ 2

2.4. Dạng 4: Tìm ĐK của thông số nhằm bất phương trình vô nghiệm – sở hữu nghiệm – nghiệm đúng

Phương pháp giải: 

Ta dùng một trong những đặc thù sau:

  • Nếu 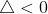\triangle <0 thì tam thức bậc 2 tiếp tục nằm trong vết với a.

  • Bình phương, độ quý hiếm vô cùng, căn bậc 2 của biểu thức luôn luôn ko khi nào âm.

Ví dụ 1 (Bài 4 trang 105 SGK Đại số 10): Tìm những độ quý hiếm thông số m nhằm phương trình tại đây vô nghiệm:

a)(m - 2)x^2 + 2(2m - 3)x + 5m - 6 = 0

b)(3 - m)x^2 - 2(m + 3)x + m + 2 = 0


Hướng dẫn giải:

a)(m - 2)x^2 + 2(2m - 3)x + 5m - 6 = 0 (*)

• Nếu m – 2 = 0 ⇔ m = 2, Lúc tê liệt phương trình (*) biến hóa thành:

 2x + 4 = 0 ⇔ x = -2 => phương trình (*) sở hữu một nghiệm

⇒ m = 2 ko nên là độ quý hiếm cần thiết lần.

• Nếu m – 2 ≠ 0 ⇔ m ≠ 2 tao có:

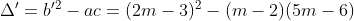
\Delta ' = b'^2 - ac = (2m - 3)^2 - (m - 2)(5m - 6)

= 4m^2 - 12m + 9 - 5m^2 + 6m + 10m - 12

= -m^2 + 4m - 3 = (-m + 3)(m - 1)

Ta thấy (*) vô nghiệm ⇔ Δ’ < 0 ⇔ (-m + 3)(m – 1) < 0 ⇔ m ∈ (-∞; 1) ∪ (3; +∞)

Vậy với m ∈ (-∞; 1) ∪ (3; +∞) thì phương trình vô nghiệm.

b) (3 - m)x^2 - 2(m + 3)x + m + 2 = 0 (*)

• Nếu 3 – m = 0 ⇔ m = 3 Lúc tê liệt (*) biến hóa thành:

-6x + 5 = 0 ⇔ x = ⅚ ⇒ m = 3 ko nên là độ quý hiếm cần thiết lần.

• Nếu 3 – m ≠ 0 ⇔ m ≠ 3 tao có:

\Delta ' = b' - ac = (m + 3)^2 - (3 - m)(m + 2)

= m^2 + 6m + 9 - 3m - 6 + m^2 + 2m

= 2m^2 + 5m + 3 = (m + 1)(2m + 3)

Ta thấy (*) vô nghiệm ⇔ Δ’ < 0 ⇔ (m + 1)(2m + 3) < 0 ⇔ m ∈ (-3/2; -1)

Vậy với m ∈ (-3/2; -1) thì phương trình vô nghiệm.

Ví dụ 2 (Trang 145 sgk Đại số lớp 10 nâng cao): Tìm những độ quý hiếm thông số m nhằm từng phương trình tại đây sở hữu nghiệm:

a) (m-5)x^2-4mx+m-2=0

b) (m+1)x^2+2(m-1)x+2m-3=0

Hướng dẫn giải:

a)(m-5)x^2-4mx+m-2=0

+ Khi m – 5 = 0 ⇒ m=5 phương trình trở thành:

-20x + 3 = 0⇒x = 3/20

+ Khi m – 5 ≠ 0⇒m ≠ 5, phương trình sở hữu nghiệm Lúc và chỉ khi:

Δ’ =(-2m)^2– (m – 2)( m – 5)≥0

⇒ 4m^2-(m^2-5m-2m+10) \geq 0 ⇒ 4m^2-m^2+7m-10 \geq 0

\Rightarrow 3m^{2} + 7m - 10 \geq 0 \Rightarrow \left\{\begin{matrix} m \geq 1\\ m \leq -\frac{10}{3} \end{matrix}\right.

Kết phù hợp 2 tình huống bên trên, tao sở hữu tụ họp những độ quý hiếm m nhằm phương trình sở hữu nghiệm là:

m \in (-\infty ; \frac{10}{3}] \cup [1; +\infty )

b) (m+1)x^2+2(m-1)x+2m-3=0

  • Khi m=-1 thì phương trình tiếp tục cho tới trở thành:

0.x2 + 2(-1-1)x + 2.(-1) - 3 = 0

Hay -4x-5=0 Lúc và chỉ Lúc x=-5/4

Do tê liệt, m=-1 thoả mãn đề bài xích.

  • Khi m\neq -1, phương trình đề bài xích sở hữu m nghiệm Lúc và chỉ khi:

\Delta ' = (m - 1)^{2} - (m + 1)(2m - 3) \geq 0

\Leftrightarrow m^{2} - 2m + 1 - (2m^{2} - 3m + 2m -3) \geq 0

\Leftrightarrow -m^{2} - m + 4 \geq 0

\Leftrightarrow \frac{-1 - \sqrt{17}}{2} \leq m \leq \frac{-1 + \sqrt{17}}{2}

Kết phù hợp cả hai tình huống vậy những độ quý hiếm của m vừa lòng đề bài xích lại:

m \in \left [ \frac{-1 - \sqrt{17}}{2}; \frac{-1 + \sqrt{17}}{2} \right ]

2.5. Dạng 5: Giải hệ bất phương trình bậc 2

Phương pháp giải:

  • Bước 1: Giải từng bất phương trình bậc 2 sở hữu vô hệ.

  • Bước 2: Kết phù hợp nghiệm, tiếp sau đó Kết luận nghiệm.
     

Ví dụ (Trang 145 sgk Đại số 10 nâng cao): Giải những hệ bất phương trình bậc 2 sau:

a) \left\{\begin{matrix} 2x^{2} + 9x + 7 > 0\\ x^{2} + x - 6 < 0 \end{matrix}\right.

b) \left\{\begin{matrix} 4x^{2} - 5x - 6 \leq 0\\ -4x^{2} + 12x - 5 < 0 \end{matrix}\right.

c) \left\{\begin{matrix} -2x^{2} - 5x + 4 \leq 0\\ -x^{2} - 3x + 10 \geq 0 \end{matrix}\right.

d) \left\{\begin{matrix} 2x^{2} + x - 6 > 0\\ 3x^{2} - 10x + 3 > 0 \end{matrix}\right.

Hướng dẫn giải:

Hướng dẫn giải ví dụ giải hệ bất phương trình bậc 2

Hướng dẫn giải ví dụ giải hệ bất phương trình bậc 2 phần b

Hướng dẫn giải ví dụ giải hệ bất phương trình bậc 2 phần c

Hướng dẫn giải ví dụ giải hệ bất phương trình bậc 2 phần d

PAS VUIHOC – GIẢI PHÁP ÔN LUYỆN CÁ NHÂN HÓA

Khóa học tập online ĐẦU TIÊN VÀ DUY NHẤT:  

⭐ Xây dựng trong suốt lộ trình học tập kể từ rơi rụng gốc cho tới 27+  

⭐ Chọn thầy cô, lớp, môn học tập theo dõi sở thích  

⭐ Tương tác thẳng hai phía nằm trong thầy cô  

⭐ Học tới trường lại cho tới lúc nào hiểu bài xích thì thôi

⭐ Rèn tips tricks canh ty bức tốc thời hạn thực hiện đề

⭐ Tặng full cỗ tư liệu độc quyền vô quy trình học tập tập

Xem thêm: Phân giác ngoài của một tam giác là gì?Tính chất đường phân giác của tam giác

Đăng ký học tập demo không tính phí ngay!!


Các em tiếp tục nằm trong VUIHOC ôn tập dượt tổng quan liêu lý thuyết bất phương trình bậc 2 tất nhiên những dạng bài xích tập dượt bất phương trình bậc 2 điển hình nổi bật, thông thường xuất hiện nay vô công tác Toán lớp 10 và những đề đánh giá, đề thi đua trung học phổ thông Quốc gia. Để học tập nhiều hơn thế những kỹ năng Toán trung học phổ thông hữu dụng, những em truy vấn trang web ngôi trường học tập online beyeu.edu.vn hoặc ĐK khoá học tập tức thì bên trên phía trên nhé!

BÀI VIẾT NỔI BẬT

Giải bài tập SGK Sinh học lớp 9 đầy đủ và hay nhất

Giải bài tập SGK Sinh học lớp 9 là tài liệu tổng hợp đầy đủ các kiến thức trọng tâm những bài tập củng cố kiến thức về Sinh học Di Truyền Và Biến Dị, Sinh Vật Và Môi Trường. Để giúp các em nâng cao hiệu quả học tập, tiết kiệm thời gian làm bài, eLib đã tổng hợp các bài tập SGK Sinh học 9 bao gồm phương pháp giải nhanh chóng và hướng dẫn giải rõ ràng cho từng bài tập. Mời các em cùng tham khảo!