
Tiếp tục với những mục chính hình học tập Toán lớp 9, nội dung bài viết thời điểm ngày hôm nay tất cả chúng ta tiếp tục bên nhau thám thính hiểu về mục chính Đường tròn xoe nước ngoài tiếp. Đường tròn xoe nội tiếp. Nội dung của nội dung bài viết này bao hàm phần tóm lược lý thuyết cần thiết tóm và phần giải bài xích tập dượt trải qua những đề trắc nghiệm và tự động luận. Nào tất cả chúng ta nằm trong chính thức nhé!
Bài ghi chép xem thêm thêm:
Bạn đang xem: Đường tròn ngoại tiếp. Đường tròn nội tiếp - HOCMAI
- Vị trí kha khá của hai tuyến phố tròn
- Sự xác lập đàng tròn xoe. Tính hóa học đối xứng của đàng tròn
I. Lý thuyết cần thiết tóm về Đường tròn xoe nước ngoài tiếp – Đường tròn xoe nội tiếp
1. Đường tròn xoe nước ngoài tiếp
a) Định nghĩa
Đường tròn xoe trải qua toàn bộ những đỉnh của một nhiều giác được gọi là đàng tròn xoe nước ngoài tiếp đa
giác và nhiều giác được gọi là nhiều giác nội tiếp đàng tròn xoe.
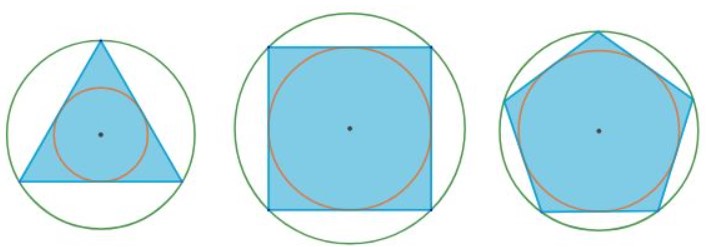
Ví dụ: Trong những hình tiếp sau đây, đàng tròn xoe tâm O được gọi là đàng tròn xoe nước ngoài tiếp nhiều giác vì thế nó trải qua toàn bộ những đỉnh của nhiều giác.
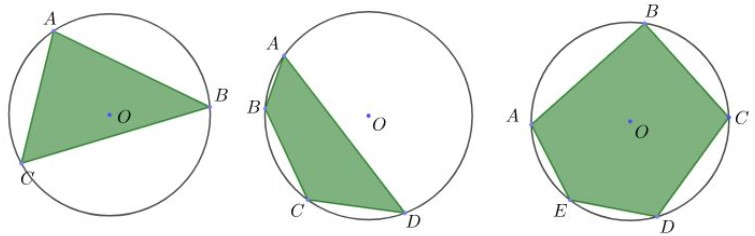
Khi tê liệt, ΔABC, tứ giác CBAD và ngũ giác ABCDE theo thứ tự được gọi là tam giác nội tiếp, tứ giác nội tiếp và ngũ giác nội tiếp đàng tròn xoe (Đa giác ở bên phía trong đàng tròn).
b) Cách xác lập tâm đàng tròn xoe nước ngoài tiếp nhiều giác
Tâm đàng tròn xoe nước ngoài tiếp nhiều giác là phú điểm của những đàng trung trực của toàn bộ những cạnh.
Vậy nên, nhằm xác lập được tâm đàng tròn xoe nước ngoài tiếp một nhiều giác, tớ cần thiết thực hiện như sau:
- Kẻ những đàng trung trực của những cạnh tiếp sau đó xác lập phú điểm.
- Vẽ đàng tròn xoe sở hữu tâm là phú điểm của những đàng trung trực và nửa đường kính đó là khoảng cách tính kể từ phú điểm đến chọn lựa những đỉnh.
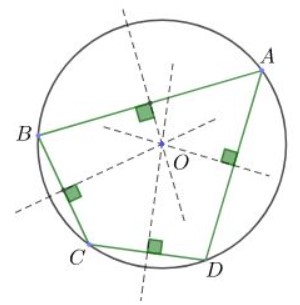
Vì vậy, một nhiều giác sẽ sở hữu được đàng tròn xoe nước ngoài tiếp nếu như đàng trung trực của những cạnh đồng quy bên trên một điểm và điểm đồng quy tê liệt đó là tâm của đàng tròn xoe nước ngoài tiếp nhiều giác.
Các em học viên hoàn toàn có thể xem thêm thêm thắt bài xích viết:
Cách xác lập tâm đàng tròn xoe nước ngoài tiếp
Chứng minh tứ giác nội tiếp
2. Đường tròn xoe nội tiếp
a) Định nghĩa
Đường tròn xoe xúc tiếp với toàn bộ những cạnh của một nhiều giác được gọi là đàng tròn xoe nội tiếp
tam giác và nhiều giác được gọi là nhiều giác nước ngoài tiếp đàng tròn xoe.
Ví dụ: Đường tròn xoe tâm O nhập hình bên dưới là đàng tròn xoe nội tiếp vì thế nó xúc tiếp với toàn bộ cạnh của nhiều giác.
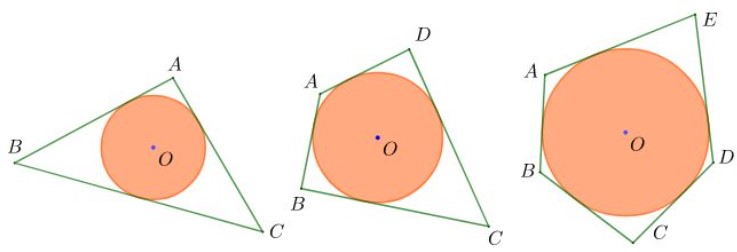
Khi tê liệt, Khi tê liệt, ΔABC, tứ giác CBAD và ngũ giác ABCDE được gọi theo thứ tự là tam giác nước ngoài tiếp, tứ giác nước ngoài tiếp và ngũ giác nước ngoài tiếp đàng tròn xoe tâm O (đa giác ở bên phía ngoài đàng tròn xoe tâm O).
b) Cách xác lập tâm đàng tròn xoe nội tiếp tam giác
Tâm đàng tròn xoe nội tiếp nhiều giác là phú (∩) của những đàng phân giác của toàn bộ những góc nhập một nhiều giác.
Để hoàn toàn có thể xác lập tâm đàng tròn xoe nội tiếp một nhiều giác, tớ cần thiết thực hiện như sau:
- Kẻ những đàng phân giác của những góc tiếp sau đó xác lập phú điểm.
- Kẻ đường thẳng liền mạch trải qua phú điểm và vuông góc với cùng 1 cạnh ngẫu nhiên nhằm mục tiêu xác lập nửa đường kính.
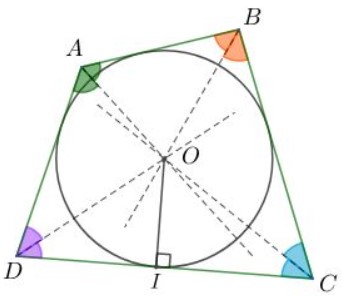
Vậy nên, một nhiều giác sở hữu đàng tròn xoe nội tiếp khi đàng phân giác của những góc nhập đồng quy và điểm đồng quy đó là tâm của đàng tròn xoe nội tiếp nhiều giác tê liệt.
3. Định lý
Bất kỳ nhiều giác nào thì cũng đều phải sở hữu một và duy nhất đàng tròn xoe nước ngoài tiếp, sở hữu một và chỉ một
đường tròn xoe nội tiếp.
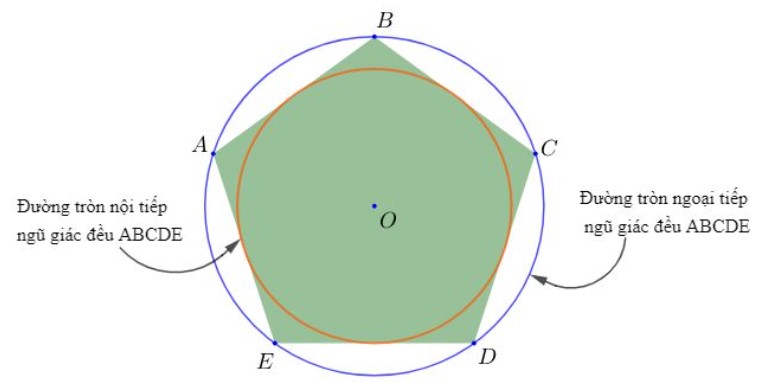
Ngũ giác đều ABCDE sở hữu một đàng tròn xoe nội tiếp và một đàng tròn xoe nước ngoài tiếp. điều đặc biệt, tâm đàng tròn xoe nước ngoài tiếp và tâm đàng tròn xoe nội tiếp ngũ giác đều ABCDE trùng nhau, đều là tâm o.
Chú ý: Tâm của một đàng tròn xoe nước ngoài tiếp trùng với tâm đàng tròn xoe nội tiếp và được gọi là tâm của nhiều giác đều.
Bài tập dượt tự động luận
Bài 1: (61/91/SGK TOÁN 9T2)
a) Vẽ một đàng tròn xoe tâm O với nửa đường kính 2cm.
b) Vẽ một hình vuông vắn nội tiếp đàng tròn xoe (O) bám theo câu a.
c) Tính chừng nhiều năm nửa đường kính r của đàng tròn xoe nội tiếp hình vuông vắn tìm kiếm ra ở câu b rồi vẽ đàng tròn xoe tâm O sở hữu nửa đường kính r
Lời giải:
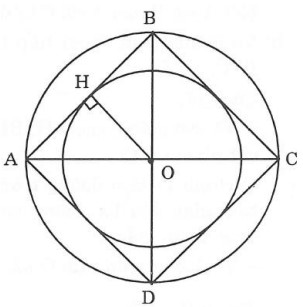
a) Vẽ đàng tròn xoe tâm O với nửa đường kính vì chưng 2cm.
b) Vẽ nhị 2 lần bán kính AC và BD vuông góc cùng nhau bên trên tâm O. Nối 4 điểm A, B, C và D lại cùng nhau tớ đã có được hình vuông vắn ABCD nội tiếp đàng tròn xoe tâm O sở hữu nửa đường kính nhiều năm 2cm.
c) Kẻ đàng cao OH ứng với cạnh AB (H ∈ AB) .
ΔAOB sở hữu OA = OB (=R) => ΔAOB cân nặng bên trên O.
Lại có: Góc AOB = 90° (vì AC ⊥ BD bám theo đặc thù đàng chéo cánh của hình vuông vắn, nên ΔAOB vuông cân nặng bên trên O).
=> R = OH = (OB√2)/2 = √2 (cm)
Bài 2: (62/91/SGK TOÁN 9 T2)
a) Vẽ tam giác đều ABC sở hữu cạnh a = 3 centimet.
b) Vẽ tiếp tuyến phố tròn xoe (O ; R) nước ngoài tiếp tam giác đều ABC, tính R.
c) Vẽ đàng tròn xoe tâm O, phân phối kinh r nội tiếp tam giác đều ABC, thám thính r.
d) Vẽ tam giác IJK đều nước ngoài tiếp đàng tròn xoe (O ; R).
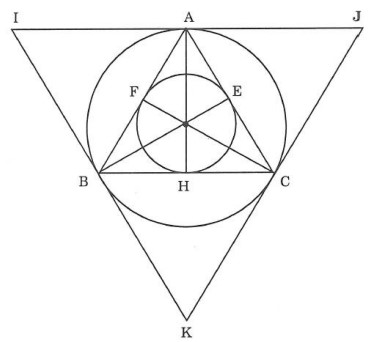
a) Cách vẽ: Muốn vẽ một tam giác đều ABC sở hữu cạnh nhiều năm 3cm tớ vẽ:
– Vẽ đoạn trực tiếp BC nhiều năm 3cm.
– Lấy B thực hiện tâm vẽ cung tròn xoe nửa đường kính 3cm.
– Lấy C thực hiện tâm vẽ cung tròn xoe phân phối 3cm.
– Cũng bên trên tâm B và cũng bên trên tâm C hạn chế nhau bên trên A.
Nối A với B, nối A với C tớ được tam giác đều ABC cạnh có tính nhiều năm 3cm.
Xem thêm: Ca-ta (Qatar) | Hồ sơ - Sự kiện - Nhân chứng
b) Cách vẽ:
– Vẽ những đàng cao AH, BE ứng với cạnh BC và cạnh AC. AH và BE hạn chế nhau bên trên O.
O đó là tâm đàng tròn xoe nước ngoài tiếp ΔABC vì thế O cơ hội đều A, B, C (Tam giác đều ba
đường cao mặt khác phụ vương đàng trung tuyến, trung trực, phân giác).
– Vẽ tiếp đàng tròn xoe tâm O sở hữu nửa đường kính OA = R.
Ta có: R = OA = 2/3 AH = 2/3. (AB√3)/3 = √3 (cm)
c) Đường tròn xoe nội tiếp một tam giác sở hữu tâm là phú điểm của phụ vương đàng phân giác nhập của
tam giác tê liệt.
Vì ABC là tam giác nên O là phú điểm của phụ vương đàng cao AH, BE, CF mặt khác O cũng
là tâm của đàng tròn xoe nội tiếp tam giác này.
Vẽ đàng tròn xoe tâm O nửa đường kính OH = r là đàng tròn xoe nội tiếp ΔABC.
Theo đặc thù phụ vương đàng trung tuyến của tam giác thì OA = 1/3AH.
ΔAHB vuông bên trên H (tam giác đều đàng phân giác cũng chính là đàng cao) nên:
AB² = AH² + HB² (Định lí Pi-ta-go).
=> AH² = AB² – HB² = a² – (a/2)² = a² – a²/4 = 3a²/4
=> AH = (a√3)/2
Mà OH = 1/3 AH => OH = r = 1/3.(a√3)/2 = √3/2 (a = 3 cm)
d) thạo rằng tam giác nước ngoài tiếp đàng tròn xoe, thì đàng tròn xoe nội tiếp tam giác tê liệt.
Do tê liệt tam giác đều IJK nước ngoài tiếp đàng tròn xoe (O ; R) thì đàng tròn xoe (O ; R) nội tiếp tam giác này => Tâm O của (O ; R) đó là phú điểm của phụ vương đàng trung trực, phân giác, đàng cao của tam giác đều IJK. Từ tê liệt tớ sở hữu phương pháp vẽ.
Vẽ phụ vương đường thẳng liền mạch ứng với OA, OB, OC bên trên A, B, C phụ vương đường thẳng liền mạch này hạn chế nhau bên trên I, J, K.
IJK đó là tam giác đều nên vẽ.
Bài tập dượt trắc nghiệm
Câu 1: Tính chừng nhiều năm cạnh của tam giác đều nội tiếp (O; R) bám theo R
A. R/√3
B. √3R
C. R√6
D. 3R
Lời giải:
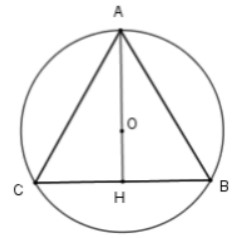
Gọi tam giác nội tiếp đàng tròn xoe (O; R) là ΔABC đều cạnh a. Khi tê liệt tớ sở hữu O là trọng tâm của tam giác ABC. Gọi đàng trung tuyến là AH.
=> R = AO = 2/3 AH => AH = 3R/2
Theo quyết định lý Pytago tớ có:
AH² = AB² – BH² = 3a²/4 => AH = (a√3)/2
Từ đó: 3R/2 = (a√3)/2 => a = √3R
Vậy B là đáp án cần thiết tìm
Câu 2: Tính diện tích S của một tam giác đều nội tiếp đàng tròn xoe tâm O, nửa đường kính 2cm.
A. 6 cm².
B. 6√3 cm².
C. 3 cm².
D. 3√3 cm².
Lời giải:
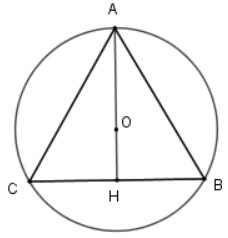
Gọi tam giác nội tiếp đàng tròn xoe (O; 2cm) là ΔABC đều cạnh a. Khi tê liệt tớ sở hữu điểm O là trọng tâm tam giác ABC và cũng chính là của tâm đàng tròn xoe nước ngoài tiếp tam giác ABC => AO = 2cm.
Gọi đàng trung tuyến là AH => 2/3AH = AO = 2cm => AH = 3cm
Theo quyết định lý Pytago tớ có:
AH² = AB² – BH² = 3a²/4 => AH = (a√3)/2
Mà AH = 3cm => 3 = (a√3)/2 => a = 2√3 cm
Diện tích tam giác ABC là: S ΔABC = một nửa.AH.BC = một nửa x 3 x 2√3 = 3√3 cm²
Vậy D là đáp án cần thiết tìm
Câu 3: Cho đàng tròn xoe tâm O sở hữu nửa đường kính = 4. Dây AC có tính nhiều năm vì chưng cạnh hình vuông vắn nội tiếp và chão BC có tính nhiều năm vì chưng cạnh tam giác đều nội tiếp đàng tròn xoe tê liệt (Hai điểm A và C ở nằm trong phía với BO). Tìm số đo góc ACB?
A. 30°
B. 45°
C. 60°
D. 15°
Lời giải:
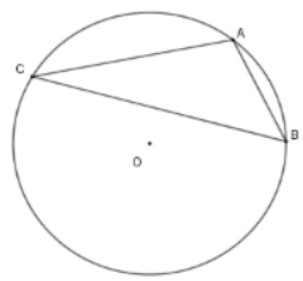
- Vì AC vì chưng cạnh của hình vuông vắn nội tiếp (O) => số đo cung AC = 90°.
- Vì BC vì chưng cạnh của tam giác đều nội tiếp (O) => số đo cung BC = 120°.
=> Số đo cung AB = 120° – 90° = 30°
Vì góc Ngân Hàng Á Châu ACB là góc nội tiếp chắn cung AB => góc Ngân Hàng Á Châu ACB = 30°/2 = 15°.
Vậy D là đáp án cần thiết tìm
Xem thêm: Tổng quan về ảnh hình trắng
Xem full 30 câu trắc nghiệm về Đường tròn xoe nước ngoài tiếp – Đường tròn xoe nội tiếp:
Mong rằng qua chuyện nội dung bài viết này những em học viên tiếp tục tóm có thể được kiến thức và kỹ năng về Đường tròn xoe nước ngoài tiếp. Đường tròn xoe nội tiếp và áp dụng được nhập bài xích tập dượt của tớ. Thường xuyên truy vấn nhập beyeu.edu.vn nhằm update những nội dung bài viết mới nhất và xem thêm nhiều tư liệu hữu dụng của không ít cỗ môn nhé!
