Cách tính thể tính hình hộp chữ nhật chính xác và dễ nhớ

Hình vỏ hộp chữ nhật là gì?

Hình vỏ hộp chữ nhật là một trong hình dạng học tập không khí với 6 mặt mày đều là hình chữ nhật. Trong số đó, với 2 mặt mày không tồn tại cạnh công cộng gọi là 2 mặt mày đối lập hay những mặt mày lòng, còn những mặt mày sót lại gọi là mặt mày mặt mày. 

Bạn đang xem: Cách tính thể tính hình hộp chữ nhật chính xác và dễ nhớ

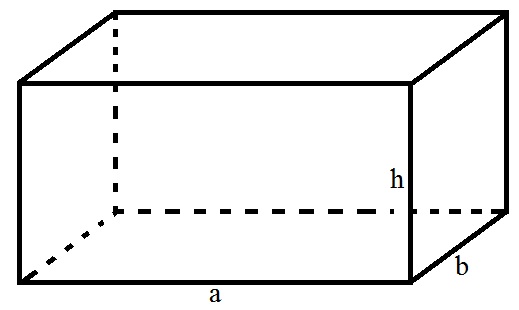
Một số đặc điểm của hình vỏ hộp chữ nhật:

• Hình chữ nhật với 12 cạnh, 8 đỉnh và 6 mặt mày.

• Các lối chéo cánh với 2 đầu mút là 2 đỉnh đối nhau của hình vỏ hộp chữ nhật đồng quy bên trên 1 điểm

• Diện tích của 2 mặt mày đối lập nhập hình vỏ hộp chữ nhật bởi vì nhau

• Chu vi của 2 mặt mày đối lập nhập hình vỏ hộp chữ nhật bởi vì nhau

Công thức tính thể tích hình vỏ hộp chữ nhật

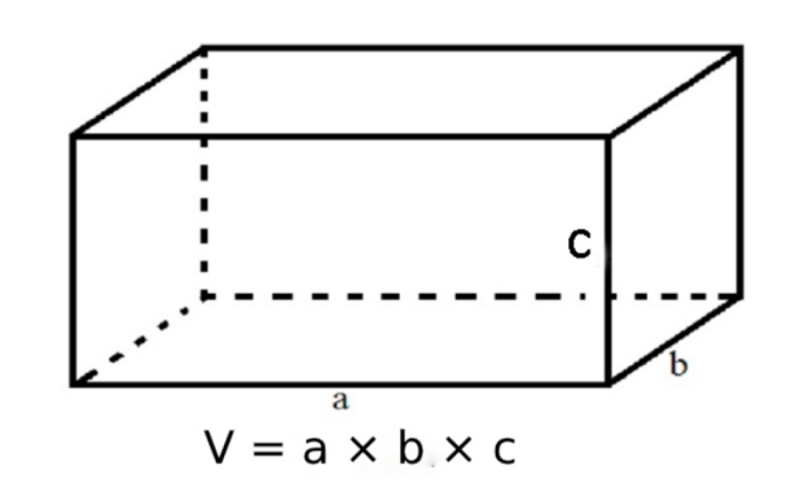
Công thức tính thể tích hình vỏ hộp chữ nhật là nhân chiều lâu năm của mặt mày lòng (dài) với chiều rộng lớn của mặt mày lòng (rộng), tiếp sau đó nhân với độ cao của khối vỏ hộp. 

Công thức tổng quát lác là: Thể tích (V) = Chiều lâu năm (dài) * chiều rộng lớn (rộng) * độ cao (cao), hoặc V = drc = a*b*c. Trong đó:

• V: thể tích hình vỏ hộp chữ nhật.

• a: chiều lâu năm hình vỏ hộp chữ nhật.

• b: chiều rộng lớn hình vỏ hộp chữ nhật.

• h: chiều cao hình vỏ hộp chữ nhật.

Một số phương pháp tính thể tích hình vỏ hộp chữ nhật khác

Ngoài phương pháp tính theo gót công thức tổng quát lác, chúng ta có thể tính thể tích hình vỏ hộp chữ nhật bởi vì những cơ hội sau:

Cách 1: Cách tính tổng diện tích S của thân phụ mặt mày mặt và cạnh bởi vì nhau

Công thức này là: V = 2(ab + ac + bc), nhập bại a và b theo thứ tự là chiều lâu năm và chiều rộng lớn, c là độ cao.

Ví dụ:

Cho một vỏ hộp chữ nhật với chiều lâu năm a = 5 centimet, chiều rộng lớn b = 3 centimet và độ cao c = 4 centimet.

Ta rất có thể tính thể tích bằng phương pháp tính tổng diện tích S những mặt mày mặt và cạnh đều bằng nhau.

S = 2(a*b + a*4 + b*c) = 2(5*3 + 5*4 + 3*4) = 94 cm^3

Cách 2: Cách tính thể tích lúc biết diện tích S mặt mày lòng của hình vỏ hộp chữ nhật

Nếu diện tích S mặt mày lòng (Sd) của hình vỏ hộp chữ nhật đang được biết, chúng ta có thể tính được 1 trong các nhị thông số kỹ thuật sót lại như a hoặc b (chiều lâu năm hoặc chiều rộng). Với chiều lâu năm và chiều rộng lớn là nhị độ cao thấp của mặt mày lòng, tớ với công thức Sd = a*b. Dựa bên trên công thức này, tớ rất có thể đo lường và dò thám đi ra thông số kỹ thuật bị thiếu hụt.

Sau khi chúng ta đang được xác lập được toàn bộ những thông số kỹ thuật quan trọng, hãy dùng công thức V = a*b*c (nếu chúng ta đang được biết a, b và c) nhằm đo lường thể tích của khối vỏ hộp chữ nhật.

Cách 3: Công thức tính thể tích lúc biết chu vi khối chữ nhật

Nếu chu vi (C) của hình vỏ hộp chữ nhật đang được biết, chúng ta nên biết tối thiểu nhị nhập thân phụ thông số kỹ thuật sót lại (a, b và c). Chu vi C được xem bởi vì công thức: C = 4a + 4b + 4c. 

Sau khi chúng ta đang được xác lập được toàn bộ những thông số kỹ thuật quan trọng, hãy dùng công thức V = a*b*c (nếu chúng ta đang được biết a, b và c) nhằm đo lường thể tích của khối vỏ hộp chữ nhật.

Các dạng bài bác luyện về kiểu cách tính thể tích hình vỏ hộp chữ nhật và cách thức giải

Đối với đề chính tính thể tích của khối vỏ hộp chữ nhật, những em sẽ tiến hành thích nghi với một số trong những dạng bài bác luyện cơ bạn dạng sau đây:

Dạng 1: Cách tính thể tích của một vỏ hộp chữ nhật lúc biết chiều lâu năm, chiều rộng lớn và độ cao.

Ví dụ: Cho hình vỏ hộp chữ nhật biết chiều lâu năm 6cm, chiều rộng lớn 3cm và độ cao 2cm. Tính thể tích hình bại.

Hướng dẫn giải:

Thể tích hình vỏ hộp chữ nhật là:

V = l x w x h

V = 6cm x 3cm x 2cm

V = 36cm^3

Dạng 2: Cho hình vỏ hộp chữ nhật biết thể tích, nhị độ cao thấp ứng và đòi hỏi tính độ cao thấp cạnh sót lại.

Ví dụ: Tính chiều rộng lớn của một vỏ hộp chữ nhật rất có thể tích 240cm^3, chiều lâu năm 8cm và độ cao 5cm.

V = l x w x h240cm^3 = 8cm x w x 5cmw = 6cm

Dạng 3: Tính độ cao hình vỏ hộp chữ nhật lúc biết 2 độ cao thấp cạnh và thể tích tương ứng

Ví dụ: Cho hình vỏ hộp chữ nhật, biết thể tích 420cm^3, chiều lâu năm 14cm và chiều rộng lớn 3cm. Tính độ cao của hình?

V = l x w x h420cm^3 = 14cm x 3cm x hh = 10cm

Dạng 4: Cách tính thể tích của một số trong những vỏ hộp chữ nhật được hạn chế quăng quật một trong những phần.

Ví dụ: Cho hình vỏ hộp chữ nhật biết chiều lâu năm 12cm, chiều rộng lớn 6cm và độ cao 3cm nếu như một trong những phần của vỏ hộp bị hạn chế quăng quật. Thể tích hình là bao nhiêu?

V = l x w x hV = (12cm x 6cm x 3cm) - (4cm x 3cm x 3cm)V = 648cm^3 - 36cm^3V = 612cm^3

Dạng 5: Tính thể tích của một vỏ hộp chữ nhật Khi với 1 lỗ hình tròn trụ được đục thoát khỏi một phía phẳng lặng của chính nó.

Ví dụ: Cho hình vỏ hộp chữ nhật với chiều lâu năm 10cm, chiều rộng lớn 8cm và độ cao 6cm nếu như một lỗ hình tròn trụ nửa đường kính 2cm được đục thoát khỏi một phía phẳng lặng của chính nó. Thể tích hình là bao nhiêu?

V = l x w x hV = (10cm x 8cm x 6cm) - (pi x 2cm^2 x 6cm)V = 480cm^3 - 75.4cm^3V = 404.6cm^3

Dạng 6:. Cách tính thể tích của một vỏ hộp chữ nhật Khi một góc của chính nó bị hạn chế quăng quật.

Ví dụ: Cho hình vỏ hộp chữ nhật với chiều lâu năm 8cm, chiều rộng lớn 6cm và độ cao 4cm nếu như một góc của chính nó bị hạn chế quăng quật. Thể tích hình là bao nhiêu?

V = l x w x hV = (8cm x 6cm x 4cm) - (2cm x 2cm x 4cm)V = 192cm^3 - 16cm^3V = 176cm^3

Dạng 7: Tính thể tích của một số trong những vỏ hộp chữ nhật không đồng đều, với những mặt mày phẳng lặng chéo nhau.

Ví dụ: Cho hình vỏ hộp chữ nhật không đồng đều, với chiều lâu năm 10cm, chiều rộng lớn 5cm và độ cao 4cm. Mặt phẳng lặng bên dưới nằm trong của vỏ hộp là một trong hình tam giác đều với cạnh 6cm. Tính thể tích của hình.

V = l x w x hV = (10cm x 5cm x 4cm) + (1/2 x 6cm x 4cm)V = 200cm^3 + 12cm^3V = 212cm^3

Xem thêm: Công thức tính thể tích hình lập phương & chỉ dẫn giải chi tiết

Xem thêm: Ca-ta (Qatar) | Hồ sơ - Sự kiện - Nhân chứng

Bài thói quen thể tích hình vỏ hộp chữ nhật cơ bạn dạng cho tới nâng cao

Dựa nhập những kỹ năng và kiến thức bên trên, sau đây Monkey tiếp tục tổ hợp một số trong những bài bác luyện tương quan kể từ cơ bạn dạng cho tới nâng lên nhằm những em rất có thể áp dụng và giải bài bác luyện nhé!

Các bài bác luyện về kiểu cách tính thể tích hình vỏ hộp chữ nhật cơ bản

Bài 1: Hình vỏ hộp chữ nhật với chiều lâu năm 8 m, chiều rộng lớn 5 m và độ cao 6 m. Tính lối chéo cánh của hình vỏ hộp chữ nhật.

Bài 2: Một hồ nước chứa chấp nước với hình dạng vỏ hộp chữ nhật rất có thể tích là 3000 m3, chiều rộng lớn là 10 m và độ cao của hồ nước là 12 m. Tính chiều lâu năm của hồ nước.

Bài 3:  Cho hình vỏ hộp chữ nhật với chiều lâu năm là 2,5cm, chiều rộng lớn là một,8 centimet và độ cao là 2cm. Hãy tính thể tích, diện tích S xung xung quanh, diện tích S toàn phần của hình vỏ hộp chữ nhật bại bại.

Bài 4: Cho hình vỏ hộp chữ nhật ABCD.A'B'C'D' với diện tích S lòng SABCD = 24cm2 và rất có thể tích V = 84 cm3. Chiều cao của hình vỏ hộp chữ nhật có tính lâu năm là?

Bài 5: Tính thể tích của khối vỏ hộp ABCD.A'B'C'D', hiểu được AA'B'D' là khối tứ diện đều cạnh a.

Bài 6: Một bể nước hình vỏ hộp chữ nhật với chiều lâu năm 2m. Lúc đầu bể không tồn tại nước. Sau Khi sụp đổ nhập bể 120 thùng nước, từng thùng chứa chấp trăng tròn lít thì mực nước của bể là 0,8m.

a) Tính chiều rộng lớn của bể nước.

b) Người tớ sụp đổ thêm nữa bể 60 thùng nước nữa thì lênh láng bể. Hỏi bể cao từng nào mét?

Các bài bác luyện vận dụng công thức tính thể tích hình vỏ hộp chữ nhật nâng cao 

Trong lịch trình lớp 8 và lớp 12, những em sẽ tiến hành không ngừng mở rộng kỹ năng và kiến thức về mặt mày phẳng lặng. Vì vậy, ngoài dạng bài bác tính thể tích hình vỏ hộp chữ nhật, những em sẽ tiến hành thích nghi với những dạng toán xác lập thể tích tối đa/ ít nhất, đối chiếu thể tích 2 khối vỏ hộp & những Việc phần mềm thực tiễn. 

Bài 1:  Cho một hình vỏ hộp chữ nhật với những độ cao thấp tỉ trọng với 3; 4; 5 và thể tích của hình vỏ hộp là 60cm3. Tính thể tích lớn số 1 của khối vỏ hộp bại.

Bài 2: Hình lập phương A với cạnh bằng 

$\frac{1}{2}$ cạnh hình lập phương B. Hỏi thể tích hình lập phương A bởi vì từng nào phần thể tích hình lập phương B

Bài 3: Một bể cá hình dạng vỏ hộp chữ nhật bởi vì kính (không nắp) với chiều lâu năm 1 m, chiều rộng lớn 70 centimet, độ cao 60 centimet. Mực nước nhập bể cao 30 centimet. Người đi ra mang đến nhập bể một hòn đá thì thể tích tăng 14000 cm3. Hỏi mực nước nhập bể thời điểm hiện nay cao từng nào. 

Đáp án bài bác thói quen thể tích hình vỏ hộp chữ nhật nâng cao

Bài 1: 

Gọi độ cao thấp của hình vỏ hộp chữ nhật đang được mang đến là  a, b, c

Vì những độ cao thấp tỉ trọng với 3; 4; 5 nên:

$\frac{\mathrm{a}}{3}=\frac{\mathrm{b}}{4}=\frac{\mathrm{c}}{5}=\mathrm{t}$

Thể tích của hình vỏ hộp là:

 V = abc nên: 3t. 4t. 5t= 480

Suy ra:  60t3 = 60 nên t = 1

Do bại, a = 3cm; b = 4cm; c = 5cm

Vậy cạnh lớn số 1 của hình vỏ hộp là 5cm

Bài 2:

Gọi chiều lâu năm một cạnh của hình lập phương A là a.

Vì hình lập phương A với cạnh bằng $\frac{1}{2}$cạnh của hình lập phương B nên chiều lâu năm 1 cạnh của hình lập phương B là 2a

Thể tích hình lập phương A là:

VA = a3.

Thể tích hình lập phương B là:

VB = (2a)3 = 8a3

=> VB = 8VA

=> VA = $\frac{1}{8}$VB

Vậy thể tích hình lập phương A bằng $\frac{1}{8}$ thể tích hình lập phương B

Bài 3:

Đổi 1m = 100 cm

Thể tích phần bể chứa chấp nước thuở đầu là:

 V = 100.70.30 = 210000 cm3

Sau Khi mang đến vào một trong những hòn đá thể tích tăng 14000 cm3. Vậy thể tích phần bể chứa chấp nước khi sau là:

V1 = V + 14000

= 210000 + 14000 = 224000 cm3

Vì chiều lâu năm và chiều rộng lớn bể nước không bao giờ thay đổi nên sự thay cho thay đổi là vì độ cao mực nước thay cho thay đổi. Gọi độ cao mực nước khi sau là h centimet. Ta có:

V = 100.70.h = 224000

=> h =  = 32 cm

Bí quyết nắm rõ phương pháp tính thể tích V hình vỏ hộp chữ nhật

Để canh ty những em học tập kỹ năng và kiến thức này dễ dàng nắm bắt, dễ dàng vận dụng rộng lớn Khi giải toán hoặc phần mềm nhập thực tiễn đưa thì bên dưới đấy là một số trong những kinh nghiệm tay nghề nhằm quý khách tham lam khảo:

Nắm chắc hẳn kỹ năng và kiến thức cơ bạn dạng về hình vỏ hộp chữ nhật

Để giải được bài bác luyện về tính chất thể tích hình vỏ hộp chữ nhật, yên cầu những em nên tóm chắc hẳn được những kỹ năng và kiến thức tương quan cho tới hình học tập này, kể từ định nghĩa, đặc điểm, Đặc điểm, công thức tính và cơ hội giải những dạng bài bác luyện tương ứng….Ba u nên dành riêng thời hạn nhằm chỉ dẫn nhỏ bé học tập và soát lại bài bác cũ của con cái, nhằm hiểu rằng nhỏ bé đang được bắt gặp trở ngại ở trong phần nào là, nhằm kể từ bại củng cổ, phân tích và lý giải nhằm rời hiện tượng con cái “học trước quên sau”.

Luyện luyện thực hành thực tế thông thường xuyên

Học song song với hành là nguyên tố nên nếu như muốn làm rõ được kỹ năng và kiến thức tôi đã học tập. Vậy nên, thân phụ u nên khuyến khích, đòi hỏi nhỏ bé nên thực hành thực tế, thực hiện bài bác luyện về tính chất thể tích khối hình vỏ hộp chữ nhật, hoặc ngẫu nhiên bài bác luyện nào là thông thường xuyên rộng lớn. Bên cạnh đó, rất có thể mang đến con cái nhập cuộc những cuộc ganh đua, tổ chức triển khai trò đùa, nhập cuộc những hoạt động và sinh hoạt về toán học… Qua bại canh ty kích ứng kĩ năng suy nghĩ và năng lượng toán học tập của nhỏ bé đảm bảo chất lượng rộng lớn.

Tạo sự hào hứng khi tham gia học toán hình nằm trong Monkey Math

Monkey Math được nghe biết là ứng dụng dạy dỗ học tập toán online giành cho trẻ em thiếu nhi và tè học tập, với nội dung được thiết kế bám sát lịch trình GDPT tiên tiến nhất của Sở thể hiện. Như vậy góp thêm phần canh ty nhỏ bé một vừa hai phải cải cách và phát triển năng lượng học tập toán, một vừa hai phải tương hỗ việc học tập bên trên ngôi trường lớp đạt thành phẩm đảm bảo chất lượng rộng lớn.

Điểm đặc trưng của Monkey Math đó là không dạy dỗ học tập theo gót cách thức truyền thụ kỹ năng và kiến thức thường thì, thay cho nhập này sẽ vận dụng những phương pháp dạy dỗ học tập tích cực kỳ như trải qua trò đùa, những hoạt động và sinh hoạt tương tác, thách thức mừng, sách bài bác luyện trượt trợ… Qua bại canh ty nhỏ bé dễ dàng và đơn giản với sự hào hứng và niềm yêu thương mến khi tham gia học toán rộng lớn.

Xem thêm: Tất cả công thức lý 11 học kì 1 : Những kiến thức cơ bản mà bạn cần nắm vững

Đồng thời, nội dung bài học kinh nghiệm bên trên phần mềm tổ hợp đa dạng đề chính kể từ đại số cho tới hình học, bao hàm cả chủ thể về hình vỏ hộp chữ nhật. Tất cả được phân tạo thành nhiều Lever kể từ dễ dàng cho tới khó, cá thể hoá mang đến từng đối tượng người sử dụng nhằm cha mẹ dễ dàng và đơn giản lựa lựa chọn Lever thích hợp nhất với nhỏ bé.

Đảm bảo từng giờ học tập toán nằm trong Monkey Math với nhỏ bé là từng nụ cười, na ná kích ứng kĩ năng suy nghĩ và năng lượng toán học tập của trẻ em cải cách và phát triển rộng lớn thường ngày. Để làm rõ rộng lớn về phần mềm, thân phụ u rất có thể xem thêm Clip sau, hoặc ĐK sẽ được tư vấn không lấy phí nhé.

Trên đấy là những vấn đề canh ty quý khách làm rõ rộng lớn về kiểu cách tính thể tích hình vỏ hộp chữ nhật.  Đây là kỹ năng và kiến thức không những vận dụng nhập toán học tập nhưng mà nhập thực tiễn đưa phần mềm thật nhiều, nên thân phụ u hãy xem thêm để sở hữu tăng vấn đề chỉ dẫn nhỏ bé học tập đảm bảo chất lượng rộng lớn. Đồng thời, nếu như không tồn tại nhiều thời hạn và kinh nghiệm tay nghề trong các việc dạy dỗ nhỏ bé học tập toán thì rất có thể xem thêm phần mềm Monkey Math nhé.