Công thức tính bán kính hình tròn theo 4 cách đơn giản có ví dụ cụ thể - Thegioididong.com

Hình tròn trĩnh là 1 trong trong mỗi hình thường trông thấy vô thực tiễn (ví dụ: bánh xe pháo, đồng hồ thời trang, ngược bóng,…). Vậy nửa đường kính hình tròn trụ là gì? Công thức tính bán kính của hình tròn trụ nếu như biết những thông số kỹ thuật như 2 lần bán kính, chu vi, diện tích S như vậy nào?

Xem thêm: Đối Tượng AutoCAD Bị Mờ: Nguyên Nhân Và Cách Xử Lý

Xem thêm: #1 Lệnh UCS vô Cad – Cách dùng Autocad cụ thể 2021

Bạn đang xem: Công thức tính bán kính hình tròn theo 4 cách đơn giản có ví dụ cụ thể - Thegioididong.com

1. Bán kính hình tròn trụ là gì?

Khái niệm

Bán kính của một đàng tròn trĩnh là khoảng cách từ là một điểm ngẫu nhiên bên trên đàng tròn trĩnh cho tới tâm của đàng tròn trĩnh cơ. Độ lâu năm của nửa đường kính đàng tròn trĩnh vì thế 1/2 2 lần bán kính của đàng tròn trĩnh cơ.

Ký hiệu

Bán kính thông thường được ký hiệu bằng văn bản r.

– Được sử dụng vô đa số những công thức tương quan cho tới đo lường hình tròn trụ như:

+ Chu vi hình tròn trụ.

+ Diện tích hình tròn trụ.

+ Phương trình đàng tròn trĩnh.

2. Tính nửa đường kính đàng tròn trĩnh lúc biết đàng kính

Bán kính của hình tròn trụ luôn luôn trực tiếp vì thế 1/2 chừng lâu năm của 2 lần bán kính.

Công thức

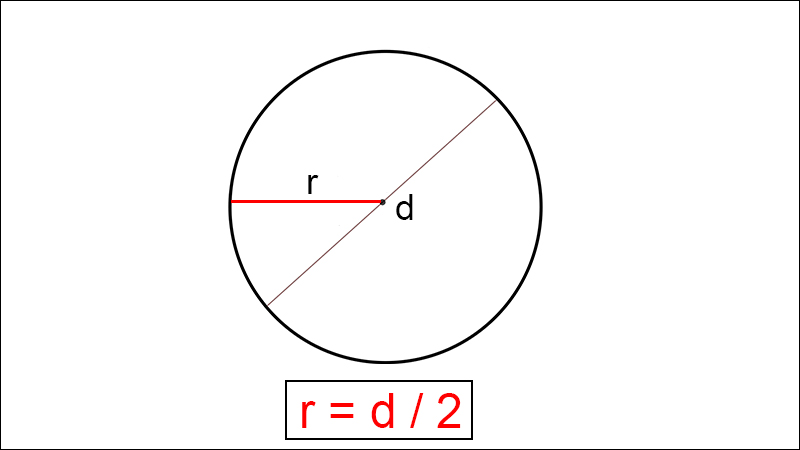
Công thức tính bán kính đàng tròn trĩnh lúc biết đàng kính

Trong đó:

+ r : Bán kính đàng tròn trĩnh.

+ d : Đường kính đàng tròn trĩnh.

Ví dụ: Tính nửa đường kính đàng tròn trĩnh biết 2 lần bán kính hình tròn trụ là 10 centimet.

​

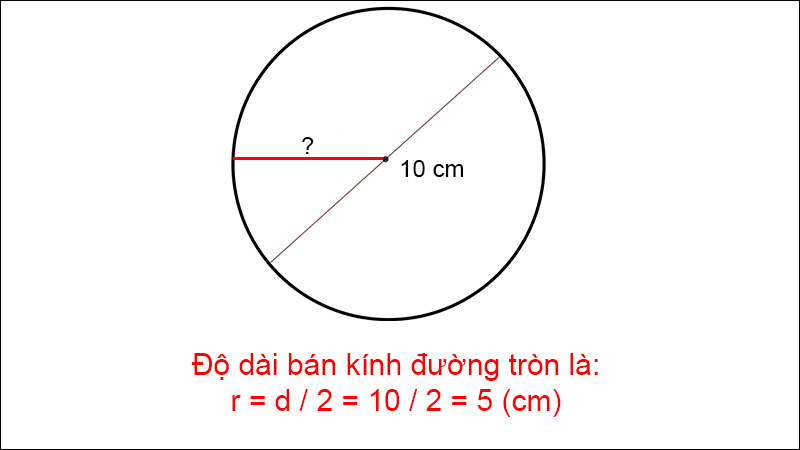
Ví dụ tính bán kính đàng tròn trĩnh lúc biết đàng kính

3. Tính nửa đường kính đàng tròn trĩnh lúc biết chu vi

Công thức

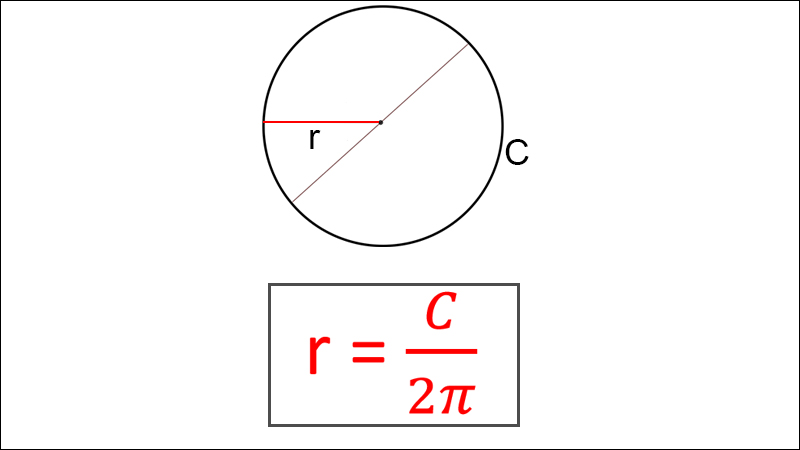
Công thức tính bán kính đàng tròn trĩnh lúc biết chu vi

Trong đó:

+ r : Bán kính đàng tròn trĩnh.

+ C : Chu vi hình tròn trụ.

+ π : Số pi, có mức giá trị xấp xỉ 3,14.

Bạn rất có thể người sử dụng độ quý hiếm xấp xỉ 3.14 vô phép tắc tính hoặc người sử dụng ký hiệu π bên trên PC di động.

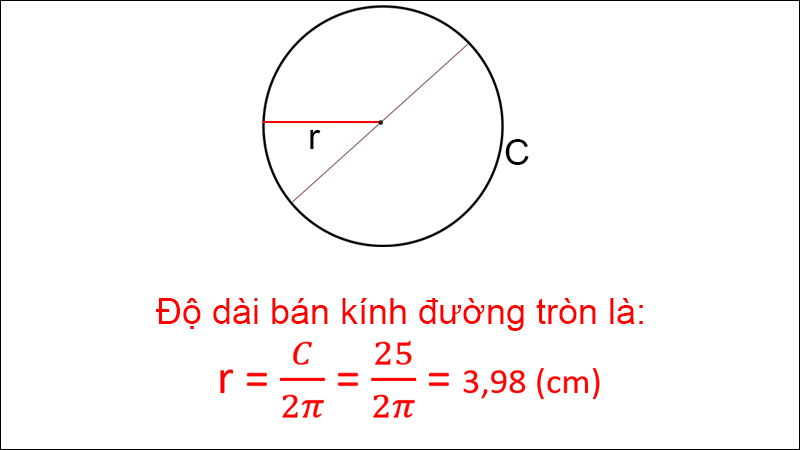
Ví dụ: Tính nửa đường kính đàng tròn trĩnh biết chu vi hình tròn trụ là 25 centimet.

Xem thêm: Bộ sưu tập hình ảnh Phật Tổ Như Lai đẹp nhất, đầy đủ chất lượng Full HD

Ví dụ tính bán kính đàng tròn trĩnh lúc biết chu vi

4. Tính nửa đường kính đàng tròn trĩnh lúc biết diện tích

Công thức

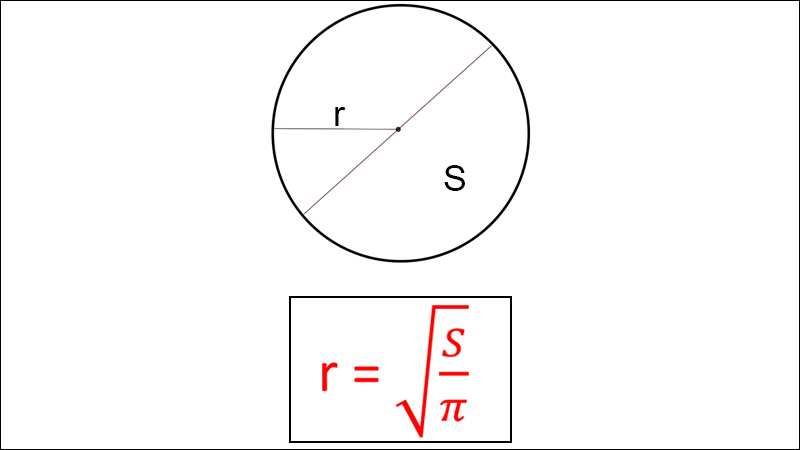
Công thức tính bán kính đàng tròn trĩnh lúc biết diện tích

Trong đó:

+ r : Bán kính đàng tròn trĩnh.

+ S : Diện tích hình tròn trụ.

+ π : Số pi, có mức giá trị xấp xỉ 3,14.

Ví dụ: Tính nửa đường kính đàng tròn trĩnh biết diện tích S hình tròn trụ là 80 cm2.

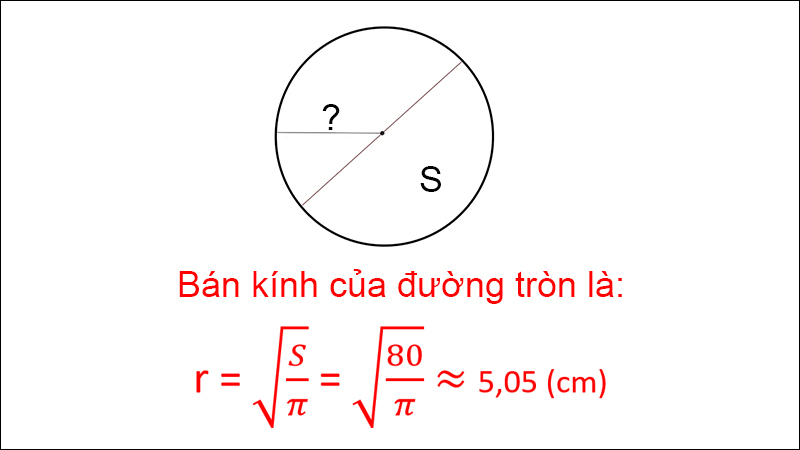
Ví dụ tính bán kính đàng tròn trĩnh lúc biết diện tích

5. Tính nửa đường kính đàng tròn trĩnh lúc biết diện tích S và góc ở tâm của hình quạt

Công thức

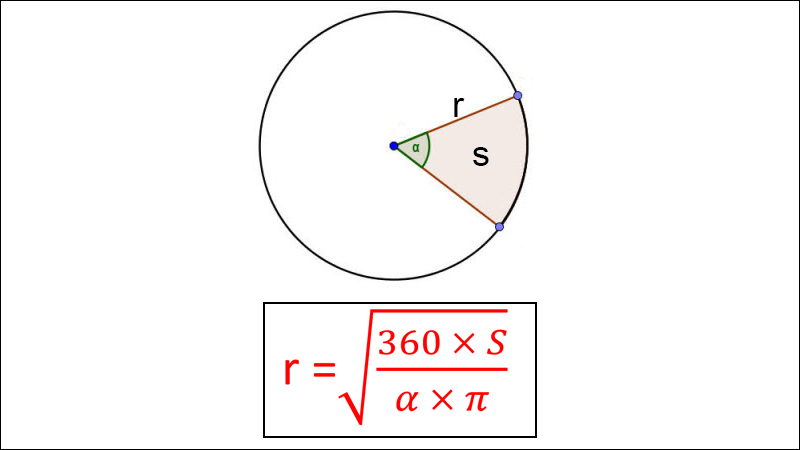
Công thức tính bán kính đàng tròn trĩnh lúc biết diện tích S và góc ở tâm của hình quạt

Trong đó:

+ r : Bán kính đàng tròn trĩnh.

+ S : Diện tích hình tròn trụ.

+ α : Góc ở tâm của hình quạt tính vì thế chừng.

+ π : Số pi, có mức giá trị xấp xỉ 3,14

Ví dụ: Tính nửa đường kính đàng tròn trĩnh biết diện tích S hình quạt là 25,7 cm2 và góc ở tâm của hình quạt là 60 chừng.

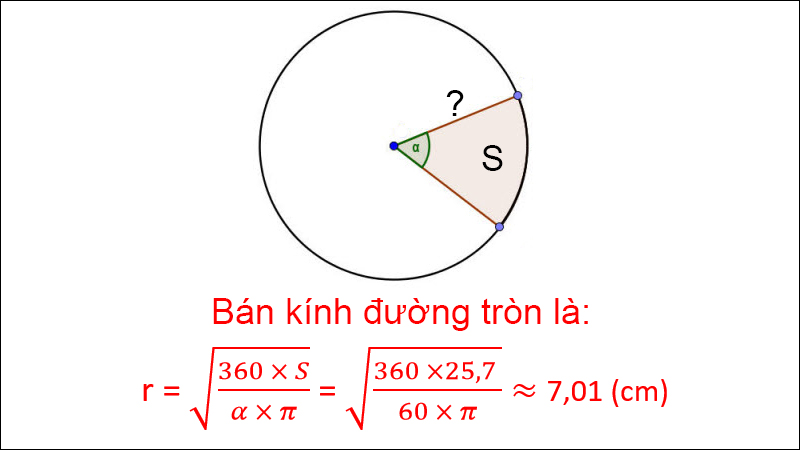
Ví dụ tính bán kính đàng tròn trĩnh lúc biết diện tích S và góc ở tâm của hình quạt

6. Những cảnh báo với câu hỏi tính bán kính hình tròn

– Dùng PC nhằm triển khai phép tắc tính mang đến nửa đường kính Khi căn bậc nhị.

– Bán kính dùng đơn vị chức năng đo chừng lâu năm. Khi ghi đáp án mang đến đơn vị chức năng của nửa đường kính cần thiết cẩn trọng, vì như thế Khi sai đơn vị chức năng rất có thể rơi rụng điểm.

– Một số bài xích nếu như ko mang đến nằm trong đơn vị chức năng thì cần triển khai phép tắc thay đổi đơn vị chức năng rồi đo lường, tách tình huống sai số.

Xem thêm: Tính thể tích của khối lăng trụ tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 6h là:

Một số khuôn mẫu Máy tính di động Flexio đang được sale bên trên Thế Giới Di Động:

Hy vọng những công thức bên trên hữu ích dành riêng cho chính mình Khi tính bán kính hình tròn trụ. Cảm ơn chúng ta vẫn theo đòi dõi và hứa tái ngộ ở những nội dung bài viết sau.

Website: https://beyeu.edu.vn