Bí quyết tính diện tích tam giác một cách nhanh chóng và chính xác nhất

Tính diện tích S tam giác là một trong câu hỏi thông thường gặp gỡ ở cung cấp đái học tập, với từng loại tam giác đem phương pháp tính diện tích S riêng rẽ. Dưới đấy là chỉ dẫn cụ thể về phong thái tính diện tích S cho tới tam giác thông thường, vuông, cân nặng và đều nhằm chúng ta cũng có thể xử lý từng câu hỏi một cơ hội đơn giản dễ dàng.

1. Cách tính diện tích S tam giác thường

Để tính diện tích S tam giác thông thường, chúng ta cũng có thể vận dụng những công thức giản dị và đơn giản sau đây:

Bạn đang xem: Bí quyết tính diện tích tam giác một cách nhanh chóng và chính xác nhất

1) SABC=12a.h$S_{ABC}=\frac{1}{2}a.h$

Dưới đấy là những bộ phận cần thiết biết:

- a là phỏng lâu năm của một trong những 3 cạnh của tam giác.

- h là chiều lâu năm của lối cao kẻ kể từ đỉnh đối lập với cạnh lòng có tính lâu năm a.

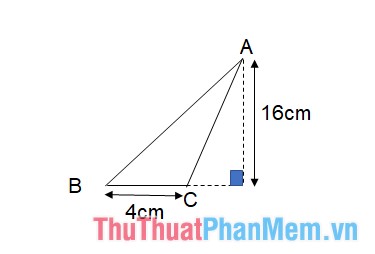
Ví dụ:  Tính diện tích S tam giác ABC với cạnh lòng BC = 4 centimet và lối cao kể từ đỉnh A là 16 centimet.

Diện tích tam giác ABC, Lúc đem lối cao ở ngoài tam giác, tính theo gót công thức: SABC=12.4.16=32(cm2)$S_{ABC}=\frac{1}{2}.4.16=32\left(c{m}^2\right)$

2) SABC=12a.b.sinC=12a.c.sinB=12b.c.sinA$S_{ABC}=\frac{1}{2}a.b.\sin C=\frac{1}{2}a.c.\sin B=\frac{1}{2}b.c.\sin A$

Diện tích tam giác là một trong nửa tích nhị cạnh nhân với sin của góc thân ái bọn chúng vô tam giác.

Ví dụ: Tính diện tích S tam giác ABC với AB = 8cm, BC = 6cm, góc B vày 60 phỏng.

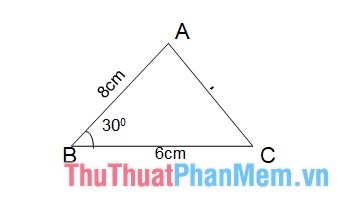
Diện tích tam giác ABC theo gót công thức:

SABC=12a.b.sinC=12.8.6.sin30=12.48.12=12(cm)$S_{ABC}=\frac{1}{2}a.b.\sin C=\frac{1}{2}.8.6.\sin 30=\frac{1}{2}.48.\frac{1}{2}=12\left(c{m}^2\right)$

3) Công thức Hê rông

Diện tích tam giác theo gót Công thức Hê rông:

Công thức Hê rông – p là nửa chu vi của tam giác, a, b, c là phỏng lâu năm của 3 cạnh vô tam giác

Ví dụ: Cho tam giác ABC với phỏng lâu năm 3 cạnh: AB=8cm, BC=6cm, AC=10cm. Tính diện tích S tam giác ABC.

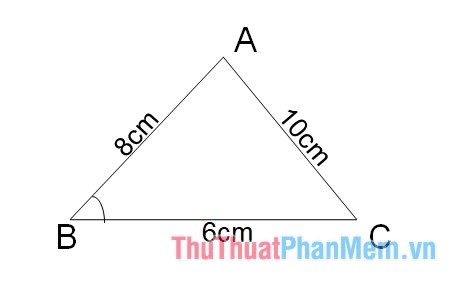
Giải:

Chu vi tam giác ABC là: PABC=(8+6+10)=24$P_{ABC}=\left(8+6+10\right)=24$ cm

Nửa chu vi tam giác là 12

Diện tích tam giác ABC theo gót công thức Hê rông:

SABC=√12(12−8)(12−6)(12−11=√288≈16,97cm2$S_{ABC}=\sqrt{12\left(12-8\right)\left(12-6\right)\left(12-11\right)}=\sqrt{288}\approx 16,97c{m}^2$

4) Diện tích tam giác ABC: SABC=p.r$S_{ABC}=p.r$

(p là nửa chu vi của tam giác, r là nửa đường kính lối tròn xoe nội tiếp tam giác)

Xem thêm: Công thức làm sữa hạt bằng máy cực nhanh

Cho tam giác ABC đem chu vi vày 28 centimet và nửa đường kính lối tròn xoe nước ngoài tiếp vày 3 centimet. Diện tích tam giác là:

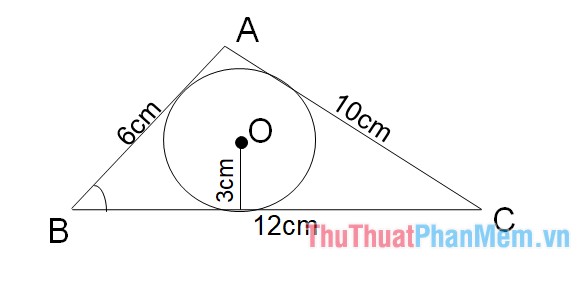
Giải

Nửa chu vi tam giác là 28/2=14cm

Diện tích tam giác ABC: SABC=p.r=14.3=42cm2$S_{ABC}=p.r=14.3=42c{m}^2$

* Chú ý Lúc tính diện tích S tam giác.

- Đối với tam giác đem độ cao ở bên phía ngoài tam giác.

- Diện tích tam giác là độ cao nhân lòng ứng.

- Khi nhị tam giác đem nằm trong độ cao hoặc độ cao đều nhau, diện tích S tỉ trọng với 2 cạnh đáy; nếu như nhị tam giác đem công cộng lòng, diện tích S tỉ trọng với 2 lối cao ứng.

2. Công thức diện tích S tam giác vuông

Diện tích tam giác vuông được xem theo gót công thức:

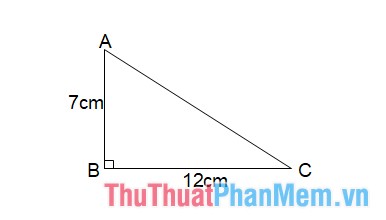
Tam giác ABC đem góc vuông bên trên B, với phỏng lâu năm cạnh AB là 7 centimet và cạnh BC là 12 centimet. Hãy tính diện tích S của tam giác ABC.

Để tính diện tích S tam giác vuông, dùng công thức sau:

Diện tích tam giác ABC vày 50% tích tích của phỏng lâu năm cạnh AB và BC:

Diện tích = (1/2) * 7 * 12 = 42 cm²

Công thức tính diện tích tam giác cân

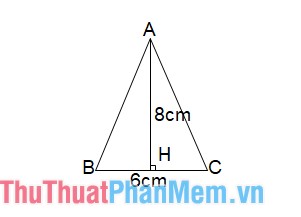
Diện tích tam giác ABC cân nặng được xem vày 50% tích tích của phỏng lâu năm cạnh lòng a và phỏng lâu năm lối cao h tương ứng:

Ví dụ: Trong tam giác ABC cân nặng bên trên A, có tính lâu năm lối cao AH là 8 centimet và cạnh lòng BC là 6 centimet.

Diện tích tam giác ABC = (1/2) * 6 * 8 = 24 cm²

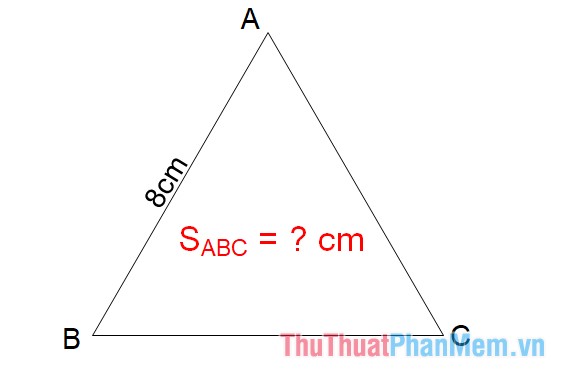
Diện tích tam giác ABC đem cạnh AB = 8 centimet là:

Công thức tính diện tích S tam giác đều:

Diện tích tam giác ABC đều với cạnh a là:

Diện tích = (8^2 * √3) / 4 = 16√3 cm²

Xem thêm: Tổng quan về ảnh hình trắng

Diện tích tam giác ABC đều với cạnh a là:

Diện tích = 16√3 cm²