Phương pháp minh chứng 2 tam giác đồng dạng giành cho học viên lớp 8 qua chuyện những cơ hội minh chứng đồng dạng và được học tập.
Hai tam giác ABC và DEF đồng dạng cùng nhau Lúc nào? Cách minh chứng rời khỏi sao?
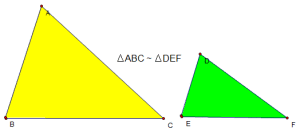
Các tình huống đồng dạng của tam giác
– Trường thích hợp đồng dạng loại nhất: 3 cạnh ứng tỉ trọng cùng nhau (c – c – c)
Bạn đang xem: Chứng minh hai tam giác đồng dạng lớp 8 - ABCD Online
Xét ∆ABC và ∆DEF, tớ sở hữu :
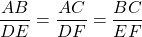
=> ∆ABC ~ ∆DEF (c – c – c)
– Trường thích hợp đồng dạng loại 2: 2 cạnh ứng tỉ trọng cùng nhau – góc xen đằm thắm nhì cạnh bởi vì nhau(c – g – c)
Xét ∆ABC và ∆DEF, tớ sở hữu :
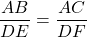
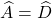
=> ∆ABC ~ ∆DEF (c – g – c)
– Trường thích hợp đồng dạng loại 3: nhì góc ứng cân nhau (g – g)
Xét ∆ABC và ∆DEF, tớ sở hữu :
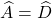
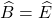
=> ∆ABC ~ ∆DEF (g – g)
Các tình huống đồng dạng của tam giác vuông
1. Định lí 1: (cạnh huyền – cạnh góc vuông)
Nếu cạnh huyền và cạnh góc vuông của tam giác này tỉ trọng với cạnh huyền và cạnh góc vuông của tam giác cơ thì nhì tam giác đồng dạng.
2. Định lí 2: (hai cạnh góc vuông)
Nếu nhì cạnh góc vuông của tam giác này tỉ trọng với nhì cạnh góc vuông của tam giác cơ thì nhì tam giác đồng dạng.
3. Định lí 3: (góc)
Nếu góc nhọn của tam giác này bởi vì góc nhọn của tam giác cơ thì nhì tam giác đồng dạng.
Bài tập dượt minh chứng tam giác đồng dạng
Muốn minh chứng 2 tam giác đồng dạng những em hoàn toàn có thể dùng những tình huống đồng dạng phía trên, quyết định lý talet (2 đường thẳng liền mạch tuy vậy song).
Theo dõi những bài bác tập dượt sở hữu tiếng giải bên dưới đây:
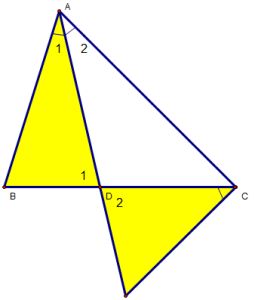
Bài 1: Cho ∆ABC (AB < AC), sở hữu AD là đàng phân giác nhập. Tại miền ngoài ∆ABC vẽ tia Cx sao mang đến 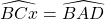 . Gọi I là phú điểm của Cx và AD. cmr :
. Gọi I là phú điểm của Cx và AD. cmr :
a) ∆ADB đồng dạng ∆CDI.
b) 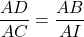
c) AD2 = AB.AC – BD.DC
Giải
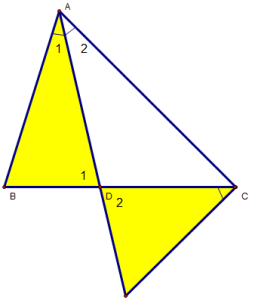 a) ∆ADB và ∆CDI , tớ sở hữu :
a) ∆ADB và ∆CDI , tớ sở hữu :
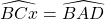 (gt)
(gt)
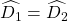 (đối đỉnh)
(đối đỉnh)
=> ∆ADB ~ ∆CDI
b) ∆ABD và ∆AIC , tớ sở hữu :
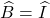 (∆ADB ~ ∆CDI)
(∆ADB ~ ∆CDI)
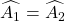 (AD là phân giác)
(AD là phân giác)
=> ∆ABD ~ ∆AIC
=> 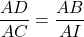
c) => AD.AI = AB.AC (1)
mà : 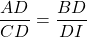 (∆ADB ~ ∆CDI )
(∆ADB ~ ∆CDI )
=> AD.DI = BD.CD (2)
từ (1) và (2) :
AB.AC – BD.CD = AD.AI – AD.DI = AD(AI – DI ) = AD.AD = AD2
Bài 2: Cho tam giác ABC vuông bên trên A, sở hữu đàng cao AH . Chứng minh những hệ thức :
a. AB2 = BH.BC và AC2 = CH.BC
b. AB2 +AC2 = BC2
c. AH2 = BH.CH
d. AH.BC = AB.AC
Giải.
 Xét nhì ∆ABC và ∆ HAC, tớ có:
Xét nhì ∆ABC và ∆ HAC, tớ có:
a. AC2 = CH.BC :
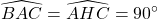
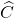 là góc cộng đồng.
là góc cộng đồng.
=> ∆ABC ~ ∆HAC (g – g)
=> 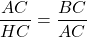
=> AC2 = CH.BC (1)
Cmtt : AB2 = BH.BC (2)
b. AB2 +AC2 = BC2
Từ (1) và (2), tớ sở hữu :
AB2 +AC2 = BH.BC + CH.BC = (BH + CH)BC = BC2
c. AH2 = BH.CH :
Xét nhì ∆HBA và ∆ HAC, tớ sở hữu :
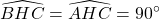
Xem thêm: Công thức cấp số nhân nâng cao | Lý thuyết + bài tập ví dụ
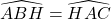 nằm trong phụ
nằm trong phụ 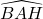
=> ∆HBA ~ ∆HAC (g – g)
=> 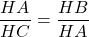
=> AH2 = BH.CH
d. AH.BC = AB.AC :
Ta sở hữu : 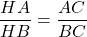 (∆ABC ~ ∆HAC)
(∆ABC ~ ∆HAC)
=> AH.BC = AB.AC.
Bài 3: Cho ∆ABC nhọn. kẻ đàng cao BD và CE. vẽ những đàng cao DF và EG của ∆ADE. Chứng minh
a) ∆ABD đồng dạng ∆AEG.
b) AD.AE = AB.AG = AC.AF
c) FG // BC
Giải
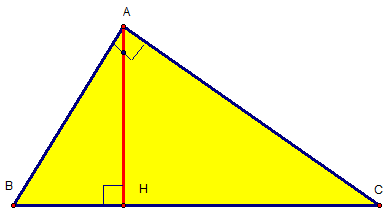 a) xét ∆ABD và ∆AEG, tớ sở hữu :
a) xét ∆ABD và ∆AEG, tớ sở hữu :
BD ⊥ AC (BD là đàng cao)
EG ⊥ AC (EG là đàng cao)
=> BD // EG
=> ∆ABD ~ ∆AGE
b) => 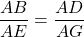
=> AD.AE = AB.AG (1)
cmtt, tớ được : AD.AE = AC.AF (2)
từ (1) và (2) suy rời khỏi :
AD.AE = AB.AG = AC.AF
c) xét ∆ABC, tớ sở hữu :
AB.AG = AC.AF (cmt)
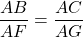
=> FG // BC (định lí hòn đảo talet)
Bài 4: Cho ∆ABC sở hữu những đàng cao BD và CE tách nhau bên trên H. Chứng minh :
a) ∆HBE đồng dạng ∆HCE.
b) ∆HED đồng dạng ∆HBC và 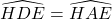
c) cho biết thêm BD = CD. Gọi M là phú điểm của AH và BC. minh chứng : DE vuông góc EM.
Giải
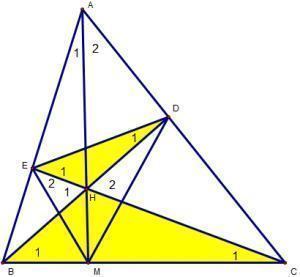 a) xét ∆HBE và ∆HCD, tớ sở hữu :
a) xét ∆HBE và ∆HCD, tớ sở hữu :
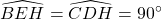 (gt)
(gt)
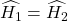 (đối đỉnh)
(đối đỉnh)
=> ∆HBE ~ ∆HCD (g – g)
b) ∆HED và ∆HBC, tớ sở hữu :
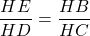 (∆HBE ~ ∆HCD)
(∆HBE ~ ∆HCD)
=> 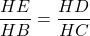
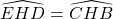 (đối đỉnh)
(đối đỉnh)
=> ∆HED ~ ∆HBC (c – g – c)
=> 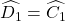 (1)
(1)
mà : Đường cao BD và CE tách nhau bên trên H (gt)
=> H là trực tâm.
=> AH ⊥ BC bên trên M.
=> 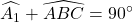
mặt khác: 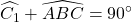
=> 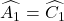 (2)
(2)
từ (1) và (2) : 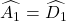
hay: 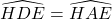
c) cmtt câu b, tớ được: 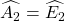 (3)
(3)
xét ∆BCD, tớ sở hữu :
DB = DC (gt)
=> ∆BCD cân nặng bên trên D
=> 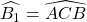
mà: 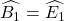 (∆HED ~ ∆HBC)
(∆HED ~ ∆HBC)
=> 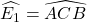
mà: 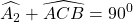
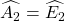 (cmt)
(cmt)
Xem thêm: Tam giác đều là gì? Diện tích, tính chất tam giác đều
=>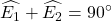
hay: 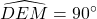
=> ED ⊥ EM.
Hình học tập 8 - Tags: đồng dạng, tam giác, tam giác đồng dạng, toán 8Tóm tắt lý thuyết Hình học tập trung học cơ sở lớp 6, 7, 8, 9

 a) ∆ADB và ∆CDI , tớ sở hữu :
a) ∆ADB và ∆CDI , tớ sở hữu : Xét nhì ∆ABC và ∆ HAC, tớ có:
Xét nhì ∆ABC và ∆ HAC, tớ có: a) xét ∆ABD và ∆AEG, tớ sở hữu :
a) xét ∆ABD và ∆AEG, tớ sở hữu : a) xét ∆HBE và ∆HCD, tớ sở hữu :
a) xét ∆HBE và ∆HCD, tớ sở hữu :