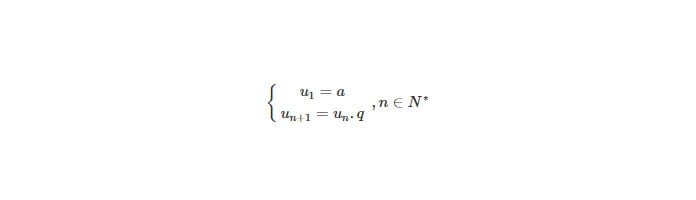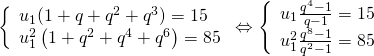Công thức cấp số nhân nâng cao | Lý thuyết + bài tập ví dụ

Công thức cấp cho số nhân: công thức tính cấp cho số nhân, công thức tính tổng cấp số nhân, tổng của cấp cho số nhân, tổng cấp cho số nhân lùi vô hạn…

Định nghĩa cấp cho số nhân

Dãy số (un) được xác lập tự $\left\{ {\begin{array}{*{20}{c}}{{u_1} = a}\\{{u_{n + 1}} = {u_n}.q}\end{array}} \right.,{\rm{ }}n \in {N^*}$ gọi là cấp cho số cộng; gọi là công bội.

Bạn đang xem: Công thức cấp số nhân nâng cao | Lý thuyết + bài tập ví dụ

$\bullet$ Số hạng loại n được mang đến tự công thức: ${u_n} = {u_1}{q^{n - 1}}$ .

$\bullet$ Ba số hạng ${u_k},{u_{k + 1}},{u_{k + 2}}$ là tía số hạng tiếp tục của cấp cho số nằm trong khi và chỉ khi $u_{k + 1}^2 = {u_k}.{u_{k + 2}}$ .

$\bullet$ Tổng số hạng thứ nhất ${S_n}$ được xác lập tự công thức :

${S_n} = {u_1} + {u_2} + ... + {u_n} = {u_1}\frac{{{q^n} - 1}}{{q - 1}}$ .

Công bội q của cấp cho số nhân

Công bội q của cấp cho số nhân $(u_{1})$ được xem tự công thức:

$q=\frac{u_{n+1}}{u_{n}}$

Ví dụ: Cho cấp cho số nhân $(u_{n})$ sở hữu $(u_{1})$ =2 , $(u_{2})$ = 4. Tính công bội q.

Lời giải: kề dụng công thức tính công bội q tớ có:

$q=\frac{u_{2}}{u_{1}}=\frac{4}{2}=2$

Số hạng tổng quát lác của cấp cho số nhân

Nếu cấp cho số nhân sở hữu số hạng đầu $(u_{1})$ và công bội q thì số hạng tổng quát lác $(u_{n})$ được xem tự công thức:

$u_{n}=u_{1}.q^{n-1}$ ới $n\geq 2$

Ví dụ: Cho cấp cho số nhân $(u_{n})$ với $(u_{1})$ = 3, $q=\frac{-1}{2}$ . Tính $(u_{7})$

Lời giải: $u_{7}=u_{1}.q^{7-1}$ =3. $(\frac{-1}{2})^{6}$ = $\frac{3}{64}$

Tổng n số hạng đầu tiên

$S_{n} = u_{1} + u_{2} + … + u_{n} = u_{1}\frac{1 - q^{n}}{1 - q} (q\neq 1)$

Nếu q = 1 thì cấp cho số nhân là $S_{n} = n.u_{1}$

Ví dụ: Cho cấp cho số nhân $(u_{n})$ biết $(u_{1})$ = 2, $(u_{3})$ = 18. Tính tổng của 10 số hạng thứ nhất.

Lời giải: Ta sở hữu $u_{3}=q^{2}.u_{1}=2.q^{2}=18$

Suy rời khỏi q = 3 hoặc q= -3

Với q =3 tớ sở hữu $S_{10}=\frac{10_{1}(1-3^10)}{1-3}$ = 59048

Với q=-3 tớ sở hữu $S_{10}=\frac{10_{1}(1-3^10)}{1+3}$ = -29524

Cấp số nhân lùi vô hạn

$(u_{n})$ sở hữu công bội q, |q|<1 được gọi là cấp cho số nhân lùi vô hạn.

Ví dụ: $\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}$ ,… là một trong những cấp cho số nhân lùi vô hạn với công bội $q=\frac{1}{2}$

Tổng của cấp cho số nhân lùi vô hạn

Cho cấp cho số nhân lùi vô hạn $(u_{n})$ sở hữu công bội q. Khi cơ tớ sở hữu tổng của cấp cho số nhân lùi vô hạn S bằng:

$S=\frac{u_{1}}{1-q}$ với |q| < 1

Ví dụ: Tính tổng của cấp cho số nhân lùi vô hạn $(u_{n})$ với $u_{n}=\frac{1}{3^{n}}$

Lời giải: Ta sở hữu $u_{1}=\frac{1}{3}$ , $u_{2}=\frac{1}{9}$ .

Suy rời khỏi $q=\frac{1}{3}$ .

Áp dụng công thức tính tổng cấp số nhân lùi vô hạn tớ có:

$S=\frac{u_{1}}{1-q}$

$S=\frac{\frac{1}{3}}{1-\frac{1}{3}}=\frac{1}{2}$

Bài luyện minh họa cấp cho số nhân

Vấn đề 1: Xác tấp tểnh cấp cho số và xác nguyên tố của cấp cho số nhân

Phương pháp:

$\bullet$ Dãy số $({u_n})$ là một trong những cấp cho số nhân $\Leftrightarrow \frac{{{u_{n + 1}}}}{{{u_n}}} = q$ ko tùy thuộc vào n và là công bội.

$\bullet$ Ba số theo đuổi trật tự cơ lập trở thành cấp cho số nhân $\Leftrightarrow ac = {b^2}$ .

$\bullet$ Để xác lập một cấp cho số nhân, tớ cần thiết xác lập số hạng đầu và công bội. Do cơ, tớ thông thường biểu diễn thuyết thiết của vấn đề qua chuyện ${u_1}$ và .

Ví dụ 1:

Cho cấp cho số nhân (un) sở hữu những số hạng không giống ko, dò thám ${u_1}$ biết:

Xem thêm: Tìm hiểu về nguyên hàm cos bình x và ứng dụng trong toán học

a) $\left\{ {\begin{array}{*{20}{c}}{{u_1} + {u_2} + {u_3} + {u_4} = 15}\\{u_1^2 + u_2^2 + u_3^2 + u_4^2 = 85}\end{array}} \right.$

b) $\left\{ {\begin{array}{*{20}{c}}{{u_1} + {u_2} + {u_3} + {u_4} + {u_5} = 11}\\{{u_1} + {u_5} = \frac{{82}}{{11}}}\end{array}} \right.$

Hướng dẫn:

a) Ta có: $\left\{ \begin{array}{l}{u_1}(1 + q + {q^2} + {q^3}) = 15\\u_1^2\left( {1 + {q^2} + {q^4} + {q^6}} \right) = 85\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1}\frac{{{q^4} - 1}}{{q - 1}} = 15\\u_1^2\frac{{{q^8} - 1}}{{{q^2} - 1}} = 85\end{array} \right.$

$\Rightarrow {\left( {\frac{{{q^4} - 1}}{{q - 1}}} \right)^2}\left( {\frac{{{q^2} - 1}}{{{q^8} - 1}}} \right) = \frac{{45}}{{17}} \Leftrightarrow \frac{{({q^4} - 1)(q + 1)}}{{(q - 1)({q^4} + 1)}} = \frac{{45}}{{17}} \Leftrightarrow \left[ \begin{array}{l}q = 2\\q = \frac{1}{2}\end{array} \right.$

Từ cơ tớ tìm kiếm được ${u_1} = 1,{u_1} = 8$ .

b) Ta có: $\left\{ \begin{array}{l}{u_1}\left( {1 + q + {q^2} + {q^3} + {q^4}} \right) = 11\\{u_1}(1 + {q^4}) = \frac{{82}}{{11}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1}q(1 + q + {q^2}) = \frac{{39}}{{11}}\\{u_1}(1 + {q^4}) = \frac{{82}}{{11}}\end{array} \right.$

$\Rightarrow \frac{{{q^4} + 1}}{{{q^3} + {q^2} + q}} = \frac{{82}}{{39}} \Leftrightarrow q = 3,q = \frac{1}{3}$ .

Ví dụ 2:

Cho cấp cho số nhân $({u_n})$ thỏa: $\left\{ \begin{array}{l}{u_4} = \frac{2}{{27}}\\{u_3} = 243{u_8}\end{array} \right.$ .

a) Viết năm số hạng đầu của cấp cho số.

b) Tính tổng 10 số hạng đầu của cấp cho số.

c) Số $\frac{2}{{6561}}$ là số hạng loại từng nào của cấp cho số?

Hướng dẫn:

Gọi là công bội của cấp cho số. Theo fake thiết tớ có:

$\left\{ \begin{array}{l}{u_1}{q^3} = \frac{2}{{27}}\\{u_1}{q^2} = 243.{u_1}{q^7}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1}{q^3} = \frac{2}{{27}}\\{q^5} = \frac{1}{{243}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}q = \frac{1}{3}\\{u_1} = 2\end{array} \right.$

a) Năm số hạng đầu của cấp cho số là: ${u_1} = 2,{u_2} = \frac{2}{3},{u_3} = \frac{2}{9};{u_4} = \frac{2}{{27}},{u_5} = \frac{2}{{81}}$ .

b) Tổng 10 số hạng đầu của cấp cho số

${S_{10}} = {u_1}\frac{{{q^{10}} - 1}}{{q - 1}} = 2.\frac{{{{\left( {\frac{1}{3}} \right)}^{10}} - 1}}{{\frac{1}{3} - 1}} = 3\left[ {1 - {{\left( {\frac{1}{3}} \right)}^{10}}} \right] = \frac{{59048}}{{19683}}$ .

c) Ta có: ${u_n} = \frac{2}{{{3^{n - 1}}}} \Rightarrow {u_n} = \frac{2}{{6561}} \Leftrightarrow {3^{n - 1}} = 6561 = {3^8} \Rightarrow n = 9$

Vậy $\frac{2}{{6561}}$ là số hạng loại 9 của cấp cho số.

Vấn đề 3: Tìm ĐK nhằm mặt hàng số lập trở thành cấp cho số nhân

Phương pháp: theo đuổi trật tự cơ lập trở thành CSN $\Leftrightarrow ac = {b^2}$ .

Ví dụ 1: Tìm biết $1,{x^2},6 - {x^2}$ lập trở thành cấp cho số nhân.

Hướng dẫn:

Ta có: $1,{x^2},6 - {x^2}$ lập trở thành cấp cho số nhân $\Leftrightarrow {x^4} = 6 - {x^2} \Leftrightarrow x = \pm \sqrt 2 .$

Ví dụ 2: Tìm biết:

a) Các số lập trở thành cấp cho số cộng và những số

${\left( {y - 1} \right)^2},xy - 1,{\left( {x + 1} \right)^2}$ lập trở thành cấp cho số nhân.

b) Các số lập trở thành cấp cho số nằm trong và những số $x + \frac{5}{3}y,hắn - 1,2x - 3y$ lập trở thành cấp cho số nhân.

Hướng dẫn:

a) Ta sở hữu hệ: $\left\{ \begin{array}{l}x + 5y + 8x + hắn = 2(5x + 2y)\\{(x + 1)^2}{(y - 1)^2} = {(xy - 1)^2}\end{array} \right.$ giải hệ này tớ dò thám được

$(x;y) = \left( { - \sqrt 3 ; - \frac{{\sqrt 3 }}{2}} \right);\left( {\sqrt 3 ;\frac{{\sqrt 3 }}{2}} \right)$ .

b) Ta sở hữu hệ: $\left\{ \begin{array}{l}x + 6y + 8x + hắn = 2(5x + 2y)\\(x + \frac{5}{3}y)(2x - 3y) = {(y - 1)^2}\end{array} \right.$ giải hệ này tớ dò thám được

$(x;y) = \left( { - 3; - 1} \right);\left( {\frac{3}{8};\frac{1}{8}} \right)$ .

Xem thêm: Công thức tính Diện tích hình vuông, hình chữ nhật, hình tròn, hình tam giác...

Mời chúng ta coi tăng video clip bài bác giảng về “Cấp số nhân”:

Trên đó là nội dung bài viết công thức cấp cho số nhân, chúc chúng ta thực hiện bài bác tốt!

Công thức cấp số nhân nâng cao | Lý thuyết + bài tập ví dụ

Định nghĩa cấp cho số nhân

Công bội q của cấp cho số nhân

Số hạng tổng quát lác của cấp cho số nhân

Tổng n số hạng đầu tiên

Cấp số nhân lùi vô hạn

Tổng của cấp cho số nhân lùi vô hạn

Bài luyện minh họa cấp cho số nhân

BÀI VIẾT NỔI BẬT

Tổng hợp kiến thức Vật lý 11 theo chương trình mới

Vấn đề đường trung tuyến trong tam giác vuông, tam giác cân, tam giác đều (cách giải + bài tập).

Cách giải bài dạng: Tìm điều kiện để phương trình có nghiệm. Tìm nghiệm của phương trình bậc hai Toán lớp 9 | Chuyên đề toán 9

Hình ảnh Doraemon chibi, Doraemon cute đẹp nhất

Tìm hiểu về nguyên hàm của sin bình x trong toán học