Cảm ứng từ là gì? Công thức tính và áp dụng trong thực tế

Cảm ứng kể từ là gì?

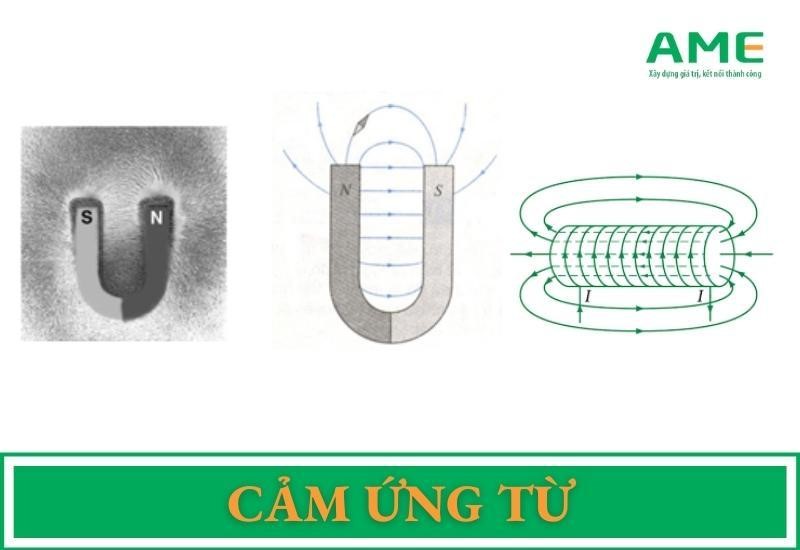
Cảm ứng từ (ký hiệu B) là đại lượng được bố trí theo hướng bên trên một điểm nhập kể từ ngôi trường, biểu thị phỏng mạnh yếu hèn của kể từ ngôi trường, vị trí hướng của kể từ ngôi trường và lực thuộc tính của lực kể từ. Độ cảm ứng từ được đo vị thương thân mật số lực kể từ thuộc tính lên thừng dẫn đem dòng sản phẩm năng lượng điện được bịa vuông góc với đàng cảm ứng từ bên trên điểm cơ.

Bạn đang xem: Cảm ứng từ là gì? Công thức tính và áp dụng trong thực tế

Véc tơ của cảm ứng từ B sở hữu là phương tiếp tuyến với đàng mức độ bên trên điểm cơ sở hữu chiều kể từ cực kỳ phái mạnh thanh lịch cực kỳ bắc của nam châm hút từ.

Quy tắc bàn tay phải

Để xác lập chiều của những đàng mức độ kể từ nhập ống thừng dẫn hình trụ, người tao vận dụng bám theo quy tắc bàn tay nên. Quy tắc này được tuyên bố như sau: Nắm bàn tay nên theo hướng của vòng thừng, chiều kể từ cổ tay cho tới ngón loại trùng chiều dòng sản phẩm năng lượng điện trải qua cuộn thừng, ngón loại choãi đi ra 90 phỏng chỉ chiều những đàng mức độ kể từ trong tim ống thừng.

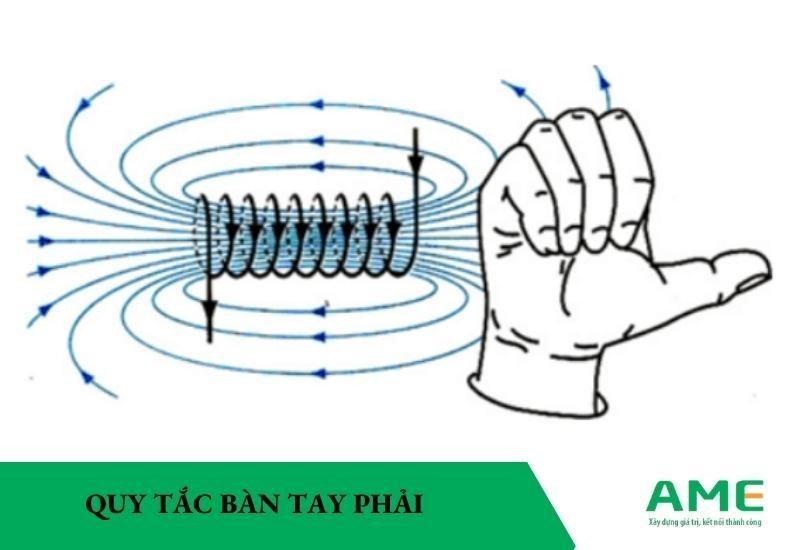
Quy tắc bàn tay phải

Đơn vị cảm ứng từ

Cảm ứng từ sở hữu đơn vị chức năng là Tesla (T) với cùng một T là khuôn khổ của cảm ứng từ của vòng thừng dẫn kín sở hữu diện tích S mặt mũi phẳng lì chắn được bên phía trong là 1m2. Nếu kể từ thông hạ xuống 0 thì nhập 1s  sẽ tạo nên đi ra suất năng lượng điện động 1V. Tên đơn vị chức năng cảm ứng từ được bịa bám theo ngôi nhà bác bỏ học tập người Áo Nikola Tesla.

Công thức tính cảm ứng từ

Để tính cảm ứng từ, tao sở hữu công thức sau: B = F/I.l

Trong đó:

• B: Cảm ứng từ
• F: Lực từ
• I: Cường phỏng dòng sản phẩm năng lượng điện qua chuyện dây

Áp dụng những công thức tính cảm ứng từ cho tới từng môi trường

Bên cạnh dùng công thức cộng đồng nhằm tính cảm ứng từ thì trong số tình huống không giống nhau sẽ có được công thức tính riêng rẽ giản dị và đơn giản, nhanh gọn rộng lớn.

Tính kể từ ngôi trường cho tới thừng dẫn lâu năm vô hạn

Xác ấn định cảm ứng từ vector B bên trên điểm M cơ hội thừng dẫn một quãng r với độ mạnh dòng sản phẩm năng lượng điện I. Ta xét vector B như sau:

• Điểm đặt: điểm M
• Phương: Vuông góc với mặt mũi phẳng lì chứa chấp điểm M và thừng dẫn
• Chiều: Sử dụng quy tắc bàn tay nên nhằm xác định
• Độ lớn: Bm = (2.10^-7. I)/Rm

Trong đó:

• Bm: Cảm ứng kể từ bên trên điểm M
• R: Khoảng cơ hội kể từ điểm xét cho tới thừng dẫn
• I: Cường phỏng dòng sản phẩm năng lượng điện cút qua

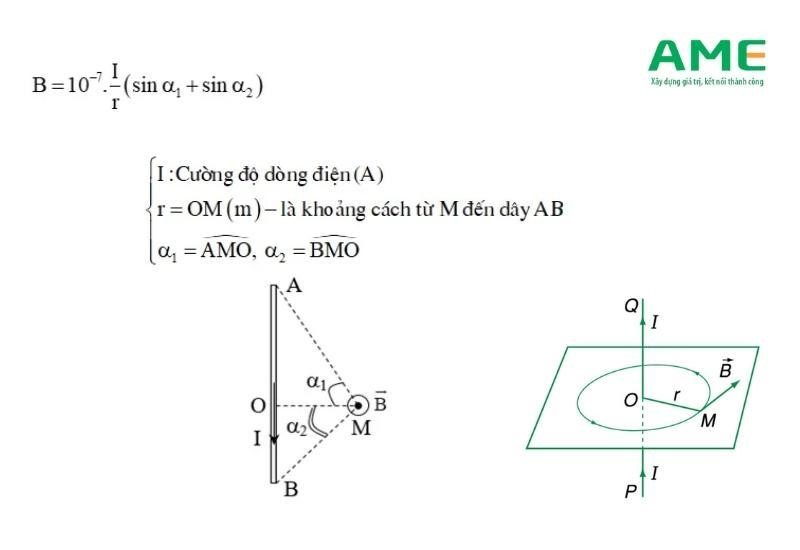
Đối với thừng sở hữu chiều lâu năm hữu hạn thì cảm ứng từ tự thừng dẫn tạo nên bên trên điểm M sẽ tiến hành tính bám theo công thức:

Xem thêm: Ảnh gái xinh che mặt

Tính kể từ ngôi trường cho tới thừng dẫn lâu năm vô hạn

Ví dụ: Xác ấn định cảm ứng từ tự dòng sản phẩm năng lượng điện trong một thừng dẫn lâu năm trực tiếp vô hạn sở hữu I = 10A bên trên điểm M cơ hội thừng 5cm. kề dụng công thức tao có: Bm = (2.10-7. 10)/0.05= 4.10^-5 (T)

Tính kể từ ngôi trường dòng sản phẩm năng lượng điện tròn

Để tính chạm màn hình vector B bên trên tâm O của vòng thừng dẫn nửa đường kính R, dòng sản phẩm năng lượng điện I, tao xác lập như sau:

• Điểm đặt: Tâm O của cuộn dây
• Phương: Vuông góc với mặt mũi phẳng lì vòng dây
• Chiều: Xác ấn định vị quy tắc bàn tay phải
• Độ lớn: Bo = (2π.10^-7. I)/R

Trong đó:

• Bo: Cảm ứng kể từ bên trên điểm O
• R: Khoảng cơ hội kể từ điểm xét cho tới thừng dẫn
• I: Cường phỏng dòng sản phẩm năng lượng điện cút qua

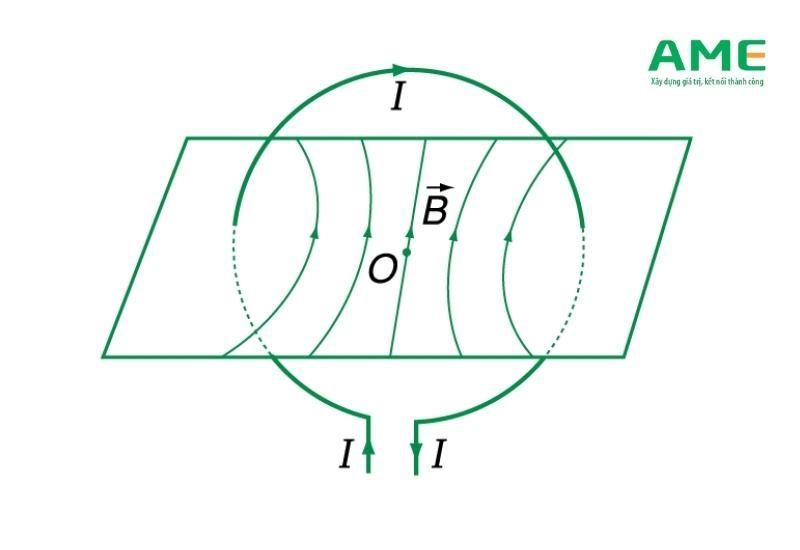
Tính kể từ ngôi trường dòng sản phẩm năng lượng điện tròn

Ví dụ: Xác ấn định cảm ứng từ tự dòng sản phẩm năng lượng điện trong một khuông thừng sở hữu nửa đường kính 5cm, khuông thừng có một vòng và I = 5A. kề dụng công thức tao có:

Bm = (2π.10^-7. 5)/0.05= 2π.10^-5 (T)

Tính kể từ ngôi trường ống dây

Xác định cảm ứng từ B bên trên một điểm bất kì mặt mũi trong tim ống thừng dẫn sở hữu độ mạnh dòng sản phẩm năng lượng điện I. Ta có:

• Điểm đặt: Tại điểm xét
• Phương: Song tuy nhiên với trục ống thừng dẫn
• Chiều: Sử dụng quy tắc tóm bàn tay phải
• Độ lớn: B = (4π.10-7. I.N)/R = 4π.10^-7. I.n

Trong đó:

Xem thêm: Lý thuyết và hướng dẫn giải bài tập về Góc ở tâm. Số đo cung - HOCMAI

• B: Cảm ứng kể từ bên trên điểm
• N: Số vòng thừng dẫn
• L: Chiều lâu năm ống dây
• I: Cường phỏng dòng sản phẩm năng lượng điện cút qua

Ví dụ: Tính cảm ứng từ B nhập cuộn thừng sở hữu độ mạnh I=10A, cuộn thừng sở hữu 5 vòng thừng, khoảng cách bên trên điểm xét cho tới cuộn thừng là 0.05m. Ta có:

B =  (4π.10^-7 I.N)/R = 4π.10^-7.10×5/0.05 = 8π.10^-4  (T)

Như vậy, bên trên đó là vấn đề tiết về cảm ứng từ cũng tựa như những công thức tính rõ ràng cảm ứng từ vào cụ thể từng tình huống. Hãy kế tiếp bám theo dõi AME Group trong số nội dung bài viết tiếp sau nhằm cảm nhận được những vấn đề hữu ích nhất!