beyeu
beyeu
Trang chủ Giáo Dục Công thức tính diện tích hình chóp

Công thức tính diện tích hình chóp

Diện tích hình chóp bao gồm với diện tích S xung xung quanh và diện tích S toàn phần. Bài ghi chép tiếp sau đây tiếp tục trình làng với chúng ta công thức tính diện tích S hình chóp, tính diện tích S xung xung quanh và diện tích S toàn phần của hình chóp đều, hình chóp tứ giác đều.

Hình chóp

Bạn đang xem: Công thức tính diện tích hình chóp

1. Công thức tính diện tích S xung xung quanh hình chóp

Hình chóp đều

Sxq=p.d

Sxq là diện tích S xung quanh

p là nửa chu vi đáy

d là trung đoạn của hình chóp đều

Hình chóp tứ giác đều

Sxq = Tổng diện tích S những mặt mày mặt (Tổng diện tích S của 4 tam giác)


2. Công thức tính diện tích S toàn phần của hình chóp

Stp = Sxq + S đáy

3. Bài tập dượt về diện tích S hình chóp 

Bài 1: 

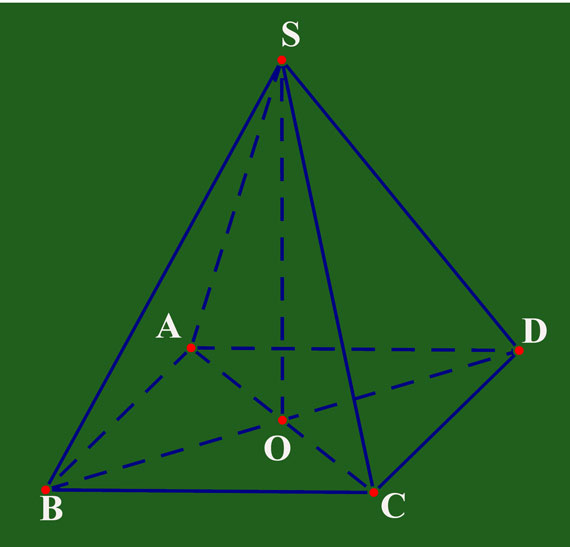
Cho hình chóp SABCD lòng là hình vuông vắn với cạnh nhiều năm 8 centimet, phỏng nhiều năm những cạnh mặt mày vày 10 centimet. Hãy tính diện tích S xung xung quanh, diện tích S toàn phần của hình chóp SABCD.

Hình chóp SABCD

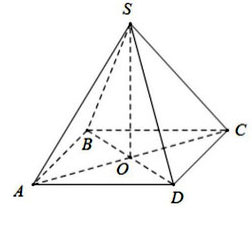
Giải:

Nửa chu vi của hình vuông vắn ABCD bằng:

P=\frac{AB+BC+CD+AD}{2}\ =\ \frac{8+8+8+8}{2}=16

BD=AC=\sqrt{8^{2\ }+8^2}=8\sqrt{2}cm

=> AO = BO = CO = DO = 4\sqrt{2} cm

Diện tích xung xung quanh của hình chóp đều:

Sxq=p.d=p.OB=16.4\sqrt{2}=64\sqrt{2}\ cm^2

Diện tích toàn phần của hình chóp đều là:

Xem thêm: Tất cả công thức lý 11 học kì 1 : Những kiến thức cơ bản mà bạn cần nắm vững

Stp=Sxq+SABCD=64\sqrt{2}+82=64+64\sqrt{2}cm^2

Bài 2: Cho hình chóp tam giác đều sở hữu cạnh lòng vày a và độ cao vày 2a. Tính diện tích S toàn phần của hình chóp tam giác đều?

Tính diện tích S của hình chóp tam giác đều

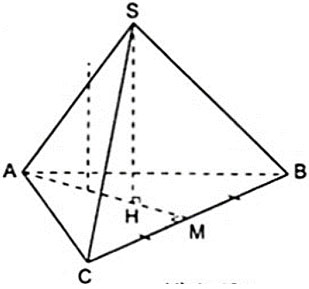
Giải:

Hình chóp tam giác đều S.ABC với AB = AC = BC = a và SH = 2a.

Gọi M là trung điểm của BC. Vì ABC là tam giác đều nên AM một vừa hai phải là đàng trung tuyến, một vừa hai phải là đàng cao, một vừa hai phải là đàng phân giác nên AM ⊥ BC và HM = 1/3AM.

Áp dụng toan lý Pytago vô tam giác vuông ABM vuông bên trên M tớ được:

AB^2=BM^2+AM^2⇒a^2=(\frac{a}{2})^2+AM^2

AM^2=\left(\frac{a\sqrt{3}}{2}\right)^2\ =>\ AM=\frac{a\sqrt{3}}{2}

Do đó

HM=\frac{a\sqrt{3}}{6}

Áp dụng toan lí Pytago vô tam giác vuông SHM vuông bên trên H, tớ có:

SM^2=HM^2+SH^2⇒SM^2=\left(\frac{a\sqrt{3}}{6}\right)^2+(2a)^2

SM\ ^{2\ }=\ \left(\frac{7a\sqrt{3}}{6}\right)^{2\ }=>\ SM\ =\ \frac{7a\sqrt{3}}{6}

Diện tích toàn phần của hình chóp tam giác đều SABC là:

Sxq\ =\ \frac{3a}{2}\frac{7a\sqrt{3}}{6}=\ \frac{7a^2\sqrt{6}}{4}

Xem thêm: Hình ảnh Nền Tr%e1%ba%afng Tinh Khi%e1%ba%bft, Tr%e1%ba%afng Tinh Khi%e1%ba%bft Vector Nền Và Tập Tin Tải về Miễn Phí | Pngtree

Sd=\frac{1}{2}a\ \frac{a\sqrt{3}}{2}=\ a^2\frac{\sqrt{3}}{4}

=> Stp=\frac{7a^2\sqrt{6}}{4}+\frac{a^2\sqrt{3}}{4}\ =2a^2\sqrt{3}

Các chúng ta có thể lần hiểu tăng về công thức tính thể tích khối chóp, chu vi hình chóp.

BÀI VIẾT NỔI BẬT

Bài tập phương trình hóa học lớp 8

Bài tập phương trình hóa học lớp 8 được biến soạn có đáp án, hy vọng tài liệu giúp ích cho các bạn học sinh củng cố luyện tập biết cách cân bằng phường trình phản ứng.

Tìm hiểu về nguyên hàm của sin bình x trong toán học

Chủ đề nguyên hàm của sin bình x Nguyên hàm của sin bình x là một khái niệm quan trọng trong toán học. Bằng cách sử dụng các công thức hạ bậc và các quy tắc tích phân, chúng ta có thể tính được giá trị của nguyên hàm này. Điều này giúp chúng ta hiểu rõ hơn về hàm số sin và áp dụng nó trong các bài toán tính toán.