beyeu
beyeu
Trang chủ Giáo Dục Cách viết phương trình tiếp tuyến của đường tròn đơn giản - kiến thức Toán 10

Cách viết phương trình tiếp tuyến của đường tròn đơn giản - kiến thức Toán 10

Phương trình tiếp tuyến phố tròn trặn là phần kiến thức và kỹ năng toán 10 thân thuộc và thông thường gặp gỡ trong những kỳ ganh đua. Trong nội dung bài viết tại đây, VUIHOC tiếp tục với những em học viên ôn luyện lý thuyết tổng quan liêu về phương trình tiếp tuyến, chỉ dẫn cơ hội viết phương trình tiếp tuyến phố tròn trặn và rèn luyện với cỗ bài xích luyện trắc nghiệm tinh lọc.

1. Lý thuyết cộng đồng về phương trình tiếp tuyến phố tròn

Bạn đang xem: Cách viết phương trình tiếp tuyến của đường tròn đơn giản - kiến thức Toán 10

Phương trình tiếp tuyến của đàng tròn

Phương trình đàng tròn trặn đem tâm I (a; b), nửa đường kính R  là:

(x - a)^2 + (y - b)^2 = R^2

Phương trình đàng tròn trặn (x - a)^2 + (y - b)^2 = R^2 hoàn toàn có thể ghi chép bên dưới dạng:

x^2 + y^2 - 2ax - 2by + c = 0. Trong đó: c = a^2 + b^2 - R^2

Điều khiếu nại nhằm phương trình x^2 + y^2 - 2ax - 2by + c = 0 là phương trình đàng tròn trặn (C) Khi và chỉ Khi a^2 + b^2 - c > 0.

Khi cơ đàng tròn trặn (C) đem tâm I (a; b) và nửa đường kính R = a^2 + b^2 - c

Đăng ký tức thì sẽ được những thầy cô ôn luyện và kiến thiết quãng thời gian học tập tập THPT vững vàng vàng

2. Phương trình tiếp tuyến của đàng tròn

2.1. Lý thuyết

Cho điểm 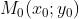M_0 (x_0; y_0) phía trên đàng tròn trặn (C), tâm I (a; b). Gọi Δ là tiếp tiếp của (C) bên trên M_0.

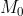Ta có:

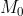M_0 thuộc Δ và vectơ 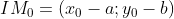IM_0 = (x_0 - a; y_0 - b) là vectơ pháp tuyến của Δ. 

Do cơ phương trình của Δ là:

(x_0 - a)(x - x_0) + (y_0 - b) (y - y_0) = 0 (1)

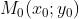Vậy phương trình (1) là phương trình tiếp tuyến của đàng tròn trặn (x - a)^2 + (y - b)^2 = R^2  bên trên điểm M_0 (x_0; y_0) phía trên đàng tròn trặn.

Phương trình tiếp tuyến của đường tròn trặn (C)

2.2. Phương pháp giải

Dạng 1: Viết phương trình tiếp tuyến của đàng tròn trặn bên trên 1 điều nằm trong đàng tròn

Ta người sử dụng công thức tách song tọa độ:

- Nếu phương trình đàng tròn trặn là: x^2 + y^2 - 2ax - 2by + c = 0 thì phương trình tiếp tuyến là: xx_0 + yy_0 - a(x + x_0) - b(y + y_0) + c = 0

- Nếu công thức đàng tròn trặn là: (x - a)^2 + (y - b)^2 = R^2 thì phương trình tiếp tuyến là: (x - a)(x_0 - a) + (y - b)(y_0 - b) = R^2

Dạng 2: Viết phương trình tiếp tuyến của đàng tròn trặn bên trên 1 điều ngoài đàng tròn

Viết phương trình của đường thẳng liền mạch (Δ) qua quýt 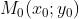M_0 (x_0; y_0):

y - y_0 = m(x - x_0) \Leftrightarrow mx - nó - mx_0 + y_0 = 0 (1)

Cho khoảng cách kể từ tâm I của đàng tròn trặn cho tới đường thẳng liền mạch (Δ) = R, tao tính được m; thay cho m nhập (1) tao được phương trình tiếp tuyến.

*Chú ý: Ta luôn luôn tìm kiếm được hai tuyến đường tiếp tuyến.

Dạng 3: Viết phương trình tiếp tuyến tuy vậy song với phương mang đến sẵn đem thông số góc k

Phương trình của  (Δ) đem dạng: nó = kx + m (m ko biết) ⇔ kx - nó +m = 0

Cho khoảng cách kể từ tâm I cho tới (D) bởi vì R, tao tìm kiếm được m.

*Chú ý: Ta luôn luôn tìm kiếm được hai tuyến đường tiếp tuyến.

Tham khảo tức thì cỗ tư liệu tổ hợp hoàn toàn cỗ kiến thức và kỹ năng và cách thức giải từng dạng bài xích luyện Toán ganh đua THPT  

2.3. Ví dụ bài xích luyện viết phương trình tiếp tuyến của đàng tròn

Ví dụ 1: Cho đàng tròn trặn (C): (x - 1)^2 + (y + 2)^2 = 2. Viết phương trình tiếp tuyến d của (C) bên trên điểm A(3;-4)

Hướng dẫn giải:

Đường tròn trặn (C) đem tâm I(1; -2)

Do đường thẳng liền mạch d xúc tiếp với đàng tròn trặn bên trên điểm A(3; - 4) nên đường thẳng liền mạch d vuông góc với đường thẳng liền mạch IA.

- Phương trình đường thẳng liền mạch (d): 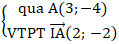Viết phương trình tiếp tuyến của đàng tròn trặn bên trên 1 điều, chuồn qua một điểm - Toán lớp 10

⇒ Phương trình (d) là: 2(x - 3) - 2(y + 4) = 0

⇔ (d) : 2x - 2y - 14 = 0 hoặc x - nó - 7 = 0

Ví dụ 2: Viết phương trình tiếp tuyến ∆ của đàng tròn trặn (C): x^2+ y^2 - 4x - 4y + 4 = 0, biết tiếp tuyến trải qua điểm B(4; 6) .

Hướng dẫn giải:

- Đường tròn trặn (C) đem tâm I( 2; 2) và nửa đường kính R = 22+ 22-4 = 2

- Tiếp tuyến ∆: Viết phương trình tiếp tuyến của đàng tròn trặn bên trên 1 điều, chuồn qua một điểm - Toán lớp 10

⇒ Phương trình ∆: a(x - 4) + b(y - 6) = 0 hoặc ax + by - 4a - 6b = 0 (*)

- Do ∆ là tiếp tuyến của đàng tròn trặn ( C) nên $d(I; ∆) = R$

⇔  |2a+2b-4a-6b| a^2+ b^2= 2 \Leftrightarrow |- 2a - 4b| = 2 a^2+ b^2

⇔ |a + 2b| = a^2+ b^2 \Leftrightarrow a^2+ 4ab + 4b^2 = a^2 + b^2

⇔ 4ab + 3b2 = 0

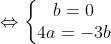
\Leftrightarrow \left\{\begin{matrix} b=0\\ 4a=-3b\end{matrix}\right.

- Nếu b=0: lựa chọn a = 1 thay cho nhập (*) tao được ∆: x - 4 = 0.

- Nếu 4a=-3b: chọn a=3 thì b=-4 thay cho nhập (*) tao được: 3x - 4y + 12 = 0

Vậy đem nhì tiếp tuyến thỏa mãn nhu cầu là x - 4 = 0 và 3x - 4y + 12 = 0

Ví dụ 3: Cho đàng tròn trặn (x - 3)^2 + (y+1)^2 = 5. Phương trình tiếp tuyến của (C) tuy vậy song với đường thẳng liền mạch d : 2x + nó + 7 = 0 là?

Hướng dẫn giải:

Do tiếp tuyến cần thiết lần tuy vậy song với đường thẳng liền mạch d: 2x + nó + 7 = 0 nên

phương trình tiếp tuyến đem dạng ∆: 2x + nó + m = 0 với m ≠ 7 .

Đường tròn trặn (C) đem tâm I( 3; -1) và nửa đường kính R=5

Đường trực tiếp xúc tiếp với đàng tròn trặn (C) Khi :

d( I , ∆) = R ⇔ |2.3-1+m|5= 5 ⇔ |5 + m| = 5

⇔ Viết phương trình tiếp tuyến của đàng tròn trặn ví dụ 3 

Vậy ∆1 : 2x + nó = 0 , ∆2 : 2x + nó - 10 = 0

3. Bài luyện tập viết phương trình tiếp tuyến của đàng tròn

Câu 1: Cho đàng tròn trặn (C) :(x - 3)^2 + (y-1)^2 = 10. Phương trình tiếp tuyến của đàng tròn (C) bên trên điểm A(4;4) là

Xem thêm: Công thức tính nửa chu vi hình chữ nhật và bài tập có lời giải từ A – Z

A. x - 3y + 8 = 0.       B. x + 3y – 16 = 0.    

C. 2x - 3y + 5 = 0 .    D. x + 3y - 16 = 0.

Câu 2: Viết phương trình tiếp tuyến của đàng tròn trặn (C): x^2 + y^2 - 4x - 4y + 4 = 0, biết tiếp tuyến trải qua điểm B(4; 6):

A. x - 4 = 0 hoặc 3x + 4y - 36 = 0     B. x - 4 = 0 hoặc nó - 6 = 0.

C. nó - 6 = 0 hoặc 3x + 4y - 36 = 0     D. x - 4 = 0 hoặc 3x - 4y + 12 = 0

Câu 3: Phương trình tiếp tuyến d của đàng tròn trặn (C): (x+2)^2 + (y+2)^2 = 25 bên trên điểm M(2;1) là:

A. d: -y + 1 = 0    B. d: 4x + 3y + 14 = 0

C. d: 3x - 4y - 2 = 0    D. d: 4x + 3y - 11 = 0

Câu 4: Cho đàng tròn trặn (C): (x-1)^2 + (y+2)^2 = 2. Viết phương trình tiếp tuyến d của (C) bên trên điểm A(3;-4) .

A. d: x + nó + 1 = 0      B. d: x - 2y - 11 = 0

C. d: x - nó - 7 = 0        D. d: x - nó + 7 = 0

Câu 5: Cho đàng tròn trặn (C): (x+1)^2 + (y-1)^2 = 25 và điểm M(9;-4). Gọi ∆ là tiếp tuyến của (C), biết ∆ trải qua M và ko tuy vậy song với những trục tọa chừng. Khi cơ khoảng cách kể từ điểm P(6; 5) cho tới ∆ bằng:

A. 2                                B. 3                                     C. 4                                   D. 5

Câu 6: Có từng nào đường thẳng liền mạch trải qua gốc tọa chừng O và xúc tiếp với đàng tròn

(C): x^2 + y^2 - 2x + 4y - 11 = 0?

A. 0.                              B. 2.                                      C. 1.                                 D. 3.

Câu 7: Viết phương trình tiếp tuyến của đàng tròn trặn (C): (x-1)^2+(y+2)^2=8, biết tiếp tuyến trải qua điểm A(5; -2):

A. x - 5 = 0 .                               B. x + nó - 3 = 0 hoặc x - nó 7 = 0.

C. x- 5= 0 hoặc x + nó - 3 = 0 .    D. nó + 2 = 0 hoặc x - nó - 7 = 0 .

Câu 8: Cho đàng tròn trặn (C) đem tâm I(1;3), nửa đường kính $R= 5^2$. Lập phương trình tiếp tuyến của đàng tròn trặn bên trên điểm M biết điểm M nằm trong đường thẳng liền mạch d: 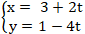Viết phương trình tiếp tuyến của đàng tròn trặn bài xích luyện 8 và tọa chừng M nguyên?

A. x + 2y + 3 = 0                 B. 2x + 5y + 21 = 0

C. 2x - 3y - 19 = 0               D. Đáp án khácCâu 9: Phương trình tiếp tuyến của đàng tròn trặn (C): x^2 + y^2-3x-y= 0 bên trên điểm N(1;-1) là:

A. d: x + 3y - 2 = 0              B. d: x - 3y + 4 = 0

C. d: x - 3y - 4 = 0              D. d: x + 3y + 2 = 0

Câu 10: Cho đàng tròn trặn (C): x^2 + y^2 - 2x + 8y - 23 = 0 và điểm M(8;-3) . Độ lâu năm đoạn tiếp tuyến của (C) xuất phát điểm từ M là :

A. 10                      B. 210                        C. 102                            D. 10

Câu 11: Cho đàng tròn trặn (C) : x^2+y^2-3x-y=0. Phương trình tiếp tuyến của đàng tròn (C) bên trên M(1;-1) là:

A. x + 3y - 1 = 0               B. 2x - 3y + 1 = 0                C. 2x - nó + 4 = 0                D. x + 3y + 2 = 0

Câu 12: Cho đàng tròn trặn (x-3)^2 + (y-1)^2 = 10. Phương trình tiếp tuyến của (C) bên trên điểm A( 4; 4) là

A. x - 3y + 5 = 0               B. x + 3y - 4 = 0                  C. x - 3y + 16 = 0              D. x + 3y - 16 = 0

Câu 13: Cho đàng tròn trặn (x-2)^2 + (y-2)^2 = 9. Phương trình tiếp tuyến của (C) trải qua điểm A( 5; -1) là

A. x + nó - 4 = 0; x - nó - 2 = 0 .                    B. x = 5; nó = -1.

C. 2x - nó - 3 = 0; 3x + 2y - 3 = 0.               D. 3x - 2y + 1 = 0; 2x + 3y + 5 = 0

Câu 14: Cho đàng tròn trặn (C): x^2 + y^2 + 2x - 6y + 5 = 0. Phương trình tiếp tuyến của (C) tuy vậy song với đường thẳng liền mạch d: x + 2y - 15 = 0 là:

A. x + 2y = 0 và x + 2y - 10 = 0.               B. x - 2y = 0 và x - 2y + 10 = 0.

C. x + 2y - 12 = 0 và x + 2y + 22 = 0       D. x + 2y + 3 = 0 và x + 2y + 7 = 0

Câu 15: Đường tròn trặn (C) đem tâm I (-1; 3) và xúc tiếp với đường thẳng liền mạch d: 3x - 4y + 5 = 0 bên trên điểm H đem tọa chừng là:

A. (-15; -75)                    B. (15; 75)                 C. (15; -75)                 D. (-15; 75)

Câu 16: Cho đàng tròn trặn (C): x^{2} + y^2 - 6x + 2y + 5 = 0 và đàng thẳng:

d: 2x + (m - 2)y - m - 7 = 0. Với độ quý hiếm nào là của m thì d là tiếp tuyến của (C)?

A. m = 3                    B. m = 15                      C. m = 13                      D. m = 3 hoặc m = 13.

Câu 17: Cho đàng tròn trặn (C) đem tâm I(-1; 2), nửa đường kính R = 29. Lập phương trình tiếp tuyến của đàng tròn trặn bên trên điểm M biết điểm M nằm trong đường thẳng liền mạch d: Viết phương trình tiếp tuyến của đàng tròn trặn câu 17 và tọa chừng M nguyên?

A. x + 2y + 3 = 0                               B. 2x + 5y + 21 = 0

C. 3x + 5y - 8 = 0                             D. Đáp án khác

Câu 18: Cho đàng tròn trặn (C): (x-3)^2+(y+3)^2=1. Qua điểm M(4;-3) hoàn toàn có thể kẻ được từng nào đường thẳng liền mạch xúc tiếp với đàng tròn trặn (C) ?

A. 0.                            B. 1.                             C. 2.                           D. Vô số.

Câu 19: Có từng nào đường thẳng liền mạch trải qua điểm N(-2; 0) xúc tiếp với đàng tròn trặn (C): (x-2)^2 + (y+3)^2 = 4?

A. 0.                           B. 1.                              C. 2.                          D. Vô số.

Câu 20: Cho đàng tròn trặn (x-3)^2 + (y+1)^2=5. Phương trình tiếp tuyến của đàng tròn (C) tuy vậy song với đường thẳng liền mạch d : 2x + nó + 7 = 0 là

A. 2x + nó = 0; 2x + nó - 10 = 0                       B. 2x + nó + 1 = 0 ; 2x + nó - 1 = 0

C. 2x - nó + 1 = 0; 2x + nó - 10 = 0                  D. 2x + nó = 0; x + 2y - 10 = 0

Đáp án khêu ý:

1 2 3 4 5 6 7 8 9 10
D D D C B A B C D D
11 12 13 14 15 16 17 18 19 20
D D B A B D B B C A

PAS VUIHOC – GIẢI PHÁP ÔN LUYỆN CÁ NHÂN HÓA

Khóa học tập online ĐẦU TIÊN VÀ DUY NHẤT:  

⭐ Xây dựng quãng thời gian học tập kể từ rơi rụng gốc cho tới 27+  

⭐ Chọn thầy cô, lớp, môn học tập theo đuổi sở thích  

⭐ Tương tác thẳng hai phía nằm trong thầy cô  

⭐ Học tới trường lại cho tới lúc nào hiểu bài xích thì thôi

⭐ Rèn tips tricks canh ty tăng cường thời hạn thực hiện đề

⭐ Tặng full cỗ tư liệu độc quyền nhập quy trình học tập tập

Xem thêm: Những bí quyết lớn chu vi hình tròn để tối ưu không gian

Đăng ký học tập demo free ngay!!

Bài ghi chép đang được tổ hợp toàn cỗ lý thuyết và cách thức ghi chép phương trình tiếp tuyến của đường tròn nhập lịch trình Toán 10. Hy vọng rằng sau nội dung bài viết này, những em học viên tiếp tục thoải mái tự tin băng qua những dạng bài xích luyện tương quan cho tới kiến thức và kỹ năng về phương trình tiếp tuyến. Để học tập nhiều hơn thế nữa những kiến thức và kỹ năng Toán 10 thú vị, những em truy vấn beyeu.edu.vn hoặc ĐK khoá học với những thầy cô VUIHOC tức thì thời điểm hôm nay nhé!

BÀI VIẾT NỔI BẬT

a) Viết công thức phân tử và công thức cấu tạo của axit axetic.b) Hoàn thành các phương trình hóa học sauCH≡CH +  ? ⟶ Br -CH=CH-BrnCH2=CH2 $\xrightarrow{{{t^0},xt,p}}$CH4 + O2 $\xrightarrow{{{t^0}}}$  ?   + H2OC2H2 +  ? $\xrightarrow{{Pd/PbC{O 3}}}$ C2H4

a) Viết công thức phân tử và công thức cấu tạo của axit axetic.b) Hoàn thành các phương trình hóa học sauCH≡CH +  ? ⟶ Br -CH=CH-BrnCH2=CH2 $\xrightarrow{{{t^0},xt,p}}$CH4 + O2 $\xrightarrow{{{t^0}}}$  ?   + H2OC2H2 +  ? $\xrightarrow{{Pd/PbC{O_3}}}$ C2H4

Những hình nền xe độ đẹp mắt nhất

Chủ đề hình nền xe độ Hình nền xe độ là sự lựa chọn hoàn hảo để làm hình nền cho máy tính và điện thoại dành cho những người yêu thích độ xe. Với những bức hình độ xe đẹp, chúng mang lại cảm giác mạnh mẽ và phong cách của những chiếc xe độ. Từ những chiếc Exciter, Satria đến Dream, những hình nền xe độ đẹp sẽ làm người dùng thỏa mãn sự đam mê và sự lạc quan khi nhìn vào những tác phẩm nghệ thuật độ xe độc đáo này.

SÊN RECTO ĐEN 428 - 108 MẮT 9 LY

Đại lý vỏ xe Phúc Thảo chuyên cung cấp các loại vỏ không ruột, vỏ có ruột và ruột xe gắn máy cho tất cả các dòng xe Honda, Yamaha, Suzuki, SYM…trên thị trường hiện nay.