Công thức tính Diện tích hình vuông, hình chữ nhật, hình tròn, hình tam giác...

Toán Tiểu học: Công thức tính diện tích S, chu vi, thể tích hình cơ phiên bản canh ty những em học viên lớp 4, 5, hệ thống hóa kiến thức và kỹ năng về tính chất diện tích S, tính chu vi, thể tích hình tam giác, hình tứ giác, hình vuông vắn, hình chữ nhật, hình trụ, hình bình hành, hình thoi, hình nón, hình cầu, hình trụ, hình lập phương, hình thang, hình vỏ hộp chữ nhật.

Qua cơ, những em đơn giản dễ dàng vận dụng vào cụ thể từng bài bác tập dượt ví dụ, nhưng mà ko bắt gặp ngẫu nhiên trở quan ngại này, nhằm càng ngày càng học tập đảm bảo chất lượng phần Hình học tập. Mời những em nằm trong theo gót dõi nội dung bài viết sau đây của Download.vn nhằm nắm rõ những công thức hình học tập cơ phiên bản nhé:

Bạn đang xem: Công thức tính Diện tích hình vuông, hình chữ nhật, hình tròn, hình tam giác...

1. Tính chu vi, diện tích S Hình chữ nhật
- Công thức tính chu vi Hình chữ nhật
- Công thức tính diện tích S Hình chữ nhật
2. Tính chu vi, diện tích S Hình vuông
- Công thức tính chu vi Hình vuông
- Công thức tính diện tích S Hình vuông
3. Tính chu vi, diện tích S Hình bình hành
- Công thức tính chu vi Hình bình hành
- Công thức tính diện tích S Hình bình hành
4. Tính chu vi, diện tích S Hình thoi
- Công thức tính chu vi Hình thoi
- Công thức tính diện tích S Hình thoi
5. Tính chu vi, diện tích S Hình tam giác
- Công thức tính chu vi Hình tam giác
- Công thức tính diện tích S Hình tam giác
6. Tính chu vi, diện tích S Hình tứ giác
- Công thức tính chu vi Hình tứ giác
- Công thức tính diện tích S Hình tứ giác
7. Tính chu vi, diện tích S Hình thang vuông, cân
- Công thức tính chu vi hình thang
- Công thức tính diện tích S hình thang
8. Tính chu vi, diện tích S hình tròn
- Công thức tính chu vi hình tròn
- Công thức tính diện tích S hình tròn
9. Tính diện tích S, thể tích hình lập phương
- Tính diện tích S xung xung quanh hình lập phương
- Tính diện tích S toàn phần hình lập phương
- Tính thể tích hình lập phương
10. Tính diện tích S, thể tích hình vỏ hộp chữ nhật
- Tính diện tích S xung xung quanh hình vỏ hộp chữ nhật
- Tính diện tích S toàn phần hình vỏ hộp chữ nhật
- Tính thể tích hình vỏ hộp chữ nhật
11. Tính diện tích S, thể tích hình nón
- Công thức tính diện tích S xung xung quanh hình nón
- Công thức tính diện tích S toàn phần hình nón
- Công thức tính thể tích hình nón
12. Tính diện tích S, thể tích hình trụ
- Công thức tính diện tích S xung xung quanh hình trụ
- Công thức tính diện tích S toàn phần hình trụ
- Công thức tính thể tích hình trụ
13. Tính chu vi, diện tích S Hình cầu
- Công thức tính diện tích S mặt mày cầu
- Công thức tính thể tích hình cầu

1. Tính chu vi, diện tích S Hình chữ nhật

Hình chữ nhật

Công thức tính chu vi Hình chữ nhật

Công thức: Phường = (a + b) x 2.

Muốn tính chu vi hình chữ nhật, tớ lấy chiều lâu năm nằm trong chiều rộng lớn nhân với 2 (cùng một đơn vị chức năng đo).

Mở rộng: thạo chu vi tính cạnh bằng phương pháp lấy nửa chu vi (P : 2) trừ cạnh tiếp tục biết.

Công thức tính diện tích S Hình chữ nhật

Công thức: S = a x b.

Muốn tính diện tích S hình chữ nhật, tớ lấy chiều lâu năm nhân với chiều rộng lớn (cùng một đơn vị chức năng đo).

Mở rộng: thạo DT dò xét cạnh bằng phương pháp lấy DT phân tách cạnh tiếp tục biết.

2. Tính chu vi, diện tích S Hình vuông

Hình vuông

Công thức tính chu vi Hình vuông

Công thức: P = a x 4

Muốn tính chu vi hình vuông vắn, tớ lấy phỏng lâu năm một cạnh nhân với 4.

Mở rộng: Nếu biết chu vi hình vuông vắn, nhằm dò xét cạnh hình vuông vắn tớ lấy chu vi hình vuông vắn phân tách 4.

Công thức tính diện tích S Hình vuông

Công thức: S = a x a.

Muốn tính diện tích S hình vuông vắn, tớ lấy phỏng lâu năm một cạnh nhân với chủ yếu nó.

Mở rộng: Nếu biết diện tích S hình vuông vắn, tớ rất có thể dò xét cạnh hình vuông vắn bằng phương pháp nhẩm.

3. Tính chu vi, diện tích S Hình bình hành

Hình bình hành

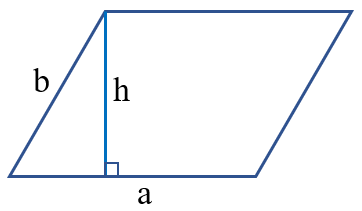
Công thức tính chu vi Hình bình hành

Công thức: P = (a + b) x 2

Muốn tính chu vi hình bình hành, tớ lấy tổng nhì cạnh kề nhân với 2 (cùng một đơn vị chức năng đo).

Mở rộng: thạo chu vi tính cạnh bằng phương pháp lấy nửa chu vi (P : 2) trừ cạnh tiếp tục biết.

Công thức tính diện tích S Hình bình hành

Công thức: S = a x h

Muốn tính diện tích S hình bình hành, tớ lấy phỏng lâu năm lòng nhân với độ cao (cùng một đơn vị chức năng đo).

Mở rộng: thạo diện tích S hình bình hành, tớ rất có thể tính:

Độ lâu năm đáy: a = S : h
Chiều cao: h = S : a

4. Tính chu vi, diện tích S Hình thoi

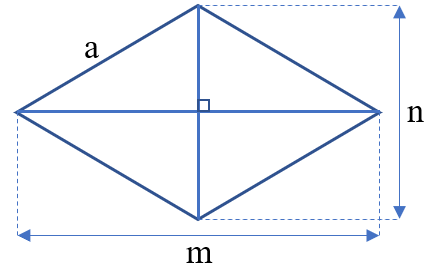
Hình thoi

Công thức tính chu vi Hình thoi

Công thức: P = a x 4

Muốn tính chu vi hình thoi, tớ lấy phỏng lâu năm cạnh hình thoi nhân với 4.

Mở rộng: Nếu biết chu vi hình thoi, nhằm dò xét cạnh hình thoi tớ lấy chu vi phân tách 4.

Công thức tính diện tích S Hình thoi

Công thức: S = $\frac{m\ \times\ n}{2}$

Muốn tính diện tích S hình thoi, tớ lấy tích phỏng lâu năm hai tuyến đường chéo cánh phân tách mang đến 2 (cùng một đơn vị chức năng đo).

5. Tính chu vi, diện tích S Hình tam giác

Hình tam giác

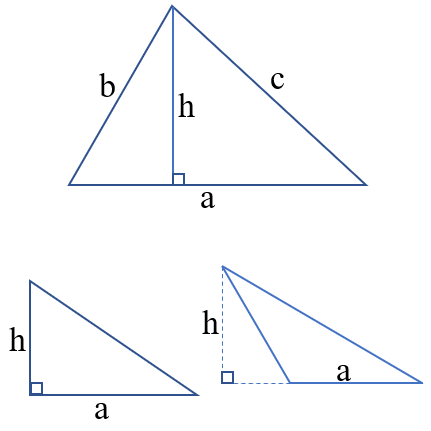
Công thức tính chu vi Hình tam giác

Công thức: C = a + b + c

Muốn tính chu vi hình tam giác, tớ lấy phỏng lâu năm 3 cạnh tam giác nằm trong lại cùng nhau (cùng một đơn vị chức năng đo).

Mở rộng: Nếu biết chu vi hình tam giác và 2 cạnh, tớ dò xét cạnh còn sót lại bằng phương pháp lấy chu vi trừ lên đường tổng 2 cạnh còn lại: a = C - (b+c).

Công thức tính diện tích S Hình tam giác

Công thức: S = $\frac{a\ \times\ h}{2}$

Muốn tính diện tích S hình tam giác, tớ lấy phỏng lâu năm lòng nhân với độ cao rồi phân tách mang đến 2 (cùng một đơn vị chức năng đo).

Mở rộng: Nếu tớ biết diện tích S hình tam giác, tớ rất có thể tính:

Chiều cao: h = (S x 2) : a
Cạnh đáy: a = (S x 2) : h

6. Tính chu vi, diện tích S Hình tứ giác

Hình tứ giác

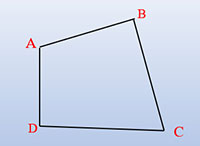
Công thức tính chu vi Hình tứ giác

Công thức: Phường = a + b + c + d

Trong đó:

P là chu vi hình tứ giác
a, b, c, d theo lần lượt là phỏng lâu năm những cạnh của tứ giác

Công thức tính diện tích S Hình tứ giác

Sẽ không tồn tại công thức công cộng nhằm tính diện tích S hình tứ giác nhưng mà tất cả chúng ta phụ thuộc ví dụ hình tứ giác này là gì để sở hữu cách tính diện tích không giống nhau.

7. Tính chu vi, diện tích S Hình thang vuông, cân

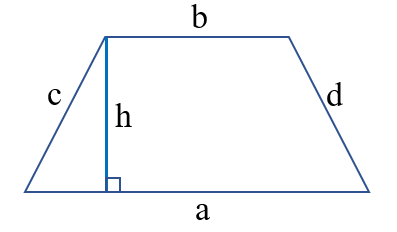
Hình thang

Có một cạnh mặt mày vuông góc với nhì lòng, cạnh vị trí kia đó là độ cao hình thang vuông. Khi tính diện tích S hình thang vuông tớ tính như cơ hội dò xét hình thang.

Hình thang cân: với hai tuyến đường chéo cánh đều nhau, nhì góc tù đều nhau và nhì góc nhọn đều nhau.

Xem thêm: Công thức làm sữa hạt bằng máy cực nhanh

Công thức tính chu vi hình thang

Công thức: C = a + b + c + d

Muốn tính chu vi hình thang, tớ lấy phỏng lâu năm những cạnh hình thang nằm trong lại cùng nhau (cùng một đơn vị chức năng đo).

Mở rộng: Nếu biết chu vi hình thang và phỏng lâu năm 3 cạnh, tớ rất có thể dò xét cạnh còn sót lại bằng phương pháp lấy chu vi trừ lên đường tổng phỏng lâu năm 3 cạnh: a = C - (b + c + d).

Công thức tính diện tích S hình thang

Công thức: S = $\frac{\left(a\ +\ b\right)\ \times\ h}{2}$

Muốn tính diện tích S hình thang, tớ lấy tổng phỏng lâu năm nhì lòng nhân với độ cao rồi rước phân tách mang đến 2 (cùng một đơn vị chức năng đo).

Mở rộng: Nếu biết diện tích S hình thang, tớ rất có thể tính

Chiều cao: h = (S x 2) : a
Cạnh đáy: a = (S x 2) : h

8. Tính chu vi, diện tích S hình tròn

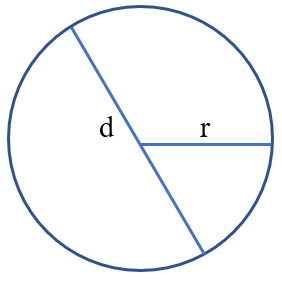
Hình tròn

Công thức tính chu vi hình tròn

Công thức: C = d x 3,14
hoặc r x 2 x 3,14

Muốn tính chu vi hình trụ, tớ lấy 2 lần bán kính nhân với số 3,14 (hoặc lấy nửa đường kính nhân 2 rồi nhân với 3,14).

Mở rộng: Nếu biết chu vi hình trụ, tớ rất có thể tính:

Đường kính: d = C : 3,14
Bán kính: r = C : 3,14 : 2

Công thức tính diện tích S hình tròn

Công thức: r x r x 3,14

Muốn tính diện tích S hình trụ, tớ lấy buôn bán kinh nhân với nửa đường kính rồi nhân với số 3,14.

9. Tính diện tích S, thể tích hình lập phương

Hình lập phương

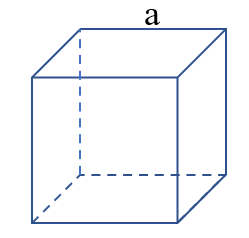
Tính diện tích S xung xung quanh hình lập phương

Công thức: S_xq = S_m x 4

Muốn tính diện tích S xung xung quanh, tớ lấy diện tích S một mặt của hình lập phương nhân với 4.

Tính diện tích S toàn phần hình lập phương

Công thức: S_tp = S_m x 6

Muốn tính diện tích S xung xung quanh, tớ lấy diện tích S một mặt của hình lập phương nhân với 6.

Tính thể tích hình lập phương

Công thức: V = a x a x a

Muốn tính thể tích hình lập phương, tớ lấy cạnh nhân với cạnh rồi nhân với cạnh.

10. Tính diện tích S, thể tích hình vỏ hộp chữ nhật

Hình vỏ hộp chữ nhật

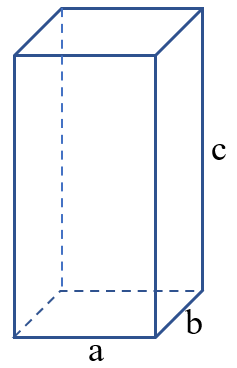
Tính diện tích S xung xung quanh hình vỏ hộp chữ nhật

Công thức: S_xq = Phường x c

Muốn tính diện tích S xung xung quanh của hình vỏ hộp chữ nhật, tớ lấy chu vi mặt mày lòng nhân với độ cao (cùng một đơn vị chức năng đo).

Tính diện tích S toàn phần hình vỏ hộp chữ nhật

Công thức: S_tp = S_xq + S_đ x 2

Muốn tính diện tích S toàn phần của hình vỏ hộp chữ nhật, tớ lấy diện tích S xung xung quanh của hình vỏ hộp chữ nhật cùng theo với gấp đôi diện tích S lòng (cùng một đơn vị chức năng đo).

Tính thể tích hình vỏ hộp chữ nhật

Công thức: V = a x b x c

Muốn tính thể tích của hình vỏ hộp chữ nhật, tớ lấy chiều rài nhân với chiều rộng lớn rồi nhân với độ cao (cùng một đơn vị chức năng đo).

11. Tính diện tích S, thể tích hình nón

Công thức tính diện tích S xung xung quanh hình nón

Diện tích xung xung quanh hình nón được xác lập vì như thế tích của hằng số Pi (π) nhân với nửa đường kính lòng hình nón (r) nhân với đàng sinh hình nón (l). Đường sinh rất có thể là một trong đường thẳng liền mạch hoặc 1 đàng cong phẳng lì. Với hình nón thì đàng sinh với chiều lâu năm kể từ mép của vòng tròn trĩnh cho tới đỉnh của hình nón.

$Sxq=\pi.r.l$

Trong đó:

Sxq: là ký hiệu diện tích S xung xung quanh hình nón.
π: là hằng số Pi có mức giá trị xấp xỉ là 3,14
r: Bán kính mặt mày lòng hình nón và vì như thế 2 lần bán kính phân tách 2 (r = d/2).
l: đàng sinh của hình nón.

Công thức tính diện tích S toàn phần hình nón

Diện tích toàn phần hình nón vì như thế diện tích S xung xung quanh hình nón cùng theo với diện tích S mặt mày lòng hình nón. Vì diện tích S mặt mày lòng là hình trụ nên vận dụng công thức tính diện tích S hình trụ là Sđ = π.r.r.

$Stp=Sxq+Sd=\pi.r.l+\pi.r^2$