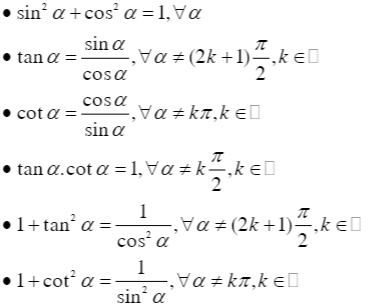Giới hạn hàm lượng giác : Những điều thú vị bạn chưa biết

Để tính số lượng giới hạn của hàm con số giác, tất cả chúng ta cần thiết nắm rõ một trong những công thức lượng giác cơ bạn dạng như sin, cos, và tan. Dưới đó là một trong những bước triển khai nhằm tính số lượng giới hạn của hàm con số giác:
Bước 1: Xác lăm le điểm số lượng giới hạn. Điểm số lượng giới hạn thông thường là một trong những độ quý hiếm xác lập nhập miền số lượng giới hạn của hàm số. Ví dụ: số lượng giới hạn của hàm số sin(x) Khi x tiến bộ cho tới 0.
Bước 2: kề dụng công thức lượng giác. Sử dụng những công thức lượng giác nhằm tính độ quý hiếm của hàm con số giác bên trên điểm số lượng giới hạn. Ví dụ: nếu như số lượng giới hạn của hàm số là sin(x) Khi x tiến bộ cho tới 0, tao hoàn toàn có thể dùng công thức lượng giác cơ bạn dạng sin(0) = 0 nhằm tính độ quý hiếm số lượng giới hạn.
Bước 3: Ràng buộc miền số lượng giới hạn. Kiểm tra coi hàm số với buộc ràng miền số lượng giới hạn ko. Ví dụ: hàm số tan(x) với miền số lượng giới hạn kể từ -π/2 cho tới π/2. Do cơ, nếu như tao tính số lượng giới hạn của hàm số tan(x) Khi x tiến bộ cho tới π/2, số lượng giới hạn này sẽ không còn xác lập.
Bước 4: Lặp lại tiến độ cho những số lượng giới hạn không giống nhau. Nếu có rất nhiều điểm số lượng giới hạn nhập miền số lượng giới hạn của hàm số, tao cần thiết tái diễn công việc bên trên nhằm tính số lượng giới hạn bên trên từng điểm.
Chúng tao cũng hoàn toàn có thể tận dụng tối đa những công thức lượng giác phức tạp hơn hoàn toàn như là lăm le lí L\'Hôpital nhằm tính số lượng giới hạn của những hàm con số giác phức tạp rộng lớn. Tuy nhiên, tiến độ cơ bạn dạng bên trên hoàn toàn có thể được vận dụng cho tới đa số những tình huống.

Bạn đang xem: Giới hạn hàm lượng giác : Những điều thú vị bạn chưa biết

Giới hạn nhập nồng độ giác là độ quý hiếm tuy nhiên hàm số tiến bộ cho tới Khi đổi mới số song lập tiến bộ cho tới một độ quý hiếm chắc chắn. Để tính số lượng giới hạn của hàm con số giác, tất cả chúng ta cần thiết nắm rõ những công thức lượng giác cơ bạn dạng như sin, cos, tan, cùng theo với những đặc thù của bọn chúng. Cần phân biệt số lượng giới hạn của hàm số trong những tình huống bên trên những số lượng giới hạn tiến bộ về âm vô nằm trong, dương vô nằm trong và những số lượng giới hạn tiến bộ về những độ quý hiếm quan trọng như 0, π/2, -π/2. Sau cơ, tất cả chúng ta vận dụng những quy tắc tính số lượng giới hạn nhằm đo lường độ quý hiếm sau cuối.

Để tính được số lượng giới hạn của hàm con số giác, tao cần thiết thực hiện như sau:
Bước 1: Xác lăm le coi hàm số cần thiết tính số lượng giới hạn là hàm con số giác nào là (sin, cos, tan, cot, csc, sec).
Bước 2: Xác định vị trị x tuy nhiên số lượng giới hạn của hàm số rất cần được tính bên trên cơ. Giá trị x này hoàn toàn có thể là một trong những rõ ràng hoặc là vô nằm trong (±∞).
Bước 3: kề dụng công thức lượng giác ứng nhằm tính độ quý hiếm của hàm số bên trên độ quý hiếm x một vừa hai phải xác lập.
Bước 4: Kiểm tra coi độ quý hiếm của hàm số bên trên x với quy tụ về một độ quý hiếm xác lập Khi x tiến bộ cho tới số lượng giới hạn đang rất được xét hay là không. Nếu với, thành phẩm là độ quý hiếm quy tụ này; còn nếu không, số lượng giới hạn ko tồn bên trên.
Bước 5: Nếu số lượng giới hạn tồn bên trên, thành phẩm là độ quý hiếm quy tụ của hàm số bên trên x.
Ví dụ: Để tính số lượng giới hạn của hàm số sin(x) Khi x tiến bộ cho tới 0:
Bước 1: Hàm số cần thiết tính số lượng giới hạn là hàm sin(x).
Bước 2: Giá trị x cần thiết tính số lượng giới hạn là 0.
Bước 3: kề dụng công thức lượng giác, tao với sin(0) = 0.
Bước 4: Kiểm tra hàm số với quy tụ về một độ quý hiếm xác lập Khi x tiến bộ cho tới 0 bằng phương pháp tính độ quý hiếm của hàm số bên trên những điểm x tiến bộ cho tới 0 kể từ những phía không giống nhau. Kết trái khoáy là hàm số quy tụ về 0 Khi x tiến bộ cho tới 0.
Bước 5: Giới hạn của hàm số sin(x) Khi x tiến bộ cho tới 0 là 0.
Chú ý: Việc tính số lượng giới hạn của hàm con số giác hoàn toàn có thể phức tạp rộng lớn và yên cầu sự nắm rõ những công thức lượng giác và kĩ năng vận dụng đúng chuẩn công thức vào cụ thể từng tình huống rõ ràng.

Công thức lượng giác thông thường được dùng nhằm tính số lượng giới hạn nhập hàm con số giác là công thức lượng giác cơ bạn dạng và những công thức lượng giác tương quan cho tới nhau. Dưới đó là một trong những công thức lượng giác thông thường được sử dụng:
1. Công thức lượng giác cơ bản:
- sin(x) / x → 1, Khi x tiến bộ cho tới 0
- cos(x) / x → 1, Khi x tiến bộ cho tới 0
- tan(x) / x → 1, Khi x tiến bộ cho tới 0
2. Công thức tương quan cho tới hàm số sin(x):
- (1 - cos(x)) / x → 0, Khi x tiến bộ cho tới 0
- (sin(x + y) - sin(x)) / nó → cos(x), Khi nó tiến bộ cho tới 0
3. Công thức tương quan cho tới hàm số cos(x):
- (1 - cos(x)) / x → 0, Khi x tiến bộ cho tới 0
- (cos(x + y) - cos(x)) / nó → -sin(x), Khi nó tiến bộ cho tới 0
Ngoài rời khỏi, còn tồn tại những công thức lượng giác không giống nếu như tất cả chúng ta mong muốn tính số lượng giới hạn của những hàm con số giác phức tạp rộng lớn. Tuy nhiên, công thức lượng giác cơ bạn dạng và những công thức tương quan bên trên là những công thức cần thiết và thông thường được dùng trong những việc tính số lượng giới hạn của hàm con số giác.

Chúng tao cần dùng lăm le lí 1 nhằm tính số lượng giới hạn của hàm con số giác Khi hàm số đang rất được đều quy tụ và số lượng giới hạn của chính nó hoàn toàn có thể dễ dàng và đơn giản được xem toán. Định lí 1 của số lượng giới hạn hàm con số giác là: Giới hạn của hàm số sin(x)/x Khi x tiến bộ cho tới 0 là một trong những. Tuy nhiên, nhằm vận dụng lăm le lí này, tao cần chắc hẳn rằng rằng hàm số sin(x)/x đang rất được đều quy tụ và số lượng giới hạn của chính nó hoàn toàn có thể được xem toán.

Quy tắc l\'Hôpital ko được vận dụng Khi tính số lượng giới hạn hàm con số giác vì như thế quy tắc này chỉ vận dụng cho những hàm số tuần trả, tức là hàm số ngay gần cho tới số lượng giới hạn hoàn toàn có thể được màn trình diễn bên dưới dạng tổ hợp của hàm số không giống. Tuy nhiên, nhập tình huống số lượng giới hạn của hàm con số giác, hàm số ko tuần trả và ko thể màn trình diễn bên dưới dạng tổ hợp của hàm số không giống. Do cơ, quy tắc l\'Hôpital ko vận dụng được. Để tính số lượng giới hạn của hàm con số giác, tất cả chúng ta cần dùng những công thức tương quan cho tới lượng giác và những quy tắc khác ví như lăm le lí 1 nhằm giải quyết và xử lý.

0.
Để tính số lượng giới hạn của hàm số \\(\\frac{{\\sin x}}{x}\\) Khi \\(x\\) dần dần tiến bộ cho tới 0, tao hoàn toàn có thể dùng công thức số lượng giới hạn căn bạn dạng sau:
\\[\\lim_{x \\to a} \\frac{{\\sin x}}{x} = 1\\]
Tuy nhiên, công thức này chỉ vận dụng Khi \\(a\\) là một trong những thực và \\(\\sin a\\) không giống 0. Trong tình huống này, Khi \\(x \\to 0\\), tao thấy \\(\\sin x\\) cũng tiếp tục tiến bộ dần dần cho tới 0. Tuy nhiên, tao ko thể vận dụng thẳng công thức số lượng giới hạn căn bạn dạng vì như thế kiểu mẫu số của tất cả chúng ta là \\(x\\) và \\(x\\) tiến bộ dần dần cho tới 0.
Để giải quyết và xử lý yếu tố này, tao hoàn toàn có thể dùng một trong những quy tắc thay đổi nhằm quy đổi vấn đề về một dạng hoàn toàn có thể tính được. Ta tiếp tục xét hàm số \\(f(x) = \\frac{{\\sin x}}{x}\\).
Đầu tiên, tao hoàn toàn có thể dùng công thức goniômetri \\(\\sin x = x - \\frac{{x^3}}{3!} + \\frac{{x^5}}{5!} - \\frac{{x^7}}{7!} + \\ldots\\), được gọi là chuỗi Maclaurin của \\(\\sin x\\), nhằm không ngừng mở rộng \\(\\sin x\\) trở nên một chuỗi của \\(x\\) Khi \\(x\\) tiến bộ dần dần cho tới 0.
\\[f(x) = \\frac{{\\sin x}}{x} = \\frac{{x - \\frac{{x^3}}{3!} + \\frac{{x^5}}{5!} - \\frac{{x^7}}{7!} + \\ldots}}{x} = 1 - \\frac{{x^2}}{3!} + \\frac{{x^4}}{5!} - \\frac{{x^6}}{7!} + \\ldots\\]
Tiếp theo đuổi, tao tiếp tục vô hiệu hóa một trong những bộ phận ko tác động cho tới số lượng giới hạn Khi \\(x\\) tiến bộ dần dần cho tới 0. Theo công thức bên trên, những bộ phận chứa chấp \\(x\\) nón lẻ Khi \\(x\\) tiến bộ dần dần cho tới 0 đều vị 0. Vì vậy, tao chỉ quan hoài cho tới những bộ phận chứa chấp \\(x\\) nón chẵn.
\\[f(x) = 1 - \\frac{{x^2}}{3!} + \\frac{{x^4}}{5!} - \\frac{{x^6}}{7!} + \\ldots\\]
Tiếp theo đuổi, tao để ý thấy rằng nhập chuỗi bên trên, từng bộ phận tiếp sau với index của \\(x\\) nón to hơn cút 2 và vị \\((-1)^{n+1} \\cdot \\frac{{x^{2n}}}{(2n + 1)!}\\), với \\(n\\) là số đương nhiên.
Dựa bên trên để ý này, tao hoàn toàn có thể màn trình diễn \\(f(x)\\) bên dưới dạng một chuỗi vô hạn như sau:
\\[f(x) = 1 - \\frac{{x^2}}{3!} + \\frac{{x^4}}{5!} - \\frac{{x^6}}{7!} + \\ldots = \\sum_{n=0}^{\\infty} (-1)^{n} \\cdot \\frac{{x^{2n}}}{(2n + 1)!}\\]
Cuối nằm trong, tao dùng định nghĩa về số lượng giới hạn của chuỗi vô hạn nhằm tính số lượng giới hạn của \\(f(x)\\) Khi \\(x\\) tiến bộ dần dần cho tới 0:
\\[\\lim_{x \\to 0} f(x) = \\lim_{x \\to 0} \\sum_{n=0}^{\\infty} (-1)^{n} \\cdot \\frac{{x^{2n}}}{(2n + 1)!} = 1\\]
Vậy, số lượng giới hạn của \\(\\frac{{\\sin x}}{x}\\) Khi \\(x\\) dần dần tiến bộ cho tới 0 là một trong những.

vô nằm trong.
Để tính số lượng giới hạn của hàm con số giác tanx/x Khi x tiến bộ cho tới vô nằm trong, tất cả chúng ta hoàn toàn có thể vận dụng quy tắc l\'Hôpital. Theo quy tắc này, nếu như một hàm số được màn trình diễn bên dưới dạng một quy tắc phân chia thân ái nhì hàm số và Khi đo lường số lượng giới hạn của chính nó bắt gặp cần dạng ko xác lập như 0/0 hoặc vô cùng/vô nằm trong, tao hoàn toàn có thể lấy đạo hàm của hàm số nhập tử số và kiểu mẫu số, tiếp sau đó tính số lượng giới hạn của nhì hàm số này.
Áp dụng quy tắc l\'Hôpital:
* Tính đạo hàm của tử số và kiểu mẫu số:
Tính đạo hàm của tanx, tao có: d(tanx)/dx = sec^2(x)
Tính đạo hàm của x, tao có: d(x)/dx = 1
* Tính số lượng giới hạn của đạo hàm:
Giới hạn của đạo hàm của tanx Khi x tiến bộ cho tới vô nằm trong là số lượng giới hạn của sec^2(x) Khi x tiến bộ cho tới vô nằm trong.
Với hàm số sec^2(x), tao thấy Khi x tiến bộ cho tới vô nằm trong, độ quý hiếm của sec^2(x) cũng tiến bộ cho tới vô nằm trong, vì như thế sec^2(x) là hàm số bị ngăn bên trên vị số lượng giới hạn 1 và âm vô nằm trong.
Do cơ, số lượng giới hạn của tanx/x Khi x tiến bộ cho tới vô nằm trong là vô nằm trong.

Với vấn đề tính số lượng giới hạn của hàm số (1-cosx)/x^2 Khi x dần dần tiến bộ cho tới 0, tao hoàn toàn có thể vận dụng công thức số lượng giới hạn của hàm con số giác.
Để tính số lượng giới hạn này, tao triển khai công việc sau:
Bước 1: Tìm hàm số giao động nhằm ước tính hàm số lúc đầu. Trong tình huống này, tao hoàn toàn có thể dùng công thức số lượng giới hạn của cosx.
Bước 2: Thực hiện tại những quy tắc thay đổi vận dụng công thức số lượng giới hạn. Trong tình huống này, tao tiếp tục tính số lượng giới hạn của (1 - cosx) / x^2 Khi x dần dần tiến bộ cho tới 0.
Áp dụng công thức số lượng giới hạn của hàm con số giác, tao có:
lim(x->0) (1 - cosx) / x^2 = lim(x->0) (1 - cosx) / (x^2.sin^2(x) / sin^2(x)) = lim(x->0) [sin^2(x) / x^2] * [(1 - cosx) / sin^2(x)]
= lim(x->0) [sinx / x]^2 * [(1 - cosx) / sin^2(x)]
Với số lượng giới hạn lim(x->0) [sinx / x] = 1 và lim(x->0) (1 - cosx) = 0, tao có:
lim(x->0) (1 - cosx) / x^2 = 1 * 0 = 0.
Vậy, số lượng giới hạn của hàm số (1-cosx)/x^2 Khi x dần dần tiến bộ cho tới 0 là 0.

Xem thêm: Các giải bài toán bằng cách lập phương trình lớp 9 (cực hay, có đáp án).

Để tính số lượng giới hạn của hàm số (1+sinx)/cosx Khi x dần dần tiến bộ cho tới 0, tao hoàn toàn có thể vận dụng những công thức lượng giác nhằm đơn giản và giản dị hóa biểu thức này.
Đầu tiên, tao thấy rằng nhập số lượng giới hạn này, Khi x tiến bộ cho tới 0, công thức (1+sinx)/cosx tiếp tục phân chia cho tới 0. Tuy nhiên, tao hiểu được cosx ko khi nào vị 0 Khi x là số thực.
Vì vậy, tao hoàn toàn có thể dùng Quy tắc Lôpital nhằm tính số lượng giới hạn của biểu thức này. Quy tắc Lôpital được cho phép tao tính số lượng giới hạn của một hàm số Khi biểu thức gốc phân chia cho tới 0 hoặc với dạng vô hạn.
Áp dụng Quy tắc Lôpital, tao triển khai công việc sau:
1. Đặt hàm số lúc đầu là f(x) = (1+sinx)/cosx.
2. Tính đạo hàm của f(x) theo đuổi x.
3. Gọi hàm số mới nhất là g(x) và tính số lượng giới hạn của g(x) Khi x tiến bộ cho tới 0.
Tiếp theo đuổi, tao tiếp tục triển khai công việc trên:
1. Đặt f(x) = (1+sinx)/cosx.
2. Tính đạo hàm của f(x) theo đuổi x:
f\'(x) = [(cosx)(cosx) - (1+sinx)(-sinx)] / (cosx)^2
= (cos^2x + sin^2x - sinx + sin^2x) / (cosx)^2
= (2sin^2x - sinx + 1) / (cosx)^2
3. Đặt g(x) = (2sin^2x - sinx + 1) / (cosx)^2.
Tính số lượng giới hạn của g(x) Khi x tiến bộ cho tới 0:
lim[x->0] g(x) = lim[x->0] [(2sin^2x - sinx + 1) / (cosx)^2]
= [(2sin^20 - sin0 + 1) / (cos0)^2]
= [0 + 1] / 1
= 1.
Ý nghĩa của thành phẩm này là số lượng giới hạn của hàm số (1+sinx)/cosx Khi x tiến bộ cho tới 0 là một trong những.