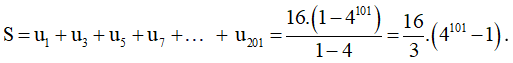Bài viết lách Các công thức về cấp số nhân không thiếu nhất Toán lớp 11 hoặc nhất bao gồm 4 phần: Định nghĩa, Công thức, Kiến thức không ngừng mở rộng và Bài luyện minh họa vận dụng công thức nhập bài bác đem tiếng giải cụ thể hùn học viên dễ dàng học tập, dễ dàng lưu giữ Các công thức về cấp số nhân không thiếu nhất.
Cấp số nhân là gì? Công thức cấp số nhân cụ thể, dễ dàng hiểu
Bạn đang xem: Cấp số nhân là gì? Công thức cấp số nhân chi tiết, dễ hiểu
1. Lý thuyết
a) Định nghĩa:
Cấp số nhân là một trong sản phẩm số (hữu hạn hoặc vô hạn), nhập cơ Tính từ lúc số hạng loại nhị, từng số hạng đều là tích của số hạng đứng ngay lập tức trước nó với một số trong những ko thay đổi q.
Số q được gọi là công bội của cấp số nhân.
Nếu (un) là cấp số nhân với công bội q, tớ đem công thức truy hồi: un = un-1 . q với n ∈ N*
Đặc biệt:
- Khi q = 0, cấp số nhân đem dạng u1; 0; 0; … 0; …
- Khi q = 1, cấp số nhân đem dạng u1; u1; … u1;…
- Khi u1 = 0 thì với từng q, cấp số nhân đem dạng 0; 0; 0; … 0; …
b) Số hạng tổng quát lác của cấp số nhân (un) được xác lập bởi vì công thức:
un = u1 . qn - 1 với ∀n ∈ N*, n ≥ 2
c) Tính chất
Ba số hạng uk - 1, uk, uk + 1 là thân phụ số hạng liên tục của cung cấp số nằm trong khi và chỉ khi uk2 = uk-1.uk+1 với k ≥ 2
d) Tổng n số hạng trước tiên của cấp số nhân được xác lập bởi vì công thức:
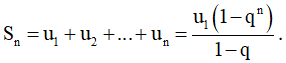
Chú ý: Nếu q = 1 thì cấp số nhân là u1; u1; u1; … u1;.. khi cơ Sn = n.u1.

2. Công thức
- Công thức truy hồi: un = un-1 . q với n ∈ N*
- Công thức số hạng tổng quát: un = u1 . qn - 1 với ∀n ∈ N, n ≥ 2
- Ba số hạng uk - 1, uk, uk + 1 là thân phụ số hạng liên tục của cung cấp số nằm trong khi và chỉ khi uk2 = uk-1.uk+1 với k ≥ 2
- Tổng n số hạng đầu tiên: 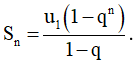
3. Ví dụ minh họa
Ví dụ 1: Cho cấp số nhân (un) với u1 = 3, q = – 2.
a) Tính số hạng loại 25 của cấp số nhân.
b) Số 49152 là số hạng loại từng nào của cấp số nhân.
c) Tính tổng của 100 số hạng trước tiên của cấp số nhân.
Lời giải
Xem thêm: Hình Nền OPPO ❤️ Tuyển Tập Ảnh Nền Điện Thoại OPPO - Gấu Đây - Takimart
a) Số hạng loại 25 của cung cấp số cộng: u25 = u1 . q25-1 = 3.(– 2)24 = 3.224.
b) Gọi số hạng loại k là số 49152, tớ có
uk = u1.qk-1 = 49152
⇔ 3.(-2)k-1 = 49152
⇔ (-2)k-1 = 16384 = (-2)14
⇔ k = 15
Vậy số 49152 là số hạng loại 15 của cấp số nhân.
c) Tổng 100 số hạng đầu tiên:
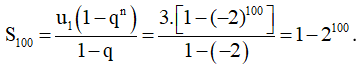
Ví dụ 2: Cho cấp số nhân (un) thỏa mãn: 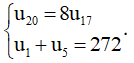
a) Tìm số hạng trước tiên và công bội của cấp số nhân.
b) Tính tổng 100 số hạng đầu tiên của cấp số nhân.
c) Tính tổng S = u1 + u3 + u5 +u7 +…+ u201.
Lời giải
a) Gọi d là công sai của cung cấp số nằm trong, tớ có:
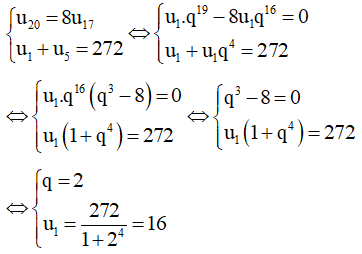
Vậy u1 = 16 và q = 2.
b) Tổng 100 số hạng đầu tiên:
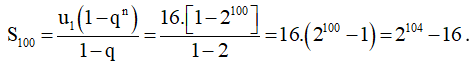
c) Dãy số là (vn): u1; u3; u5; u7; … u201 là cấp số nhân với số hạng trước tiên là u1 và công bội 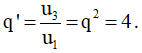
Dãy (vn) có 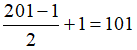 số hạng
số hạng
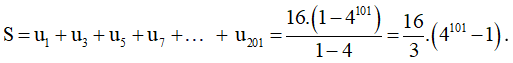
4. Giải đáp thắc mắc
4.1 Cấp số nhân là gì và cơ hội xác lập công thức tổng của nó?
Cấp số nhân là một trong sản phẩm số nhập cơ từng số tiếp sau đó đều bởi vì một hằng số gọi là công bội nhân với số trước cơ nhằm chiếm được số tiếp sau. Công thức tổng của cấp số nhân là S_n = a * (1 - r^n) / (1 - r), nhập cơ S_n là tổng n số trước tiên của cấp số nhân, n là con số số nhập sản phẩm, a là số hạng trước tiên và r là công bội.
4.2 Các đặc thù quan trọng của cấp số nhân là gì?
Cấp số nhân đem những đặc thù quan trọng như tổng n số trước tiên, tổng vô hạn và giới hạn của cấp số nhân. Khi độ quý hiếm của công bội nhân r ở trong tầm -1 cho tới 1, cấp số nhân quy tụ về một độ quý hiếm thắt chặt và cố định khi con số số nhập sản phẩm tiến bộ cho tới vô nằm trong.
Xem thêm: Những bí quyết lớn chu vi hình tròn để tối ưu không gian
4.3 Cách tính số hạng loại n nhập cấp số nhân?
Để tính số hạng loại n nhập cấp số nhân, tớ dùng công thức a_n = a * r^(n-1), nhập cơ a_n là số hạng loại n, a là số hạng trước tiên, r là công bội và n là số trật tự của số hạng cần thiết tính.
4.4 Ứng dụng của cấp số nhân nhập thực tiễn là gì?
Cấp số nhân có rất nhiều phần mềm nhập thực tiễn như nhập tài chủ yếu, tài chính, khoa học tập PC, xử lý tín hiệu, và nhiều nghành nghề không giống. Ví dụ, nhập tài chủ yếu, cấp số nhân được dùng nhằm tính lãi vay lũy tiến; nhập khoa học tập PC, nó được vận dụng trong số thuật toán tối ưu và mã hóa vấn đề.
Trên đấy là một số trong những share của doanh nghiệp Luật ACC về Cấp số nhân là gì? Công thức cấp số nhân cụ thể, dễ dàng hiểu. Nếu đem ngẫu nhiên vướng mắc hoặc yếu tố nào là tương quan cho tới yếu tố này hãy contact với ACC và để được trả lời nhé!

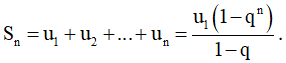

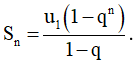
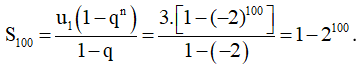
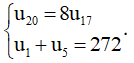
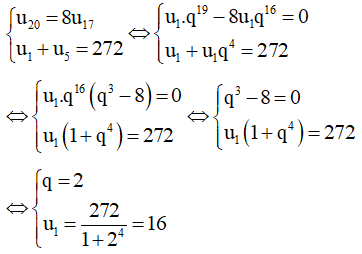
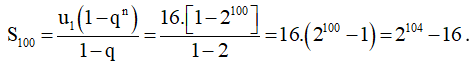
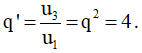
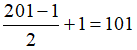 số hạng
số hạng