Công thức tính thể tích hình trụ, diện tích xung quanh và toàn phần hình trụ tròn

Cách tính thể tích hình trụ, diện tích S hình trụ

Công thức tính thể tích hình trụ, diện tích S xung xung quanh và toàn phần hình trụ tròn xoe với những ví dụ trực quan liêu mang đến chúng ta tóm được phương pháp tính thể tích, diện tích S xung xung quanh và toàn phần của hình trụ vận dụng vô những câu hỏi và phần mềm thực tiễn. Mời chúng ta nằm trong xem thêm.

• Công thức tính chu vi hình trụ và diện tích S hình tròn
• Công thức tính thể tích hình lập phương, diện tích S hình lập phương

Hình trụ là gì?

Khi tảo hình chữ nhật ABCD một vòng xung quanh cạnh CD cố định và thắt chặt tớ nhận được một hình trụ.

– Hai lòng là hình trụ đều nhau và phía trên nhị mặt mày bằng tuy nhiên tuy nhiên.

– DC là trục của hình trụ.

– Các đàng sinh của hình trụ( ví dụ điển hình EF) vuông góc với nhị mặt mày lòng.

Độ nhiều năm đàng sinh cũng chính là chừng nhiều năm đàng cao của hình trụ.

Hình trụ được dùng khá thông dụng trong những câu hỏi hình học tập kể từ căn phiên bản cho tới phức tạp, vô cơ công thức tính diện tích S, thể tích hình trụ thông thường được dùng không giống thông dụng trong những việc tính một không khí chắc chắn bị cướp lưu giữ bởi vì một hình trụ.

Bên cạnh cơ, công thức tính diện tích S, thể tích hình trụ cũng khá được vận dụng trong những dạng câu hỏi tinh vi tăng phương pháp tính thể tích hình lập phương hoặc diện tích S hình chữ nhật. Cùng xem thêm công thức tính thể tích hình trụ và những ví dụ trực quan liêu nhất vô phương pháp tính diện tích S, thể tích hình trụ.

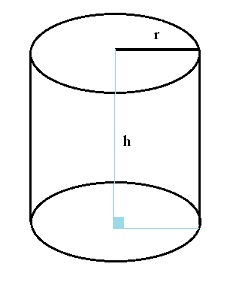
Công thức và phương pháp tính diện tích S hình trụ

Diện tích hình trụ là toàn cỗ không khí cướp lưu giữ bằng phương pháp tính tổng diện tích S xung xung quanh và diện tích S nhị lòng. Trong Lúc cơ, diện tích S toàn phần hình trụ là diện tích S của mặt mày xung xung quanh hình trụ, ko bao gồm diện tích S nhị lòng.

1. Công Thức Tính Diện Tích Xung Quanh Hình Trụ

S_{xung quanh} = 2 x π x r x h

Trong đó:

+ r: nửa đường kính hình trụ

+ h: độ cao nối kể từ lòng cho tới đỉnh hình trụ

2. Công Thức Tính Diện Tích Toàn Phần Hình Trụ

S _{toàn phần} = 2 x π x r² + 2 x π x r x h = 2 π x r x (r + h)

Trong đó:

+ r: nửa đường kính hình trụ

+ 2 x π x r x h: diện tích S xung xung quanh hình trụ

+ 2 x π x r²: diện tích S của nhị đáy

3. Ví Dụ Cách Tính Diện Tích Hình Trụ

Ví dụ 1: Cho một hình trụ sở hữu nửa đường kính đàng tròn xoe lòng là 6 centimet, trong lúc cơ độ cao nối kể từ lòng cho tới đỉnh hình trụ dày 8 centimet. Hỏi diện tích S xung xung quanh và diện tích S toàn phần của hình trụ bởi vì bao nhiêu?

Hướng dẫn:

Diện tích xung xung quanh của hình trụ: S_xq = 2 x π x r x h

Diện tích toàn phần của hình trụ: S_tp = 2 x π x r² + 2 x π x r x h = 2 π x r x (r + h)

Lời giải:

Xem thêm: Công thức tính thể tích khối chóp dễ hiểu nhất

Theo công thức tớ sở hữu cung cấp đàng tròn xoe lòng r = 6 centimet và độ cao của hình trụ h = 8 centimet. Suy đi ra tớ sở hữu công thức tính diện tích S xung xung quanh hình trụ và diện tích S toàn phần hình trụ bằng:

Diện tích xung xung quanh hình trụ = 2 x π x r x h = 2 x π x 6 x 8 = ~ 301 cm²

Diện tích toàn phần hình trụ = 2 π x r x (r + h) = 2 X π x 6 x (6 + 8) = ~ 527 cm².

Ví dụ 2: Cho hình trụ sở hữu độ cao 5cm nửa đường kính lòng bởi vì 3cm. Tính diện tích S xung xung quanh, diện tích S toàn phần của hình trụ?

Lời giải:

Diện tích xung xung quanh của hình trụ: S_xq = 2 x π x r x h = 2 x π x 3 x 5 = 30 π ~  94,25 cm²

Diện tích toàn phần của hình trụ: S_tp = 2 x π x r x (r + h) = 2 x π x 3 x (3 + 5) = 48 π ~ 150,8 cm²

Công thức và phương pháp tính thể tích hình trụ

Thể tích hình trụ là lượng không khí được cướp lưu giữ một hình trụ chắc chắn. Thể tích hình trụ dùng đơn vị chức năng đo là lập phương của khoảng cách (mũ 3 khoảng chừng cách).

1. Công thức tính thể tích hình trụ

V = π x r² x h

Trong đó:

- r: nửa đường kính hình trụ

- h: độ cao hình trụ

2. Ví dụ phương pháp tính thể tích của hình trụ

Ví dụ 1: Cho một lăng trụ ngẫu nhiên sở hữu nửa đường kính mặt mày lòng r = 4 centimet, trong lúc cơ, độ cao nối kể từ đỉnh của hình trụ xuống lòng hình trụ có tính nhiều năm h = 8 centimet. Hỏi thể tích của hình trụ này bởi vì bao nhiêu?

Hướng dẫn:

Công thức tính thể tích hình trụ: V = π x r² x h

Lời giải:

Theo cơ, tớ vận dụng vô công thức tính thể tích hình trụ và có: nửa đường kính mặt mày lòng hình trụ r = 4cm và độ cao hình trụ h = 8cm. Suy đi ra, tớ sở hữu công thức tính thể tích hình trụ như sau:

V = π x r² x h = π x 4² x 8 = ~ 402 cm³

Ví dụ 2: Một hình trụ sở hữu chu vi lòng bởi vì trăng tròn centimet, diện tích S xung xung quanh bởi vì 14 cm². Tính độ cao của hình trụ và thể tích của hình trụ.

Lời giải:

Diện tích xung xung quanh của hình trụ: Sxq = chu vi lòng x độ cao = 2 x π x r x h = trăng tròn x h = 14

→ h = 0,7 (cm)

Chu vi lòng bởi vì 20cm → 2 x π x r = trăng tròn → r ~ 3,18 cm

Thể tích của hình trụ: V = π x r² x h ~ 219,91 cm³

Ví dụ 3: Một hình trụ sở hữu diện tích S toàn phần cấp gấp đôi diện tích S xung xung quanh biết nửa đường kính lòng hình trụ là 6cm. Tính thể tích hình trụ.

Lời giải:

Xem thêm: Khái niệm, tính chất và công thức tính tỉ số lượng giác của góc nhọn

Diện tích toàn phần cấp gấp đôi diện tích S xung quanh: Stp = 2Sxq

→ 2 x 2 x π x r x h = 2 x π x r x (r + h) → 2h = 6 + h → h = 6 (cm)

Thể tích của hình trụ: V = π x r² x h ~ 678,58 cm³